专题4.1 指数与指数函数-2022-2023学年高一数学阶段性复习精选精练(人教A版2019必修第一册)
展开专题4.1 指数与指数函数
1.指数幂运算的一般原则
(1)有括号的先算括号里的,无括号的先做指数运算.
(2)先乘除后加减,负指数幂化成正指数幂的倒数.
(3)底数是负数,先确定符号;底数是小数,先化成分数;底数是带分数的,先化成假分数.
(4)若是根式,应化为分数指数幂,尽可能用幂的形式表示,运用指数幂的运算性质来解答.
(5)有理数指数幂的运算性质中,其底数都大于零,否则不能用性质来运算.
(6)将根式化为指数运算较为方便,对于计算的结果,不强求统一用什么形式来表示.如果有特殊要求,要根据要求写出结果.但结果不能同时含有根号和分数指数,也不能既有分母又含有负指数.
2.速记口诀
正数开方要分清,根指奇偶大不同,
根指为奇根一个,根指为偶双胞生.
负数只有奇次根,算术方根零或正,
正数若求偶次根,符号相反值相同.
负数开方要慎重,根指为奇才可行,
根指为偶无意义,零取方根仍为零.
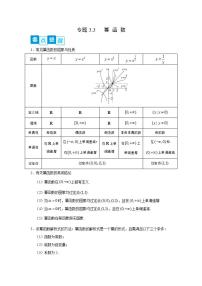
3.指数函数的图象与性质
图象
定义域
值域
奇偶性
非奇非偶函数
对称性
函数y=a−x与y=ax的图象关于y轴对称
过定点
过定点,即时,
单调性
在上是减函数
在上是增函数
函数值的变化情况
当时,;
当时,
当时,;
当时,
底数对图象的影响
指数函数在同一坐标系中的图象的相对位置与底数大小关系如下图所示,其中0
②在y轴左侧,图象从下到上相应的底数由大变小.
即无论在y轴的左侧还是右侧,底数按逆时针方向变大.
4.指数函数速记口诀:
指数增减要看清,抓住底数不放松;
反正底数大于0,不等于1已表明;
底数若是大于1,图象从下往上增;
底数0到1之间,图象从上往下减;
无论函数增和减,图象都过(0,1)点.
5.比较幂的大小的常用方法:
(1)对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;
(2)对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图象的变化规律来判断;
(3)对于底数不同,且指数也不同的幂的大小比较,可先化为同底的两个幂,或者通过中间值来比较.
6.解指数方程或不等式
简单的指数方程或不等式的求解问题.解决此类问题应利用指数函数的单调性,要特别注意底数a的取值范围,并在必要时进行分类讨论.
一、单选题
1.设,,如果函数满足,那么a的取值范围是
A. B.
C. D.
【答案】A
【分析】结合指数函数的单调性,时,函数单调递减, 时,函数单调递增.
即可判断结果.
【解析】因为函数为单调函数,且,故函数为单调递减函数,
那么.故选A
2.函数,且)恒过定点
A. B.
C. D.
【试题来源】四川省成都市蓉城名校联盟2021-2022学年高一上学期期中联考
【答案】C
【分析】利用指数函数恒过点即可求解.
【解析】当时, ,
所以函数恒过定点.故选C
3.已知,则f(3)等于
A. B.-
C. D.
【试题来源】四川省南充市阆中中学校2021-2022学年高一上学期期中
【答案】A
【分析】通过列方程进行求解即可.
【解析】令,因此有,故选A
4.在①;②;③;④;⑤中,y是关于x的指数函数的个数是
A.1 B.2
C.3 D.4
【试题来源】湘教版(2019) 必修第一册 突围者 第4章 第二节 指数函数
【答案】B
【分析】直接根据指数函数的定义依次判断即可.
【解析】根据指数函数的定义,知①⑤中的函数是指数函数,
②中底数不是常数,指数不是自变量,所以不是指数函数;
③中的系数是,所以不是指数函数;
④中底数,所以不是指数函数.故选B.
5.已知,则下列不等式成立的是
A. B.
C. D.
【试题来源】北京市丰台区2021-2022学年高一上学期期中数学练习试题(A卷)
【答案】A
【分析】根据指数函数的单调性,即可求出结果.
【解析】因为,所以;
又函数是上的增函数,所以.故选A.
6.已知函数(,且)的图象过定点,则
A. B.
C. D.
【试题来源】福建省福州第八中学2021-2022学年高一上学期期中考试
【答案】D
【分析】根据解析式,结合指数的性质易知过定点,结合已知即可求.
【解析】由解析式知,故过定点.
所以,则.故选D
7.已知函数、、、的大致图象如下图所示,则下列不等式一定成立的是
A. B.
C. D.
【试题来源】北京市十一学校2021-2022学年高一上学期期中考试
【答案】B
【分析】如图,作出直线得到,即得解.
【解析】如图,作出直线得到,
所以.故选B
8.设a>0,b>0,化简的结果是
A. B.
C. D.-3a
【试题来源】广东省佛山市南海区西樵高级中学2021-2022学年高一上学期中段考试
【答案】D
【分析】由分数指数幂的运算性质可得结果.
【解析】因为,,所以.故选D.
9.
A. B.
C. D.
【试题来源】福建省南平市浦城县2020-2021学年高二下学期第一次月考
【答案】C
【分析】根据给定条件利用指数幂的运算法则计算即得.
【解析】.故选C
10.下列计算正确的是
A. B.
C. D.
【试题来源】重庆复旦中学2021-2022学年高一上学期入学诊断
【答案】A
【分析】利用指数幂的运算求解判断.
【解析】A. 由指数幂的运算知,故正确;
B. 由指数幂的运算知,故错误;
C. ,故错误;
D. ,故错误.故选A
11.
A. B.5
C. D.25
【试题来源】2020-2021学年高一数学单元复习(沪教版2020必修第一册)
【答案】C
【分析】利用指数幂的运算性质求解即可
【解析】,故选C.
12.已知函数,,则下列等式不成立的是
A. B.
C. D.
【试题来源】新疆喀什第二中学2021-2022学年高一上学期期中考试
【答案】C
【分析】根据已知条件对选项逐一分析,由此确定正确选项.
【解析】,A成立.
,,B成立.
,C不成立.
,,D成立.
故选C
13.计算
A. B.
C. D.
【试题来源】吉林省长春市榆树市第一高级中学校2021-2022学年高一上学期期中
【答案】D
【分析】根据指数幂之间的运算即可.
【解析】,故选D.
14.若,,给出下列式子:①;②;③;④.其中恒有意义的个数是
A.1 B.2
C.3 D.4
【试题来源】湘教版(2019) 必修第一册 突围者 第4章 第一节 课时1 有理数指数幂、无理数指数幂
【答案】B
【分析】根据根式的意义逐个分析判断即可
【解析】根据根指数是偶数时,被开方数为非负数,可知②无意义;
当时,,此时④无意义.
因为,所以恒有意义,
因为任何数都可以开奇次方,所以恒有意义,
所以恒有意义的式子是①③.故选B.
15.计算的结果是
A. B.
C. D.
【试题来源】天津市南开区南大奥宇培训学校2021-2022学年高一上学期摸底考试
【答案】D
【分析】利用指数幂的运算求解.
【解析】因为,故选D
16.已知函数的图象如图所示,则函数的图象可能是
A. B. C. D.
【试题来源】广东省广州市铁一中学2021-2022学年高一上学期期中复习
【答案】B
【分析】由函数的图象可得,,从而可得的大致图象.
【解析】由的图象可得,,所以,,
故函数为增函数,相对向下平移大于1个单位,故选B.
17.已知函数的值域是
A. B.
C. D.
【试题来源】浙江省嘉兴市南湖片区2021-2022学年高一上学期期中检测
【答案】B
【分析】由于,进而得,即函数的值域是
【解析】因为,所以,
所以函数的值域是故选B
18.设,则的大小关系正确的是
A. B.
C. D.
【试题来源】湖南省长沙市第一中学2021-2022学年高一上学期期中
【答案】A
【分析】结合函数的单调性确定正确选项.
【解析】函数在上递减,所以.
函数在上递减,所以,所以.故选A
19.函数是指数函数,则有
A.或 B.
C. D.,且
【试题来源】湘教版(2019) 必修第一册 突围者 第4章 第二节 指数函数
【答案】C
【分析】根据指数函数定义得到,排除的情况得到答案.
【解析】由指数函数的概念得,解得或.
当时,底数是1,不符合题意,舍去;当时,符合题意.故选C.
20.若,,,则
A. B.
C. D.
【试题来源】广东省广州市奥林匹克中学和第八十九中学2021-2022学年高一上学期期中联合考试
【答案】A
【分析】根据指数函数的单调性判断a,b,c的大小关系即可.
【解析】由指数函数单调性知, ,即
又,即,故,故选A.
21.函数的图象向右平移个单位长度,所得图象与曲线关于轴对称,则
A. B.
C. D.
【试题来源】北京市第十四中学2022解高三上学期期中考试
【答案】C
【分析】根据函数图象变换关系,利用逆推法进行求解即可.
【解析】关于轴对称的函数为,即,
然后向左平移一个单位得到,
得,即,故选C.
22.已知,则
A. B.
C. D.
【试题来源】浙江省浙北G2(湖州中学、嘉兴一中)2021-2022学年高一上学期期中联考
【答案】B
【分析】根据指数函数和幂函数的单调性判断.
【解析】在上是增函数,是增函数,
所以,即.故选B.
23.已知f(x)=a-x(a>0,且a≠1),且f(-2)>f(-3),则a的取值范围是
A.a>0 B.a>1
C.a<1 D.0
【答案】D
【分析】根据指数函数的单调性可求.
【解析】因为f(-2)=a2, f(-3)=a3.
f(-2)>f(-3),即a2>a3,故0
A. B.
C. D.
【试题来源】北京市丰台区2021-2022学年高一上学期数学期中练习试题(B卷)
【答案】D
【分析】利用特殊值判断A、B,根据指数函数的性质判断C,根据幂函数的性质判断D;
【解析】因为,对于A,当,时,满足,但是,故A错误;
对于B:当时,,故B错误;
对于C:因为在定义域上单调递减,因为,所以,故C错误;
对于D:因为在定义域上单调递增,因为,所以,故D正确;故选D
25.已知,,,则
A. B.
C. D.
【试题来源】广东省广州市十三中2021-2022学年高一上学期期中
【答案】A
【分析】因为,,均为正数,先把与都6次方,化为整数,比较出大小,再比较,的大小,化为同底数幂,比较指数,利用指数函数的单调性即可比较.
【解析】因为,,均为正数,所以与都6次方得
,,8<9,所以,即
因为,,而是增函数,所以,即,
所以,故选A
26.设,,,则a,b,c的大小关系是
A. B.
C. D.
【试题来源】山西省怀仁市2021-2022学年高一上学期期中
【答案】C
【分析】利用指数函数的单调性及幂函数的单调性即可比较大小.
【解析】令,该函数为减函数
所以,即
令,该函数在上单调递增
所以,即
所以a,b,c的大小关系是故选C.
27.在某个时期,某湖泊中的蓝藻每天以的增长率呈指数增长,已知经过天以后,该湖泊的蓝藻数大约为原来的倍,那么经过天后该湖泊的蓝藻数大约为原来的
A.18倍 B.倍
C.倍 D.倍
【试题来源】广东省深圳市2020-2021学年高一下学期期末
【答案】C
【分析】构造指数函数模型,计算即可.
【解析】某湖泊中的蓝藻每天以的增长率呈指数增长,经过30天以后,该湖泊的蓝藻数大约为原来的6倍,
设湖泊中原来蓝藻数量为,则,
经过60天后该湖泊的蓝藻数量为
经过60天后该湖泊的蓝藻数大约为原来的36倍.故选C.
28.已知函数(其中)的图象如图所示,则函数的图象是
A. B.
C. D.
【试题来源】广东省阳春市第一中学2022届高三上学期10月月考
【答案】A
【分析】根据二次函数图象上特殊点的正负性,结合指数型函数的性质进行判断即可.
【解析】由图象可知,因为,所以由可得,由可得,由可得,
因此有,所以函数是减函数,,所以选项A符合,故选A
29.设是非零实数,已知,则
A. B.
C.2 D.3
【试题来源】江苏省南京市南师附中、秦淮科技高中2020-2021学年高一上学期联考
【答案】A
【分析】根据,利用完全平方公式和平方差公式分别求得, , ,代入求解.
【解析】因为,
所以,
所以 ,,
所以,
,
,故选A
30.要得到函数的图象,只需将函数的图象
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
【试题来源】黑龙江省哈尔滨市第三中学2021-2022学年高三上学期第一次验收考试
【答案】B
【分析】化简整理,可得,根据平移变换的原则,即可得答案.
【解析】由题意得,
所以只需将函数的图象向右平移个单位,即可得到的图象.故选B
31.设,都是正整数,且,若,则不正确的是
A. B.
C. D.
【试题来源】安徽省安庆市九一六学校2020-2021学年高二下学期5月月考
【答案】C
【分析】根据指数幂与根式的转化和运算判断.
【解析】因为,都是正整数,且,若,则:
A. ,故正确;
B. ,故正确;
C. ,故错误;
D. 任意非零数的0次幂都是1,故正确.故选C
32.已知,,化简得
A. B.
C. D.
【试题来源】江苏省南通市如东高级中学2021-2022学年高一上学期10月阶段测试一
【答案】B
【分析】根据根式和实数指数幂的运算法则,即得解
【解析】由题意:,
,故选B
33.如图是指数函数①,②,③,④的图象,则a,b,c,d与0和1的大小关系是
A. B.
C. D.
【试题来源】宁夏中宁中学2021-2022学年高一上学期期中考试
【答案】B
【分析】根据指数函数的单调性分析得到,大于1,,大于0小于1,再通过取得到具体的大小关系.
【解析】当底数大于1时指数函数是定义域内的增函数,
当底数大于0小于1时是定义域内的减函数,
由图可知,大于1,,大于0小于1.
又由图可知,即.,即.
,,,与1的大小关系是.故选.
34.当生物死亡后,它机体内原有的碳14会按确定的规律衰减.按照惯例,人们将每克组织的碳14含量作为一个单位,大约每经过5730年一个单位的碳14衰减为原来的一半,这个时间称为“半衰期”.当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就测不到碳14了.如果用一般的放射性探测器不能测到碳14,那么死亡生物组织内的碳14至少经过了( )个“半衰期”.(提示:)
A.10 B.9
C.11 D.8
【试题来源】江苏省南京市人民中学2021-2022学年高一上学期10月月考
【答案】A
【分析】根据题意,结合指数不等式与参考数据,即可求解.
【解析】由题意可设生物组织内原有的碳14含量为x,需要经过n个才能被测到碳14,
则,即,
由参考数据可知,,,
所以.故选A.
35.已知是偶函数,且当时,若,则
A. B.
C. D.
【试题来源】河南省焦作市普通高中2021-2022学年高一上学期期中考试
【答案】B
【分析】根据函数奇偶性的性质,进行转化,建立方程进行求解即可.
【解析】是偶函数,且当当时.若,
,故选B
36.若,则的值为
A. B.
C. D.
【试题来源】四川省成都市蓉城名校联盟2021-2022学年高一上学期期中联考
【答案】B
【分析】已知等式平方后可得结论.
【解析】因为,所以,
所以,故选B.
37.函数的值域为
A. B.
C. D.
【试题来源】江西省赣州市十六县(市)十七校2022届高三上学期期中联考
【答案】B
【分析】把作为一个整体,求出其范围,再利用基本不等式求解.
【解析】由已知,
当且仅当,即时等号成立,
所以的值域是.故选B.
38.若,,,则
A. B.
C. D.
【试题来源】广西桂林普通高中2022届高三1月教学质量检测
【答案】B
【分析】先化简,,,再根据指数函数的单调性比较大小即可得答案.
【解析】因为,,
因为函数在上单调递增,,
所以,
另一方面指数函数在上单调递增,
所以,
所以,故选B
39.已知,则下列运算中正确的是
A. B.
C. D.
【试题来源】江苏省南京航空航天大学附属中学2020-2021学年高一上学期10月月考
【答案】B
【分析】由,,即可求得,从而判断A;
由,,即可求得,从而判断B;
由,可求得,再由,即可求得,从而判断C;
由,即可求得,从而判断D.
【解析】A选项:,
所以,
又,
所以,
所以,
故A错误;
B选项:,
所以,故B正确;
C选项:,,,
,
,故C错误;
D选项:,
故D错误,故选B.
40.已知,,则与之间的大小关系是
A. B.
C. D.无法比较
【试题来源】河南省焦作市温县第一高级中学2021-2022学年高一上学期10月月考
【答案】B
【分析】构造函数,得到,然后利用不等式的性质,由与的大小判断.
【解析】设,则,
所以,
,
而,
所以,即,故选B
二、多选题
1.下列各式错误的是
A.=-3 B.=a
C.=2 D.=2
【试题来源】海南省白沙黎族自治县白沙中学2020-2021学年高一下学期期中考试
【答案】ABD
【分析】由根式、指数幂的运算性质求各选项的值即可.
【解析】A:=3,错误;
B:,错误;
C:,正确;
D:,错误.
故选ABD
2.已知函数且,的图象不经过第三象限,则的范围可能为
A., B.,
C., D.,
【试题来源】重庆市第八中学2021-2022学年高一艺术班上学期期中
【答案】ABC
【分析】指数函数图象问题,对和进行讨论.
【解析】若,函数图象如图所示
要想图象不经过第三象限,则需要向上平移,
或向下平移不超过1个单位长度,故或,
解得或,故AB正确;
若,函数图象如图所示
要想图象不经过第三象限,则需要向上平移,故,解得,即C正确,D错误.故选ABC
3.已知函数的图象恒过点,则下列函数图象也过点的是
A. B.
C. D.
【试题来源】福建省厦门外国语学校2021-2022学年高一上学期线上教学摸底测试
【答案】ABC
【分析】令求得图象恒过点A的坐标,再验证选项中的函数是否过点A.
【解析】函数中,令,解得,,
所以的图象恒过点A(1,2),
对于A,时,,则函数图象过点A;
对于B,时,,则函数图象过点A;
对于C,时,,则函数图象过点A;
对于D,时,, 则函数图象不过点A.
故选ABC
4.将一条均匀柔软的链条两端固定,在重力的作用下它所呈现的形状叫悬链线,例如悬索桥等.建立适当的直角坐标系,可以写出悬链线的函数解析式为,其中a为悬链线系数,称为双曲余弦函数,其函数表达式为,相应地双曲正弦函数的函数表达式为.下列判断正确的有
A. B.
C. D.
【试题来源】福建省福州市第一中学2020-2021学年高二下学期期末
【答案】ABD
【分析】对求导即可判断A;利用双曲正余弦函数的性质,应用指数幂的运算求、、、、判断B、C、D的正误.
【解析】A:,正确;
B:
,正确;
C:
,错误;
D:,而
,正确.
故选ABD
5.已知函数,实数、满足,则下列结论正确的有
A. B.、,使
C. D.
【试题来源】山东省新泰市第一中学东校2021-2022学年高三上学期第一次月考
【答案】CD
【分析】作出函数的图象,利用绝对值的性质可得出,可判断AC选项的正误,利用基本不等式可判断BD选项的正误.
【解析】画出函数的图象如下图所示:
当时,,则,
设,则,
因为,可得,可得,
由,可得,可得,
由,可得,则,A错,C对;
由基本不等式可得,所以,则,B错,D对.
故选CD.
三、填空题
1.当时,函数的值域是____________.
【试题来源】宁夏中宁中学2021-2022学年高一上学期期中考试
【答案】
【分析】根据指数函数的单调性求解.
【解析】是增函数,时,,即,值域为.
故答案为.
2.函数恒过定点____________.
【试题来源】广东实验中学2021-2022学年高一上学期期中
【答案】
【分析】由恒成立可得定点坐标.
【解析】,恒过定点.
故答案为.
3.____________.
【试题来源】北京市丰台区2021-2022学年高一上学期数学期中练习试题(B卷)
【答案】5
【分析】应用有理数指数幂的运算性质化简求值即可.
【解析】.
故答案为5
4.计算:____________.
【试题来源】北京市丰台区2021-2022学年高一上学期期中数学练习试题(A卷)
【答案】4
【分析】根据指数幂的运算法则可计算.
【解析】.
故答案为4.
5.____________.
【试题来源】云南大学附属中学星耀学校2021-2022学年高一上学期期中考试
【答案】0
【分析】利用根式和分数指数幂的运算性质直接求解即可
【解析】
,
故答案为0
6.已知a2x=2(a>0),则=___________.
【试题来源】上海市普陀区桃浦中学2021-2022学年高一上学期期中
【答案】
【分析】由可得,根据对原式化简计算即可.
【解析】由,得,所以,
则.
故答案为.
7.函数且的图象恒过定点,则____________.
【试题来源】重庆市第八中学2021-2022学年高一艺术班上学期期中
【答案】
【分析】指数函数(且)恒过点 再此基础上求解题干中的函数经过的定点
【解析】,令得,且当时,,所以恒过定点,所以,,所以
故答案为
8.2018年5月至2019年春,在阿拉伯半岛和伊朗西南部,沙漠蝗虫迅速繁衍,呈指数增长,引发了蝗灾.到2020年春季,蝗灾已波及印度和巴基斯坦.假设蝗虫的日增长率为,最初有只,则经过152天后约达到最初的____________倍(参考数据:).
【试题来源】湘教版(2019) 必修第一册 突围者 第4章 第二节 指数函数
【答案】1681
【分析】由题设可得x天后蝗虫的数量,则152天后约达到最初的倍,利用指数的运算性质求值即可.
【解析】依题意知经过x天后蝗虫的数量为,
所以经过152天后蝗虫的数量为,
又,
所以经过152天后约达到最初的1681倍.
故答案为
9.若且,则函数的图象恒过的定点的坐标为____________.
【试题来源】湘教版(2019) 必修第一册 突围者 第4章 第二节 指数函数
【答案】
【分析】令,得,计算,得到答案.
【解析】令,得,所以,
所以函数的图象恒过定点.
故答案为.
10.函数在上单调____________(填“递增”或“递减”).
【试题来源】湘教版(2019) 必修第一册 突围者 第4章 第二节 指数函数
【答案】递减
【分析】将原函数看成含的二次型复合函数,利用指数函数、二次函数的性质,结合复合函数的单调性判断区间单调性即可.
【解析】由题知.令,则,
因为在上单调递增,在上单调递减,
所以函数在上单调递减.
故答案为递减
11.下列说法中:
①函数与函数的图象关于轴对称;
②函数(且)的图象恒过点;
③函数的最大值为1;
④任取,都有.
所有正确的命题序号为____________.
【试题来源】宁夏固原市五原中学补习部2022届高三上学期期中考试
【答案】①②③
【分析】利用函数的单调性,对称性和奇偶性,结合各项的描述判断正误.
【解析】①:在同一坐标系中,对于与:当x值相同时y值互为相反数,即它们关于轴对称,正确;
②:函数(且)的图象,当时,故函数过定点,正确;
③:由为偶函数,由有且递减 ,结合偶函数的对称性知时且递增,故函数的最大值为1,正确;
④:当有,错误;
故答案为①②③
12.已知常数且,若无论取何值,函数(、为实数)的图象过定点,则的值为____________.
【试题来源】上海市建平中学2020-2021学年高一上学期期中
【答案】3
【分析】函数过定点得到,得到答案.
【解析】,当时,,故函数过定点,
即,.
故答案为3.
13.化简(其中a>0,b>0)=____________.
【试题来源】上海市普陀区甘泉外国语中学2021-2022学年高一上学期期中
【答案】
【分析】利用指数幂的运算法则即得.
【解析】因为.
故答案为.
14.计算:____________.
【试题来源】浙江省浙北G2(湖州中学、嘉兴一中)2021-2022学年高一上学期期中联考
【答案】
【分析】根据幂的运算法则,根式的定义计算.
【解析】.
故答案为.
15.给定正实数,化简代数式____________.
【试题来源】上海市上海中学2021-2022学年高一上学期期中
【答案】
【分析】直接根据指数幂的运算性质计算即可.
【解析】.
故答案为
16.计算(式中字母均是正数):
=____________.
【试题来源】云南省昆明市第一中学2021-2022年高一上学期期中考
【答案】
【分析】根据指数的运算性质即可算出答案.
【解析】原式=
故答案为
17.____________.
【试题来源】重庆市第七中学2021-2022学年高一上学期期中
【答案】
【分析】根据指数的运算性质,直接计算即可
【解析】
故答案为
18.已知函数,若其在区间上是增函数,则实数a,b应满足的条件为____________.
【试题来源】福建省福州第八中学2021-2022学年高一上学期期中考试
【答案】且.
【分析】设,利用复合函数的单调性分和两种情况讨论即得.
【解析】设,
当时,函数在区间上是增函数,即g(x)在区间上是增函数,
所以即;
当时,函数在区间上是增函数,即g(x)在区间上是减函数,但g(x)在区间上是增函数,
故不存在实数a,b使函数在区间上是增函数;
所以函数在区间上是增函数,实数a,b应满足的条件为且.
故答案为且.
四、解答题
1.已知函数(且)在上的最大值与最小值之和为20,记.
(1)求的值;
(2)证明:;
(3)求的值.
【试题来源】海南省海口市第一中学2021-2022学年高一上学期期中考试
【答案】(1)
(2)证明见解析.
(3)
【分析】(1)根据的单调性,结合已知条件可得,即可求的值;
(2)由(1)分别写出、的解析式,进而应用指数运算性质化简即可证结论.
(3)根据(2)的结论求值即可.
【解析】(1)因为为单调函数,
所以上的最大值与最小值之和为,又且,
所以.
(2)由(1)知,则,
所以,得证.
(3)由(2)知
所以.
2.已知指数函数(且)经过点.
(1)求的解析式及的值;
(2)若,求x的取值范围.
【试题来源】陕西省宝鸡市陈仓区2021-2022学年高一上学期期中
【答案】(1),
(2)
【分析】(1)将点代入到,解得a的值,即可求出解析式,由此可求出的值;
(2)根据指数函数为增函数,转化为不等式,解之即可.
【解析】(1)因为(且)经过点,
所以,所以,
所以,
所以;
(2)因为,即,
又在R上为增函数,
所以,
所以x的取值范围为.
3.已知函数(且)的图象经过点.
(1)求函数的解析式;
(2)求函数的值域.
【试题来源】云南省昆明市第一中学2021-2022年高一上学期期中考
【答案】(1)
(2)
【分析】(1)利用待定系数法,将代入即可得到解析式
(2)可先确定的范围,再确定由指数函数的性质确定的范围
【解析】(1)由已知得,解得,
所以函数的解析式为
(2)令
因为,所以,
所以,
故的值域是.
4.已知函数是定义在上的奇函数,且函数是定义在上的偶函数.
(1)求函数的解析式;
(2)当时,求的取值范围.
【试题来源】山西省怀仁市2021-2022学年高一上学期期中
【答案】(1)
(2)
【分析】(1)对中的换为,再根据奇偶性得到,即可求出;
(2)由(1)知,,即,令,则原不等式转化为,再解一元二次不等式求出的取值范围,再根据对勾函数的性质计算可得;
【解析】(1)因为是定义在上的偶函数,
所以,即,
因为是定义在上的奇函数,所以,
所以,所以;
(2)由(1)知,,得,
即,令,,则,解得,
所以,
令,,所以
在,为减函数,所以,
所以的取值范围为.
5.已知函数(其中,为常数,且)的图象经过点.
(1)求函数的解析式;
(2)若不等式在区间上恒成立,求实数的取值范围.
【试题来源】河南省南阳市2021-2022学年高一上学期期中考试
【答案】(1)
(2)
【分析】(1)代入点,待定系数即得解;
(2)代入后参变分离可得,结合的单调性,即得解
【解析】(1)由题意得,,;
(2)由(1)知在区间上恒成立,
即在区间上恒成立
设,因为在上单调递减,
故,所以实数的取值范围为.
高中数学人教A版 (2019)必修 第一册4.1 指数课时作业: 这是一份高中数学人教A版 (2019)必修 第一册4.1 指数课时作业,文件包含专题41指数解析版docx、专题41指数原卷版docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.1 指数同步达标检测题: 这是一份高中数学人教A版 (2019)必修 第一册4.1 指数同步达标检测题,文件包含专题41指数与指数函数解析版docx、专题41指数与指数函数原卷版docx等2份试卷配套教学资源,其中试卷共47页, 欢迎下载使用。
专题4.1 指数- 2022-2023学年高一数学阶段性复习精选精练(人教A版2019必修第一册): 这是一份专题4.1 指数- 2022-2023学年高一数学阶段性复习精选精练(人教A版2019必修第一册),文件包含专题41指数解析版docx、专题41指数原卷版docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。