2022年中考数学真题汇编：函数基础知识(含解析)

2022数学中考试题汇编函数基础知识

一、选择题

1. (2022·广东省云浮市 )水中涟漪圆形水波不断扩大，记它的半径为，则圆周长与的关系式为下列判断正确的是(    )

A. 是变量 B. 是变量 C. 是变量 D. 是常量

2. (2022·山东省 )某地区用电量与应缴电费之间的关系如下表：则下列叙述错误的是(    )

A. 若所缴电费为元，则用电量为千瓦时
B. 若用电量为千瓦时，则应缴电费元
C. 用电量每增加千瓦时，电费增加元
D. 设用电量千瓦时，应缴电费为元，则和满足

3. (2022·山东省 )在实验课上，小亮利用同一块木板测得小车从不同高度与下滑的时间的关系如下表：

下列结论错误的是

A. 当时，约秒
B. 随高度增加，下滑时间越来越短
C. 估计当时，一定小于秒
D. 高度每增加了，时间就会减少秒

4. (2022·北京市 )下面的三个问题中都有两个变量：
   汽车从地匀速行驶到地，汽车的剩余路程与行驶时间；
   将水箱中的水匀速放出，直至放完，水箱中的剩余水量与放水时间；
   用长度一定的绳子围成一个矩形，矩形的面积与一边长．
   其中，变量与变量之间的函数关系可以用如图所示的图象表示的是(    )

A.  B.  C.  D.

5. (2022·江苏省常州市 )某城市市区人口万人，市区绿地面积万平方米，平均每人拥有绿地平方米，则与之间的函数表达式为(    )

A.  B.  C.  D.

6. (2022·江苏省连云港市 )函数中自变量的取值范围是(    )

A.  B.  C.  D.

7. (2022·湖北省恩施土家族苗族自治州 )函数的自变量的取值范围是(    )

A.  B.  C. 且 D.

8. (2022·重庆市 )如图，曲线表示一只蝴蝶在飞行过程中离地面的高度随飞行时间的变化情况，则这只蝴蝶飞行的最高高度约为(    )

A.  B.  C.  D.

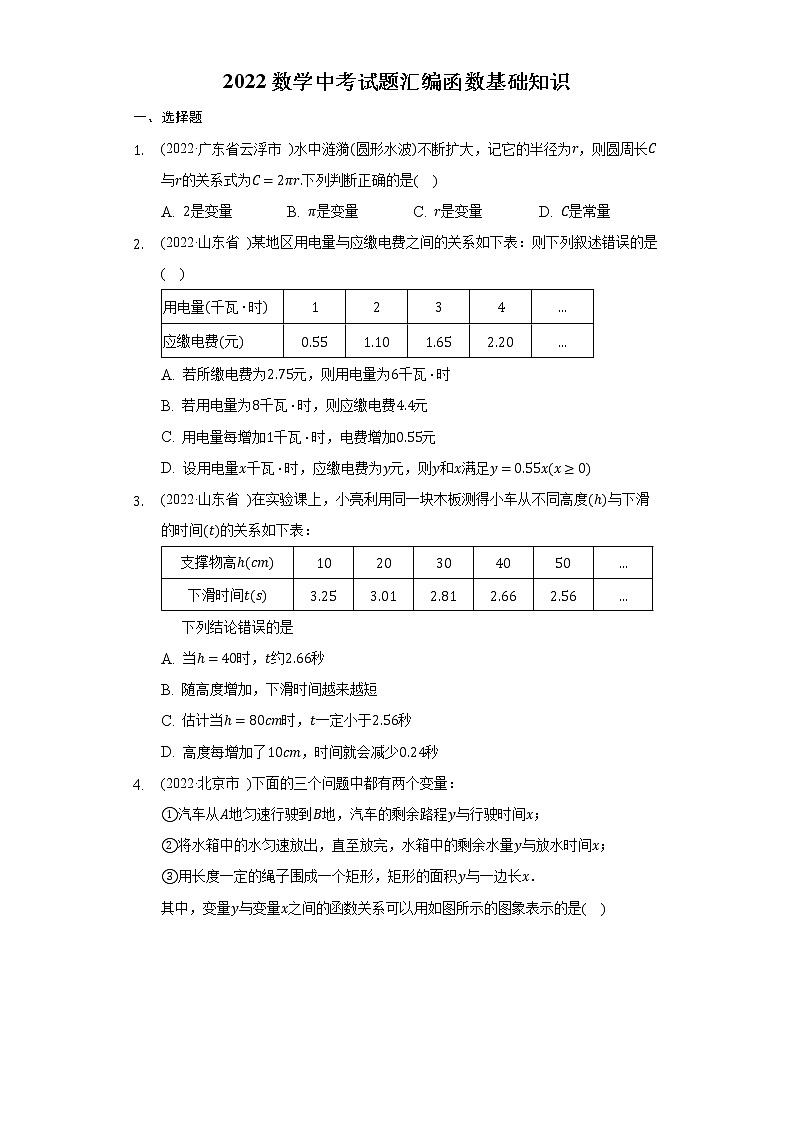
9. (2022·山东省烟台市 )周末，父子二人在一段笔直的跑道上练习竞走，两人分别从跑道两端开始往返练习．在同一直角坐标系中，父子二人离同一端的距离米与时间秒的关系图象如图所示．若不计转向时间，按照这一速度练习分钟，迎面相遇的次数为(    )

A.  B.  C.  D.

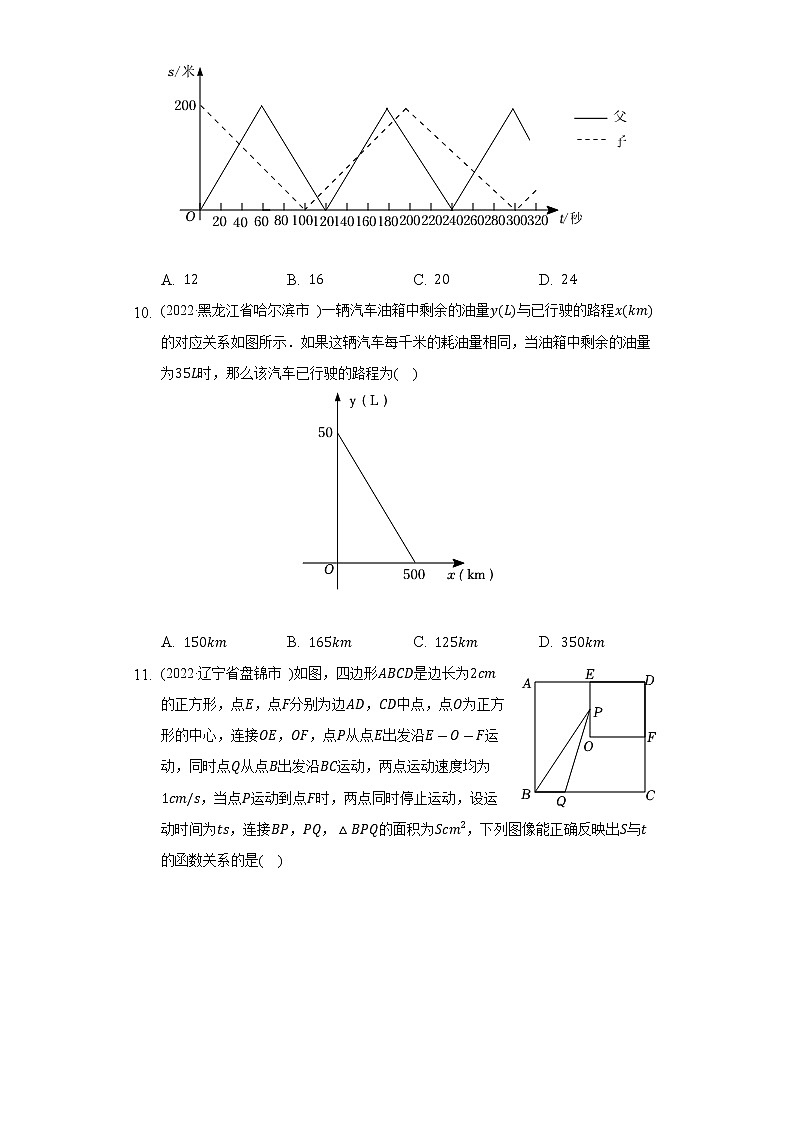
10. (2022·黑龙江省哈尔滨市 )一辆汽车油箱中剩余的油量与已行驶的路程的对应关系如图所示．如果这辆汽车每千米的耗油量相同，当油箱中剩余的油量为时，那么该汽车已行驶的路程为(    )

A.  B.  C.  D.

11. (2022·辽宁省盘锦市 )如图，四边形是边长为的正方形，点，点分别为边，中点，点为正方形的中心，连接，，点从点出发沿运动，同时点从点出发沿运动，两点运动速度均为，当点运动到点时，两点同时停止运动，设运动时间为，连接，，的面积为，下列图像能正确反映出与的函数关系的是(    )

A.  B.
C.  D.

12. (2022·贵州省铜仁市 )如图，等边、等边的边长分别为和开始时点与点重合，在上，在上，沿向右平移，当点到达点时停止．在此过程中，设、重合部分的面积为，移动的距离为，则与的函数图象大致为(    )

A.  B.
C.  D.

13. (2022·黑龙江省齐齐哈尔市 )如图所示图中各角均为直角，动点从点出发，以每秒个单位长度的速度沿路线匀速运动，的面积随点运动的时间秒之间的函数关系图象如图所示，下列说法正确的是(    )

A.  B.  C.  D.

14. (2022·辽宁省盘锦市 )如图，四边形是正方形，，点为射线上一点，连接，将绕点顺时针旋转得到线段，过作平行线交延长线于设长为，四边形的面积为，下列图象能正确反映出与函数关系的是(    )

A.  B.
C.  D.

15. (2022·甘肃省临夏回族自治州 )如图，在菱形中，，动点从点出发，沿折线方向匀速运动，运动到点停止．设点的运动路程为，的面积为，与的函数图象如图所示，则的长为(    )

A.  B.  C.  D.

16. (2022·辽宁省铁岭市 )如图，在等边三角形中，，在中，，，，点，，，在一条直线上，点，重合，沿射线方向运动，当点与点重合时停止运动．设运动的路程为，与重叠部分的面积为，则能反映与之间函数关系的图象是(    )

A.  B.
C.  D.

二、填空题

17. (2022·山东省 )汽车离开甲站后，以的速度匀速前进了，则汽车离开甲站所走的路程与时间之间的关系式是______．
18. (2022·黑龙江省哈尔滨市 )在函数中，自变量的取值范围是______．
19. (2022·湖南省娄底市 )函数的自变量的取值范围是______．
20. (2022·内蒙古自治区赤峰市 )已知王强家、体育场、学校在同一直线上，下面的图像反映的过程是：某天早晨，王强从家跑步去体育场锻炼，锻炼结束后，步行回家吃早餐，饭后骑自行车到学校．图中表示时间，表示王强离家的距离．则下列结论正确的是______填写所有正确结论的序号
    体育场离王强家
    王强在体育场锻炼了
    王强吃早餐用了
    王强骑自行车的平均速度是

21. (2022·辽宁省营口市 )如图，在四边形中，，，，动点，同时从点出发，点以的速度沿向点运动运动到点即停止，点以的速度沿折线向终点运动，设点的运动时间为，的面积为，若与之间的函数关系的图象如图所示，当时，则______．

22. (2022·湖北省咸宁市 )如图，在中，，动点从点出发，沿折线匀速运动至点停止．若点的运动速度为，设点的运动时间为，的长度为，与的函数图象如图所示．当恰好平分时的值为______．

三、计算题

23. (2022·四川省雅安市 )某商场购进，两种商品，已知购进件商品和件商品费用相同，购进件商品和件商品总费用为元．
    求，两种商品每件进价各为多少元？列方程或方程组求解
    若该商场计划购进，两种商品共件，其中商品件．若商品按每件元销售，商品按每件元销售，求销售完，两种商品后获得总利润元与件的函数关系式．
24. (2022·山东省 )阅读理解：
    下面的图象表示的个位数字随为正整数变化的规律．请解答下列问题：
    
    根据图象回答下列问题：
    当为正整数时，的个位数字是______；
    当为正整数时，的个位数字是______；
    当为正整数时，的个位数字是______；
    当为正整数时，的个位数字是______；
    求：的个位数字．
    解：
    ．
    因为，所以由得，的个位数字是，即的个位数字是．
    类比应用：
    求：的个位数字．

四、解答题

25. (2022·广东省云浮市 )物理实验证实：在弹性限度内，某弹簧长度与所挂物体质量满足函数关系下表是测量物体质量时，该弹簧长度与所挂物体质量的数量关系．

求与的函数关系式；
当弹簧长度为时，求所挂物体的质量．

26. (2022·湖北省鄂州市 )在“看图说故事”活动中，某学习小组设计了一个问题情境：小明从家跑步去体育场，在那里锻炼了一阵后又走到文具店买圆规，然后散步走回家．小明离家的距离与他所用的时间的关系如图所示：
    小明家离体育场的距离为______，小明跑步的平均速度为______；
    当时，请直接写出关于的函数表达式；
    当小明离家时，求他离开家所用的时间．

27. (2022·浙江省嘉兴市 )月日，某港口的湖水高度和时间的部分数据及函数图象如下：

数据来自某海洋研究所数学活动：
根据表中数据，通过描点、连线光滑曲线的方式补全该函数的图象．
观察函数图象，当时，的值为多少？当的值最大时，的值为多少？
数学思考：
请结合函数图象，写出该函数的两条性质或结论．
数学应用：
根据研究，当潮水高度超过时，货轮能够安全进出该港口．请问当天什么时间段适合货轮进出此港口？

28. (2022·山东省 )如图，圆柱的高是，当圆柱的底面半径由小到大变化时，圆柱的体积也随之发生了变化．
    在这个变化中，自变量是______，因变量是______；
    写出体积与半径的关系式；
    当底面半径由到变化时，通过计算说明圆柱的体积增加了多少．

参考答案

1.【答案】 

【解析】解：根据题意可得，
在中．，为常量，是自变量，是因变量．
故选：．
2.【答案】 

【解析】解：若所缴电费为元，则用电量为千瓦时，故本选项错误；
B.若用电量为千瓦时，则应缴电费元，故本选项正确；
C.用电量每增加千瓦时，电费增加元，故本选项正确；
D.所缴电费和用电量之间满足，故本选项正确；
故选：．
3.【答案】 

【解析】

解：当时，约秒，故A正确；
B.高度从增加到，而时间却从减少到，故B正确；
C.根据中的估计，当时，一定小于秒，故C正确；
D.错误，因为时间的减少是不均匀的；
故选D．  

4.【答案】 

【解析】解：汽车从地匀速行驶到地，根据汽车的剩余路程随行驶时间的增加而减小，故符合题意；
将水箱中的水匀速放出，直至放完，根据水箱中的剩余水量随放水时间的增大而减小，故符合题意；
用长度一定的绳子围成一个矩形，周长一定时，矩形面积是长的二次函数，故不符合题意；
所以变量与变量之间的函数关系可以用如图所示的图象表示的是．
故选：．
5.【答案】 

【解析】解：由城市市区人口万人，市区绿地面积万平方米，
则平均每人拥有绿地．
故选：．
6.【答案】 

【解析】解：，
．
故选：．
7.【答案】 

【解析】解：由题意得：
，
解得：且．
故选：．
8.【答案】 

【解析】解：观察图象，当时，，
这只蝴蝶飞行的最高高度约为，
故选：．
9.【答案】 

【解析】解：由图可知，父子速度分别为：米秒和米秒，
分钟父子所走路程和为米，
父子二人第一次迎面相遇时，两人所跑路程之和为米，
父子二人第二次迎面相遇时，两人所跑路程之和为米，
父子二人第三次迎面相遇时，两人所跑路程之和为米，
父子二人第四次迎面相遇时，两人所跑路程之和为米，

父子二人第次迎面相遇时，两人所跑路程之和为米，
令，
解得，
父子二人迎面相遇的次数为，
故选：．
10.【答案】 

【解析】解：当油箱中剩余的油量为时，那么该汽车已行驶的路程为：，
故选：．
11.【答案】 

【解析】解：当时，
正方形的边长为，点为正方形的中心，
直线垂直，
点到直线的距离为，，
；
当时，
正方形的边长为，点分别为边，中点，点为正方形的中心，
直线，
点到直线的距离为，，
；
故选D．
12.【答案】 

【解析】解：如图所示，当和重合时，，

当移动的距离为时，在内，，
当在的右边时，如图所示，设移动过程中与交于点，过点坐垂直于，垂足为，

根据题意得，，
，
，，
是等边三角形，
，
，
，
，
，
，
，
当时，是一个关于的二次函数，且开口向上，
当时，，当时，，
故选：．
13.【答案】 

【解析】解：由图的第一段折线可知：点经过秒到达点处，此时的三角形的面积为，
动点从点出发，以每秒个单位长度的速度沿路线匀速运动，
．
，
，
选项不正确，选项也不正确；
由图的第二段折线可知：点再经过秒到达点处，
，
由图的第三段折线可知：点再经过秒到达点处，
，
由图的第四段折线可知：点再经过秒到达点处，
．
选项不正确；
图中各角均为直角，
，
选项的结论正确，
故选：．
14.【答案】 

【解析】解：方法一：由题意知，当点在点右侧时，越大，则则四边形的面积越大，
故D选项符合题意；
方法二：如下图，当点在之间时，作于，

，
，
，
，
在和中，
，
≌，
，，
，
四边形的面积，
同理可得当点在点右侧时，，

四边形的面积，
综上所述，当时，函数图象为开口方向向下的抛物线，当时，函数图象为开口方向向上的抛物线，
故选：．
方法一：根据点在点右侧时，越大，则四边形的面积越大，即可以得出只有选项符合要求；
方法二：分两种情况分别求出与的关系式，根据的取值判断函数图象即可．
本题主要考查二次函数图象的性质，熟练根据题意列出函数关系式是解题的关键．

15.【答案】 

【解析】解：在菱形中，，
为等边三角形，
设，由图可知，的面积为，
的面积，
解得：，
故选：．
16.【答案】 

【解析】解：过点作，交于点，

在等边中，，
在中，，
，
，
，
在等边中，，
，，
，
当时，设与交于点，此时与重叠部分为，

由题意可得，
；
当时，设与交于点，此时与重叠部分为四边形，

由题意可得：，则，，
，
，
当时，设与交于点，过点作，交于点，
此时与重叠部分为，

由题意可得，则，，
，

在中，，
，
，
综上，选项A的图像符合题意，
故选：．
17.【答案】 

【解析】解：根据题意，得．
故答案为：．
18.【答案】 

【解析】解：由题意得：
，
，
故答案为：．
19.【答案】 

【解析】解：由题意得：
，
解得：，
故答案为：．
20.【答案】 

【解析】解：由图象中的折线中的第一段可知：王强家距离体育场千米，用时分钟跑步到达，
的结论正确；
由图象中的折线中的第一段可知：王强从第分钟开始锻炼，第分钟结束，
王强锻炼的时间为：分钟，
的结论不正确；
由图象中的折线中的第三段可知：王强从第中开始回家，第分钟到家；
由图象中的折线中的第四段可知：王强从第分钟开始吃早餐，第分钟结束，
王强吃早餐用时：分钟，
的结论正确；
由图象中的折线中的第四段可知：王强从第分钟开始骑车去往千米外的学校，第分钟到达学校，
王强骑自行车用时为：分钟，
王强骑自行车的平均速度是：
的结论正确．
综上，结论正确的有：，
故答案为：．
21.【答案】 

【解析】解：过点作，垂足为，

在中，
，，
，
点的速度为，点的速度为，
，，
，
在和中，
，，
∽，
点在上运动时，为等腰直角三角形，
，
当点在上运动时，，
由图像可知，当此时面积最大，或负值舍去，
，
当时，过点作于点，如图：

此时，
在中，，，
在中，，，
，，，
，
即，
当时，，
故答案为：．
22.【答案】 

【解析】解：如图，连接，

由图可得，
，，
，
平分，
，
，，
，
，，
∽，
，
，
，负值舍去，
，
故答案为：．
23.【答案】解：商品每件的进价为元，商品每件的进价为元，
根据题意得：．
解得：
答：商品每件的进价为元，商品每件的进价为元．
商品件，商品件，

． 

24.【答案】       

【解析】解：故答案为：；；；；








因为，所以的个位数字是，所以的个位数字是，
即的个位数字是．
25.【答案】解：把，代入中，
得，
解得：，
所以与的函数关系式为；
把代入中，
得，
解得：．
所挂物体的质量为． 

26.【答案】  

【解析】解：小明家离体育场的距离为，小明跑步的平均速度为；
故答案为：，；
如图，，，

设的解析式为：，
则，
解得：，
的解析式为：，
当时，关于的函数表达式为：；
当时，，
，
，
当小明离家时，他离开家所用的时间为或．
27.【答案】解：如图：

通过观察函数图象，当时，，当值最大时，；
该函数的两条性质如下答案不唯一：
当时，随的增大而增大；
当时，有最小值为；
由图象，当时，或或或，
当或时，，
即当或时，货轮进出此港口． 

28.【答案】   

【解析】解：在这个变化过程中，自变量是，因变量是．
故答案为：，；
圆柱的体积与底面半径的关系式是．

所以当底面半径由到变化时，通过计算说明圆柱的体积增加了．