高中数学湘教版（2019）选择性必修 第一册第2章 平面解析几何初步2.6 直线与圆、圆与圆的位置关系课堂教学课件ppt

这是一份高中数学湘教版（2019）选择性必修 第一册第2章 平面解析几何初步2.6 直线与圆、圆与圆的位置关系课堂教学课件ppt，文件包含261直线与圆的位置关系pptx、261直线与圆的位置关系DOCX等2份课件配套教学资源，其中PPT共46页， 欢迎下载使用。

1.掌握直线与圆的三种位置关系：相交、相切、相离.2.会用代数法和几何法来判定直线与圆的三种位置关系.
通过直线与圆的位置关系的判断及应用，发展学生的逻辑推理、数学抽象及数学运算素养.
课前预习教材必备知识探究
课堂研析题型关键能力提升
课后分层精练核心素养达成
ＫＥＱＩＡＮＹＵＸＩＪＩＡＯＣＡＩＢＩＢＥＩＺＨＩＳＨＩＴＡＮＪＩＵ
课前预习教材 必备知识探究
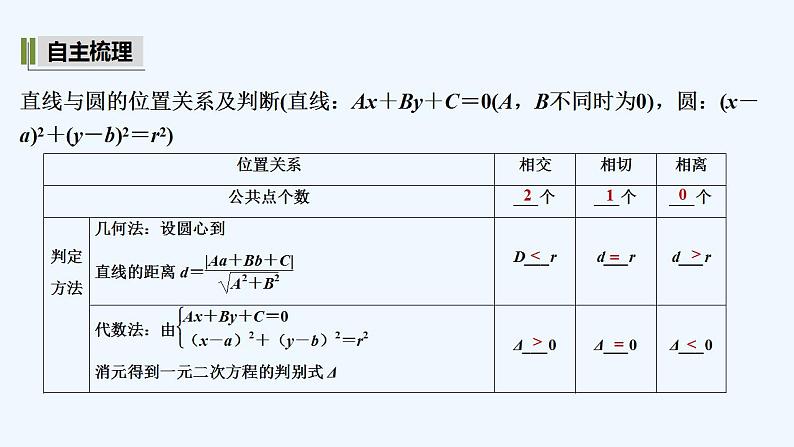
直线与圆的位置关系及判断(直线：Ax＋By＋C＝0(A，B不同时为0)，圆：(x－a)2＋(y－b)2＝r2)
1.思考辨析，判断正误(1)若直线与圆有公共点，则直线与圆相交.( )提示　直线与圆有公共点，则直线与圆相交或相切.(2)直线l：x＝0与圆x2＋y2＝1的位置关系是相交且过圆心.( )(3)若直线x－y＋a＝0与圆x2＋y2＝a(a>0)相切，则a等于4.( )
(4)直线x＋2y－1＝0与圆2x2＋2y2－4x－2y＋1＝0的位置关系是相交.( )
2.已知直线x＝a(a>0)和圆(x－1)2＋y2＝4相切，那么a的值是(　　)A.5 B.4 C.3 D.2解析　由题意知圆心(1，0)到直线x＝a的距离为2，即|a－1|＝2(a>0)，解之得a＝3.
3.直线y＝x＋1与圆x2＋y2＝1的位置关系是(　　)A.相切B.相交但直线不过圆心C.直线过圆心D.相离
又∵直线y＝x＋1不过圆心(0，0)，∴选B.
解析　由题意点P在圆上且P为切点.
ＫＥＴＡＮＧＹＡＮＸＩＴＩＸＩＮＧ ＧＵＡＮＪＩＡＮＮＥＮＧＬＩＴＩＳＨＥＮＧ
课堂研析题型 关键能力提升
例1 已知圆的方程是x2＋y2＝2，直线y＝x＋b，当b为何值时，圆与直线相交、相切、相离？
有两组不同实数解；有一组实数解；无实数解的问题.②代入①，整理得2x2＋2bx＋b2－2＝0，　③方程③的根的判别式Δ＝(2b)2－4×2(b2－2)＝－4(b＋2)(b－2).当－20，方程组有两组不同实数解，因此直线与圆有两个公共点，直线与圆相交；
当b＝2或b＝－2时，Δ＝0，方程组有一组实数解，因此直线与圆只有一个公共点，直线与圆相切；当b<－2或b>2时，Δ<0，方程组没有实数解，因此直线与圆没有公共点，直线与圆相离.综上，当－22或b<－2时，直线与圆相离.
∴b>2或b<－2.综上当－22或b<－2时，直线与圆相离.
训练1 (1)已知圆C：x2＋y2－4x＝0，l是过点P(3，0)的直线，则(　　)A.l与C相交B.l与C相切C.l与C相离 D.以上三个选项均有可能
解析　将点P(3，0)代入圆的方程，得32＋02－4×3＝9－12＝－3<0，∴点P(3，0)在圆内.∴过点P的直线l必与圆C相交.
(2)若直线x－y＝0与圆(x－1)2＋(y＋1)2＝m相离，则实数m的取值范围是(　　)A.(0，2] B.(1，2]C.(0，2) D.(1，2)
∴m<2，∵m>0，∴0例2 (1)过点M(2，4)向圆(x－1)2＋(y＋3)2＝1引切线，则其切线的方程为____________________________.
24x－7y－20＝0或x＝2
解析　由于(2－1)2＋(4＋3)2＝50>1，故点M在圆外.当切线斜率存在时，设切线方程是y－4＝k(x－2)，即kx－y＋4－2k＝0，
所以切线方程为24x－7y－20＝0.又当切线斜率不存在时，直线x＝2与圆相切.综上所述，所求切线方程为24x－7y－20＝0或x＝2.
(2)若圆C：x2＋y2＋2x－4y＋3＝0关于直线2ax＋by＋6＝0对称，则由点(a，b)向圆作的切线长的最小值是(　　)A.2 B.3 C.4 D.6
训练3 (1)过点(3，1)作圆(x－2)2＋(y－2)2＝4的弦，其中最短弦的长为________.
解析　设点A(3，1)，易知圆心C(2，2)，半径r＝2.当弦过点A(3，1)且与CA垂直时为最短弦，
(x－2)2＋(y＋1)2＝4
∴r2＝2＋2＝4，得r＝2.∴圆的方程为(x－2)2＋(y＋1)2＝4.
1.研究圆的切线问题时要注意切线的斜率是否存在.过一点求圆的切线方程时，要考虑该点是否在圆上.当点在圆上时，切线只有一条；当点在圆外时，切线有两条.2.弦长公式的两种表达(1)一般地，在解决圆和直线相交问题时，应首先考虑圆心到直线的距离、弦长的一半、圆的半径构成的直角三角形.(2)还可以联立方程组，消去y(或x)，得到一个一元二次方程，利用方程根与系数的关系表达出弦长.
ＫＥＨＯＵＦＥＮＣＥＮＧＪＩＮＧＬＩＡＮＨＥＸＩＮＳＵＹＡＮＧＤＡＣＨＥＮＧ
课后分层精练 核心素养达成
1.已知点M(a，b)在圆O：x2＋y2＝1外，则直线ax＋by＝1与圆O的位置关系是(　　)A.相切 B.相交C.相离 D.不确定解析　∵点M(a，b)在圆x2＋y2＝1外，∴a2＋b2＞1.
2.若a2＋b2＝2c2(c≠0)，则直线ax＋by＋c＝0被圆x2＋y2＝1所截得的弦长为(　　)
3.直线l与圆x2＋y2＋2x－4y＋a＝0(a<5)相交于A，B两点，若弦AB的中点为C(－2，3)，则直线l的方程为(　　)A.x－y＋5＝0 B.x＋y－1＝0C.x－y－5＝0 D.x＋y－3＝0
解析　由圆的一般方程，可得圆心为M(－1，2).由圆的性质易知，点M(－1，2)与C(－2，3)的连线与弦AB垂直，故有kAB·kMC＝－1，
故直线AB的方程为y－3＝x＋2，整理得x－y＋5＝0.
4.已知圆C与直线x－y＝0及x－y－4＝0都相切，且圆心C在直线x＋y＝0上，则圆C的方程为(　　)A.(x＋1)2＋(y－1)2＝2B.(x－1)2＋(y＋1)2＝2C.(x－1)2＋(y－1)2＝2D.(x＋1)2＋(y＋1)2＝2
解析　由x－y＝0与x－y－4＝0都与圆相切，且直线x－y＝0与x－y－4＝0平行，知圆C的圆心C在直线x－y－2＝0上.
故圆C的方程为(x－1)2＋(y＋1)2＝2.
5.(多选)平行于直线2x＋y＋1＝0且与圆x2＋y2＝5相切的直线的方程可以是(　　)
解析　依题意可设所求切线方程为2x＋y＋c＝0(c≠1)，
故所求切线方程为2x＋y＋5＝0或2x＋y－5＝0.
6.若直线y＝kx与圆x2＋y2－6x＋8＝0相切，且切点在第四象限，则k＝________.
7.直线y＝x＋2被圆M：x2＋y2－4x－4y－1＝0所截得的弦长为________.
8.由直线y＝x＋1上的一点A向圆C：x2－6x＋y2＋8＝0引切线，则切线长的最小值为________.
解析　由x2－6x＋y2＋8＝0，得(x－3)2＋y2＝1，故C(3，0)，r＝1.当AC与直线y＝x＋1垂直时，切线长取得最小值.
9.已知曲线C：x2＋y2＋2x＋4y＋m＝0.(1)当m为何值时，曲线C表示圆？
解　由C：x2＋y2＋2x＋4y＋m＝0，得(x＋1)2＋(y＋2)2＝5－m，由5－m>0时，得m<5，∴当m<5时，曲线C表示圆.
(2)若直线l：y＝x－m与圆C相切，求m的值.
∵直线l：y＝x－m与圆C相切，
解得：m＝±3，满足m<5.∴m＝±3.
10.已知圆C：(x－1)2＋(y－2)2＝25，直线l：(2m＋1)x＋(m＋1)y－7m－4＝0(m∈R).(1)求证不论m取什么实数，直线l与圆恒交于两点；
证明　l的方程可化为(x＋y－4)＋m(2x＋y－7)＝0(m∈R)，
即l恒过定点A(3，1).
所以点A在圆C内，从而直线l与圆C恒交于两点.
(2)求直线被圆C截得的弦长最小时的l的方程.
又l过点A(3，1)，所以l的方程为2x－y－5＝0.
12.圆x2＋y2－4x＋6y－12＝0过点(－1，0)的最大弦长为________，最小弦长为________.
解析　圆的方程x2＋y2－4x＋6y－12＝0化为标准方程为(x－2)2＋(y＋3)2＝25.所以圆心为(2，－3)，半径长为5.因为(－1－2)2＋(0＋3)2＝18＜25，所以点(－1，0)在已知圆的内部，则最大弦长即为圆的直径，即最大值为10.
13.如图，已知以点A(－1，2)为圆心的圆与直线l1：x＋2y＋7＝0相切.过点B(－2，0)的动直线l与圆A交于M，N两点.
解　设圆A的半径为r.∵圆A与直线l：x＋2y＋7＝0相切，
∴圆A的方程为(x＋1)2＋(y－2)2＝20.
解　①当直线l与x轴垂直时，直线l的方程为x＝－2，
②当直线l与x轴不垂直时，设直线l的方程为y＝k(x＋2)，即kx－y＋2k＝0.取MN的中点Q，连接AQ，则AQ⊥MN.
∴直线l的方程为3x－4y＋6＝0.综上，直线l的方程为x＝－2或3x－4y＋6＝0.
14.已知圆x2＋y2＋2ax－2ay＋2a2－4a＝0(0(2)若直线l是圆心下方的切线，当a在(0，4]变化时，求m的取值范围.
∵点C在直线l的上方，∴a>－a＋m，即2a>m，