









数学选择性必修第一册5.1 导数的概念教课课件ppt
展开5.1 导数的概念
5.1.1 平均变化率
课标要求 1.通过实例,了解平均变化率的概念,并会求具体函数的平均变化率.2.了解平均变化率概念的形成过程,会在具体的情境中,说明平均变化率的实际意义.
素养要求 1.通过具体的平均变化率问题,培养学生的数学建模素养.2.借助平均变化率的求解,提升学生的数学运算素养.
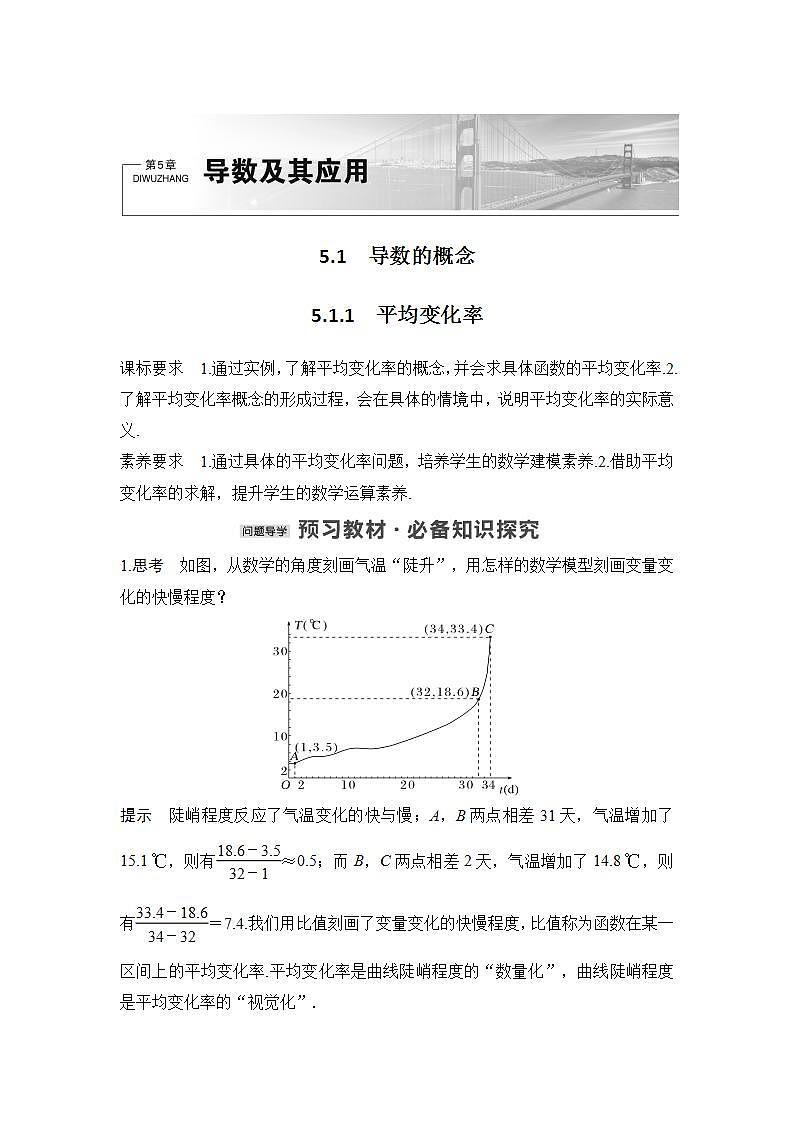
1.思考 如图,从数学的角度刻画气温“陡升”,用怎样的数学模型刻画变量变化的快慢程度?
提示 陡峭程度反应了气温变化的快与慢;A,B两点相差31天,气温增加了15.1 ℃,则有≈0.5;而B,C两点相差2天,气温增加了14.8 ℃,则有=7.4.我们用比值刻画了变量变化的快慢程度,比值称为函数在某一区间上的平均变化率.平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“视觉化”.
2.填空 (1)函数的平均变化率
一般地,函数f(x)在区间[x1,x2]上的平均变化率为.
(2)平均变化率的意义
平均变化率的几何意义是经过曲线y=f(x)上两点P(x1,y1),Q(x2,y2)的直线PQ的斜率.因此平均变化率是曲线陡峭程度的“数量化”,或者说,曲线陡峭程度是平均变化率的“视觉化”.
温馨提醒 x2-x1,f(x2)-f(x1)可正可负,f(x2)-f(x1)也可以为零,但x2-x1不能为零.平均变化率可正、可负、可为零.
3.做一做 已知函数f(x)=x2+1,则当x由2变到2.1时,函数值的改变量为( )
A.0.40 B.0.41
C.0.43 D.0.44
答案 B
解析 f(2.1)-f(2)=2.12+1-(22+1)=0.41.故选B.
题型一 求函数的平均变化率
例1 (1)函数f(x)=在[2,6]上的平均变化率为________.
答案 -
解析 ==-.
(2)已知函数f(x)=x+,分别计算f(x)在自变量x从1变到2和从3变到5时的平均变化率,并判断在哪个区间上函数值变化得较快.
解 自变量x从1变到2时,函数f(x)的平均变化率为==;
自变量x从3变到5时,函数f(x)的平均变化率为=
=.
因为<,所以函数f(x)=x+在自变量x从3变到5时函数值变化得较快.
思维升华 求函数平均变化率的三个步骤
第一步,求自变量的增量x2-x1;
第二步,求函数值的增量f(x2)-f(x1);
第三步,求平均变化率.
训练1 某森林公园在过去的10年里,森林占地面积变化如图所示,试分别计算前5年与后5年森林面积的平均变化率.
解 前5年森林面积的平均变化率为=0.8(公顷/年).
后5年森林面积的平均变化率为=1.6(公顷/年).
题型二 实际问题中的平均变化率
例2 在高台跳水运动中,运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10.
(1)求运动员在第一个0.5 s内高度h的平均变化率;
(2)求高度h在1≤t≤2这段时间内的平均变化率.
解 (1)运动员在第一个0.5 s内高度h的平均变化率为=4.05(m/s).
(2)在1≤t≤2这段时间内,高度h的平均变化率为=-8.2 (m/s).
思维升华 实际问题中的平均变化率与函数在某一区间上的平均变化率类似,首先求f(x2)-f(x1),再求比值.当函数解析式没有给定时,先根据实际问题求出函数解析式,再重复上述步骤即可.
训练2 一质点作直线运动,其位移s与时间t的关系为s(t)=t2+1,该质点在2到2+Δt(Δt>0)之间的平均速度不大于5,则Δt的取值范围是________.
答案 (0,1]
解析 质点在2到2+Δt之间的平均速度为v===4+Δt,又v≤5,则4+Δt≤5,所以Δt≤1,又Δt>0,所以Δt的取值范围是(0,1].
题型三 平均变化率的应用
例3 为了检测甲、乙两辆车的刹车性能,分别对两辆车进行了测试,甲车从25 m/s到0 m/s花了5 s,乙车从18 m/s到0 m/s花了4 s,试比较两辆车的刹车性能.
解 甲车速度的平均变化率为=-5(m/s2),乙车速度的平均变化率为=-4.5(m/s2),
平均变化率为负值说明速度在减少,因为刹车后,甲车的速度变化相对较快,所以甲车的刹车性能较好.
思维升华 平均变化率的应用主要有:求某一时间段内的平均速度,物体受热膨胀率,高度(重量)的平均变化率等等.解决这些问题的关键在于找准自变量和因变量.
训练3 已知气球的体积V(单位:L)与半径r(单位:dm)之间的函数关系是V(r)=πr3.
(1)求半径r关于体积V的函数r(V);
(2)比较体积V从0 L增加到1 L和从1 L增加到2 L半径r的平均变化率;哪段半径变化较快(精确到0.01)?此结论可说明什么意义?
解 (1)∵V=πr3,
∴r3=,r=,
即r(V)=.
(2)函数r(V)在区间[0,1]上的平均变化率约为=≈0.62(dm/L),
函数r(V)在区间[1,2]上的平均变化率约为=-
≈0.16(dm/L).
显然体积V从0 L增加到1 L时,半径变化快,这说明气球刚开始膨胀的比较快,随着体积的增大,半径增加的越来越慢.
[课堂小结]
1.牢记1个知识点
平均变化率对函数而言,即是函数值的改变量与自变量的改变量的比值,即平均变化率为.
2.明确平均变化率的意义
平均变化率的绝对值越大,表示函数值变化得越快,绝对值越小,表示函数值变化得越慢.平均变化率的正负只表示变化的方向.
一、基础达标
1.已知函数y=2+,当x由1变到2时,函数值的改变量等于( )
A. B.-
C.1 D.-1
答案 B
解析 函数值的改变量为-(2+1)=-.
2.已知函数f(x)=x2+2,则该函数在区间[1,3]上的平均变化率为( )
A.4 B.3
C.2 D.1
答案 A
解析 ∵f(3)=11,f(1)=3,
∴该函数在区间[1,3]上的平均变化率为==4.
3.一物体的运动方程是s=3+2t,则在[2,2.1]这段时间内的平均变化率为( )
A.0.4 B.2
C.0.3 D.0.2
答案 B
解析 在[2,2.1]这段时间内的平均变化率为=2.
4.某物体的运动方程为s=5-2t2,则该物体在时间[1,1+d]上的平均速度为( )
A.2d+4 B.-2d+4
C.2d-4 D.-2d-4
答案 D
解析 平均速度为=-2d-4.故选D.
5.函数y=x2在区间[x0,x0+Δx]上的平均变化率为k1,在区间[x0-Δx,x0]上的平均变化率为k2,则( )
A.k1>k2 B.k1<k2
C.k1=k2 D.不确定
答案 A
解析 因为k1==2x0+Δx,k2==2x0-Δx,
又由题意知Δx>0,所以k1>k2.
6.函数f(x)=log2x在区间[2,4]上的平均变化率是________.
答案
解析 函数的平均变化率是
==.
7.如图所示为物体甲、乙在时间0到t1范围内路程的变化情况,则在0到t0范围内甲的平均速度________乙的平均速度,在t0到t1范围内甲的平均速度________乙的平均速度(填“等于”“大于”或“小于”).
答案 等于 大于
解析 由图可知,在[0,t0]上,甲的平均速度与乙的平均速度相同;在[t0,t1]上,甲的平均速度大于乙的平均速度.
8.若函数y=x3+2在区间[1,a]上的平均变化率为21,则a=________.
答案 4
解析 由==a2+a+1=21,
解得a=4或a=-5.
又∵a>1,∴a=4.
9.求函数f(x)=x2++4在区间[1,2]上的平均变化率.
解 f(x)=x2++4在区间[1,2]上的平均变化率为=.
10.求函数y=sin x在0到之间和到之间的平均变化率,并比较它们的大小.
解 在0到之间的平均变化率为=;
在到之间的平均变化率为=.
∵2-<1,∴>,
∴函数y=sin x在0到之间的平均变化率较大.
二、能力提升
11.如图是函数y=f(x)的图象,函数f(x)在区间[-1,1],[0,2]上的平均变化率分别为m1,m2,则m1,m2的大小关系是( )
A.m1>m2 B.m1<m2
C.m1=m2 D.无法确定
答案 B
解析 函数f(x)在区间[-1,1]上的平均变化率为m1===.
由函数f(x)的图象知,f(x)=
所以函数f(x)在区间[0,2]上的平均变化率为m2===.
所以m1<m2.
12.函数f(x)的图象如图,则函数f(x)在下列区间上平均变化率最大的是( )
A.[1,2] B.[2,3]
C.[3,4] D.[4,7]
答案 C
解析 函数f(x)在区间上[x1,x2]的平均变化率为,
由函数图象可得,在区间[4,7]上,<0,即函数f(x)在区间[4,7]上的平均变化率小于0;
在区间[1,2],[2,3],[3,4]上,>0,由图象可知函数在区间[3,4]上的平均变化率最大.
所以函数f(x)在区间[3,4]上的平均变化率最大.
13.已知函数f(x)=2x2+1.
(1)求函数f(x)在[2,2.01]上的平均变化率;
(2)求函数f(x)在[x0,x0+Δx]上的平均变化率.
解 (1)由f(x)=2x2+1,
得f(2.01)-f(2)=0.080 2,
又2.01-2=0.01,
∴==8.02.
(2)∵f(x0+Δx)-f(x0)=2(x0+Δx)2+1-2x-1=2Δx(2x0+Δx),
∴==4x0+2Δx.
三、创新拓展
14.函数f(x)=x,g(x)=x2,h(x)=x3在[0,1]上的平均变化率分别记为m1,m2,m3,则下列结论正确的是( )
A.m1=m2=m3 B.m1>m2>m3
C.m2>m1>m3 D.m1<m2<m3
答案 A
解析 m1==f(1)-f(0)=1-0=1,
m2==g(1)-g(0)=12-0=1,
m3==h(1)-h(0)=13-0=1,故m1=m2=m3,故选A.
人教A版 (2019)选择性必修 第二册5.1 导数的概念及其意义精品ppt课件: 这是一份人教A版 (2019)选择性必修 第二册5.1 导数的概念及其意义精品ppt课件,文件包含511《变化率问题》课件pptx、511《变化率问题》教案docx等2份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
高中数学苏教版 (2019)必修 第一册7.1 角与弧度评课课件ppt: 这是一份高中数学苏教版 (2019)必修 第一册7.1 角与弧度评课课件ppt,文件包含711任意角pptx、711任意角doc等2份课件配套教学资源,其中PPT共57页, 欢迎下载使用。
高中数学苏教版 (2019)必修 第一册6.1 幂函数图片ppt课件: 这是一份高中数学苏教版 (2019)必修 第一册6.1 幂函数图片ppt课件,文件包含61幂函数pptx、61幂函数doc等2份课件配套教学资源,其中PPT共55页, 欢迎下载使用。














