高中数学北师大版 (2019)必修 第一册1 对数的概念评课ppt课件

这是一份高中数学北师大版 (2019)必修 第一册1 对数的概念评课ppt课件，文件包含§1对数的概念pptx、§1对数的概念doc等2份课件配套教学资源，其中PPT共46页， 欢迎下载使用。

1.理解对数的概念.2.知道自然对数和常用对数.3.通过阅读材料，了解对数的发现历史以及对简化运算的作用.
通过本节内容的学习，使学生理解对数的概念，会用对数的定义进行对数式与指数式的互化，会求简单的对数值，感受对数性质的应用，从而提高学生的逻辑推理及数学运算素养.
问题导学预习教材必备知识探究
互动合作研析题型关键能力提升
拓展延伸分层精练核心素养达成
WEN TI DAO XUE YU XI JIAO CAI BI BEI ZHI SHI TAN JIU
问题导学预习教材 必备知识探究
一、对数的概念1.思考　某种细胞分裂时，由1个分裂成2个，2个分裂成4个，…依次类推，那么1个这样的细胞分裂x次后，得到的细胞个数N是多少？上述问题中，如果已知细胞分裂后的个数N，能求出分裂次数x吗？提示　N＝2x；能，x＝lg2N.
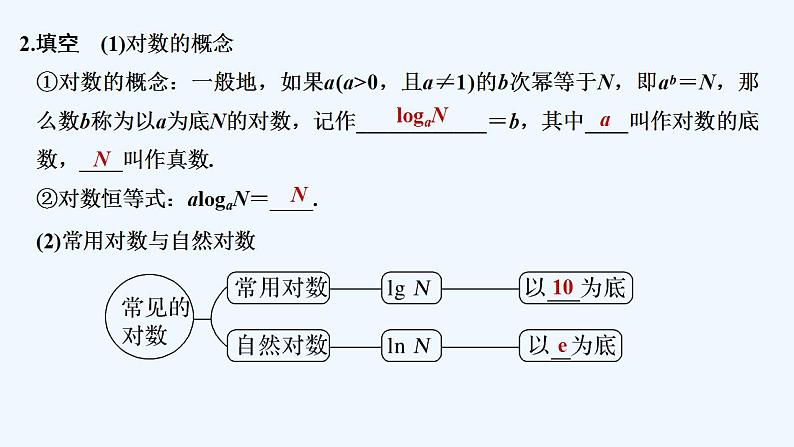
2.填空　(1)对数的概念①对数的概念：一般地，如果a(a>0，且a≠1)的b次幂等于N，即ab＝N，那么数b称为以a为底N的对数，记作____________＝b，其中____叫作对数的底数，____叫作真数.②对数恒等式：algaN＝____.
(2)常用对数与自然对数
温馨提醒　(1)在对ax＝N和x＝lgaN(a>0且a≠1)进行互化时，要分清字母在指数式和对数式中的位置.(2)对数与指数的关系：
3.做一做　(1)将2x＝7化成对数式可表示为(　　)A.lg72＝x B.lg27＝xC.lg2x＝7 D.lg7x＝3
(2)使对数lga(－2a＋1)有意义的a的取值范围为(　　)
二、对数的基本性质1.思考　是不是所有的实数都有对数？为什么？提示　零和负数没有对数.因为ax＝N(a＞0且a≠1)中无论x取什么值，N总大于0，故零和负数无对数.
2.思考　根据对数的定义以及对数与指数的关系，你能求出lga1及lgaa的值吗？提示　设lga1＝x，则ax＝1＝a0，故x＝0，即lga1＝0，同理lgaa＝1.
3.思考　根据对数的定义，你能推出对数恒等式algaN＝N吗？提示　因为ax＝N，x＝lgaN，所以algaN＝N.
4.填空　对数的基本性质(1)负数和零______对数.(2)lga1＝____ (a>0，且a≠1).(3)lgaa＝____ (a>0，且a≠1).
5.做一做　(1)思考辨析，判断正误①(－2)3＝－8可化为lg(－2)(－8)＝3.()提示　lgaN必须满足a>0且a≠1.②3lg3(－4)＝－4.()提示　algaN＝N，须a>0且a≠1，N>0.(2)计算lg2 0221＋lg2 0222 022＋eln 3＝________.解析　原式＝0＋1＋3＝4.
HU DONG HE ZUO YAN XI TI XING GUAN JIAN MENG LI TI SHENG
互动合作研析题型 关键能力提升
例1　(1)在对数式y＝lg(x－2)(4－x)中，实数x的取值范围是_______________.
(2，3)∪(3，4)
解　①由54＝625，得lg5625＝4；②由lg216＝4，得24＝16；③由10－2＝0.01，得lg 0.01＝－2；
(1)指数式化为对数式：将指数式的幂作为真数，指数作为对数，底数不变，写出对数式.(2)对数式化为指数式：将对数式的真数作为幂，对数作为指数，底数不变，写出指数式.
训练1　将下列指数式、对数式互化：
解　(1)因为43＝64，所以lg464＝3；(2)因为ln a＝b，所以eb＝a；
例2　(1)求下列各式的值.
题型二　利用指数式与对数式的互化求变量的值
①lg981＝________.②lg0.41＝________.③ln e2＝________.
解析　①设lg981＝x，所以9x＝81＝92，故x＝2，即lg981＝2；②设lg0.41＝x，所以0.4x＝1＝0.40，故x＝0，即lg0.41＝0；③设ln e2＝x，所以ex＝e2，故x＝2，即ln e2＝2.
③由lg 100＝x，得10x＝100＝102，即x＝2；④由－ln e2＝x，得ln e2＝－x，所以e－x＝e2，－x＝2，x＝－2.
对数式中求值的基本思想和方法(1)基本思想在一定条件下求对数的值，或求对数式中参数的值，要注意利用方程思想求解.(2)基本方法①将对数式化为指数式，构建方程转化为指数问题.②利用幂的运算性质和指数的性质计算.
训练2　利用指数式、对数式的互化求下列各式中的x值.
(2)由lgx25＝2，得x2＝25.∵x＞0，且x≠1，∴x＝5；(3)由lg5x2＝2，得x2＝52，∴x＝±5.
题型三　利用对数的性质及对数恒等式求值
(3)原式＝(algab)lgbc＝blgbc＝c；(4)由lg3(lg4(lg5x))＝0，可知lg4(lg5x)＝1，可知lg5x＝4，∴x＝54＝625.
迁移1　本例(4)中若将“lg3(lg4(lg5x))＝0”改为“lg3(lg4(lg5x))＝1”，又如何求解x呢？解　由lg3(lg4(lg5x))＝1，可知lg4(lg5x)＝3.可知lg5x＝43＝64，∴x＝564.
迁移2　本例(4)中若将“lg3(lg4(lg5x))＝0”改为“3lg3(lg4(lg5x))＝1”，又如何求解x呢？解　由3lg3(lg4(lg5x))＝1，可知lg3(lg4(lg5x))＝0，可知lg4(lg5x)＝1，可知lg5x＝4，∴x＝54＝625.
对于不能直接应用对数恒等式的情况按以下步骤求解.
训练3　(1)设3lg3(2x＋1)＝27，则x＝________.(2)若lgπ(lg3(ln x))＝0，则x＝________.
解析　(1)3lg3(2x＋1)＝2x＋1＝27，解得x＝13.(2)由lgπ(lg3(ln x))＝0可知lg3(ln x)＝1，所以ln x＝3，解得x＝e3.
1.牢记指、对数式互化ab＝N⇔b＝lgaN＝N(a>0且a≠1，N>0).2.掌握2个恒等式①lgaab＝b；②algaN＝N(a>0且a≠1，N＞0).3.熟记3条性质①lgaa＝1；②lga1＝0；③0与负数无对数，其中a>0且a≠1.4.辨清1个易错点易忽略对数的真数大于0.
TUO ZHAN YAN SHEN FEN CENG JING LIAN HE XING SU YANG DA CHENG
拓展延伸分层精练 核心素养达成
1.(多选)下列选项中，可以求对数的是(　　)A.0 B.－5 C.π D.x2＋1解析　根据对数的定义，得0和负数没有对数，所以选项A，B没有对数，π＞0，选项C有对数，又x2＋1≥1，所以选项D有对数.
2.lgab＝1成立的条件是(　　)A.a＝b B.a＝b且b>0C.a>0，a≠1 D.a>0，a＝b≠1解析　由lgab＝1得a>0，且a＝b≠1.
3.设a＝lg310，b＝lg37，则3a－b的值为(　　)
5.(多选)下列式子中正确的是(　　)
解析　∵lg 10＝1，∴lg(lg 10)＝lg 1＝0，A正确；∵ln e＝1，∴lg(ln e)＝lg 1＝0，B正确；若10＝lg x，则x＝1010，C不正确；
7.若lg3(a＋1)＝1，则lga2＋lg2(a－1)＝________.
解析　由lg3(a＋1)＝1得a＋1＝3，即a＝2，所以lga2＋lg2(a－1)＝lg22＋lg21＝1＋0＝1.
8.十六、十七世纪之交，随着天文、航海、工程、贸易以及军事的发展，改进数字计算方法成了当务之急，数学家纳皮尔在研究天文学的过程中，为简化计算发明了对数，直到十八世纪才由瑞士数学家欧拉发现了指数与对数的互逆关系，即ab＝N⇔b＝lgaN，现在已知a＝lg48，b＝lg24，则4a＝________，a＋b＝________(用最简结果作答).
解析　∵a＝lg48，b＝lg24，则4a＝4lg48＝8，
由b＝lg24，∴2b＝4，即2b＝22，∴b＝2，
9.将下列指数式、对数式互化.
10.求下列各式中的x的值.
11.对于a>0且a≠1，下列说法正确的是(　　)①若M＝N，则lgaM＝lgaN；②若lgaM＝lgaN，则M＝N；③若lgaM2＝lgaN2，则M＝N；④若M＝N，则lgaM2＝lgaN2.A.①② B.②③④ C.② D.②③解析　①中若M，N小于或等于0时，lgaM＝lgaN不成立；②正确；③中M与N也可能互为相反数；④中当M＝N＝0时不正确.
解析　设2＋lg2a＝3＋lg3b＝lg6(a＋b)＝k，则a＝2k－2，b＝3k－3，a＋b＝6k，即4a＝2k，27b＝3k，所以108ab＝6k，∴108ab＝a＋b，
13.已知lg(2x2－1)(3x2＋2x－1)＝1，求x的值.