新高考数学二轮专题《立体几何》第20讲 立体几何综合问题（2份打包，解析版+原卷版）

第20讲 立体几何综合问题

一．解答题（共14小题）

1．如图，直线平面，直线平行四边形，四棱锥的顶点在平面上，，，，，，，，分别是与的中点．

（1）求证：平面；

（2）求二面角的余弦值．

【解答】【答案】

（1）连接，，底面为平行四边形，

是的中点，是的中点，

，

是的中点，是的中点，，，，

平面平面，平面，平面；

（2）由平面，平行四边形

平面底面，，，

四边形为矩形，且底面，，

过作，以，，所在直线分别为，，轴建立空间直角坐标系（如图）

由，知，

，，，

设平面的法向量，

则，取，，，即，

设平面的法向量，

则，取，，，即，

二面角的平面角的余弦值．

2．如图，四边形为菱形，，，是平面同一侧的两点，平面，平面，，．

证明：平面平面；

求二面角的余弦值．

【解答】证明：连接，设，连接，，，

在菱形中，不妨设，由，可得．

由平面，可知，，

又，，，

在中，可得，故．

在中，可得．

在直角梯形中，由，，可得，

，，，平面，

面，平面平面．

解：如图，以为坐标原点，分别以的方向为轴，轴正方向，为单位长度，建立空间直角坐标系，

由（Ⅰ）可得，0，，，0，，，0，，，，，

，，

设平面、平面的法向量分别为，

则，

可得面与面的法向量，

，即面面，所以二面角的余弦值为0

3．如图，四棱锥中，，，侧面为等边三角形．，．

（1）证明：平面

（2）求与平面所成角的正弦值．

【解答】（1）证明：取中点，连结，则四边形为矩形，．

连结，则

又，故

所以为直角，

所以，

由，，，得平面，所以．

因为，

所以平面分

（2）解：由平面知，平面平面．

作，垂足为，则平面，

作，垂足为，则．

连结，则

又，，

故平面，平面平面，

作，为垂足，则平面，

即到平面的距离为．

由于，所以平面，到平面的距离也为．

设与平面所成的角为，则分．

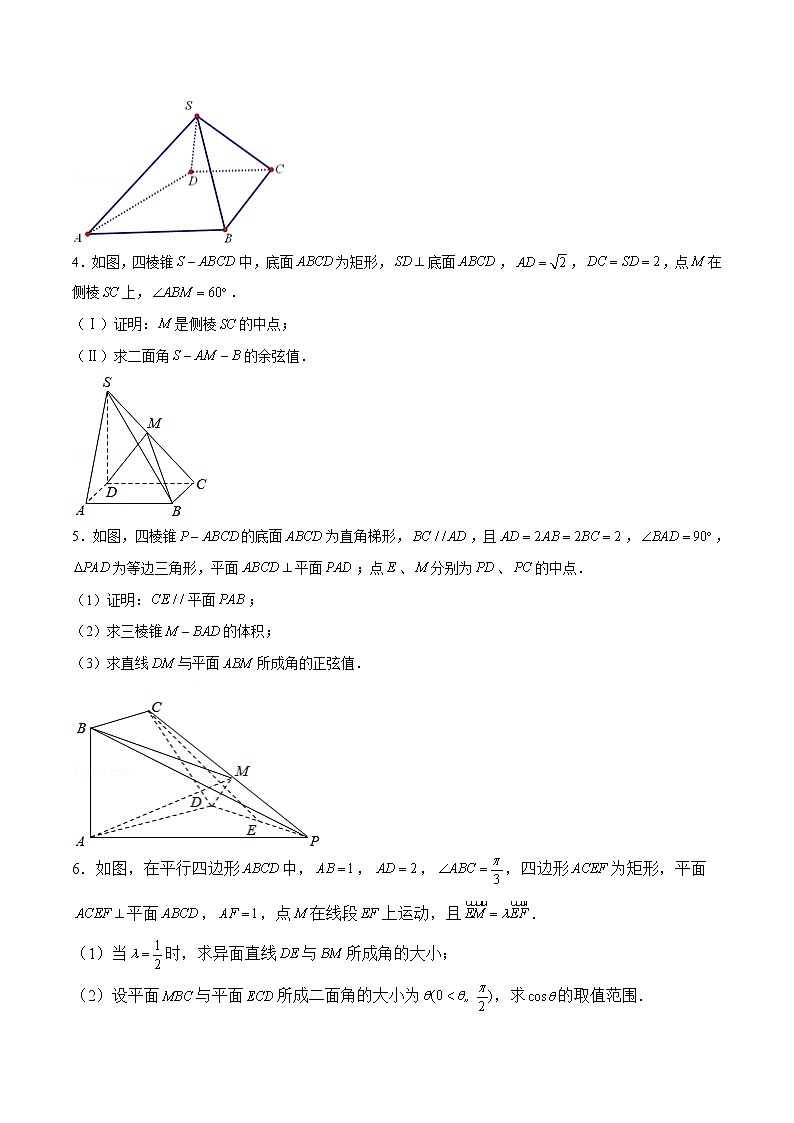
4．如图，四棱锥中，底面为矩形，底面，，，点在侧棱上，．

（Ⅰ）证明：是侧棱的中点；

（Ⅱ）求二面角的余弦值．

【解答】（Ⅰ）证明：作交于点，则，平面，

连接，则四边形为直角梯形，

作，垂足为，则为矩形，

设，则，，

，，

由，得，

解得，即，

从而，

为侧棱的中点．

（Ⅱ）解：，

又，，为等边三角形．

又由（Ⅰ）知为中点，，，，

，，

取中点，连结，取中点，连结，

则，，

由此知为二面角的平面角，

连结，在中，

，，，

．

二面角的余弦值为．

5．如图，四棱锥的底面为直角梯形，，且，，为等边三角形，平面平面；点、分别为、的中点．

（1）证明：平面；

（2）求三棱锥的体积；

（3）求直线与平面所成角的正弦值．

【解答】解：（1）证明：设的中点为，连结，，

为中点，为的中位线，

，且，

在梯形中，，且，

，且，四边形是平行四边形，，

平面，平面，平面．

（2）解：四棱锥的底面为直角梯形，，且，，

，

为等边三角形，平面平面，点是的中点．

设的中点为，则，，

到平面的距离，

三棱锥的体积．

（3）平面平面，交线为，平面，

平面，

又，，，

，，，两两垂直，

以为原点，，，，所在直线分别为，，轴，建立空间直角坐标系，

则，0，，，0，，，，，，0，，

，0，，，，，

设平面的法向量，，，

则，取，得，，，，

，

直线与平面所成角的正弦值为．

6．如图，在平行四边形中，，，，四边形为矩形，平面平面，，点在线段上运动，且．

（1）当时，求异面直线与所成角的大小；

（2）设平面与平面所成二面角的大小为，求的取值范围．

【解答】解：（1）在中，，，，

则，

，，

四边形为菱形，，

平面平面，平面平面，

平面，平面，

以为原点，为轴，为轴，为轴，建立空间直角坐标系，

则，0，，，0，，，，，，，，，0，，

当时，，，，，

，，，，0，，

，，

异面直线与所成角的大小为．

（2）平面的一个法向量，1，，

设，，，

由，，，，，

得，，，

，，，，，，

设平面的法向量，，，

则，取，得，

，，

，，．

7．如图，在四棱锥中，侧面底面，底面为直角梯形，其中，，，，，，点在棱上且，点为棱的中点．

在棱上且，点位棱的中点．

（1）证明：平面平面；

（2）求二面角的余弦值的大小．

【解答】证明：（1）在中，由，得，

同理在中，由，得，

所以，即（亦可通过勾股定理来证明）

在中，

在，

所以，即

解：（2）由（1）知，，两两垂直，

故以为坐标原点，以射线，，分别为轴，轴，轴的正半轴建立如图所示的空间直角坐标系，

得，，，0，，，，，

，，，

设平面的法向量为

则：

不妨设，则

设平面的法向量为

则，

不妨设，则

记二面角为（应为钝角）

故二面角的余弦值为．

8．如图所示，该几何体是由一个直三棱柱和一个正四棱锥组合而成，，．

（Ⅰ）证明：平面平面；

（Ⅱ）求正四棱锥的高，使得二面角的余弦值是．

【解答】证明：（Ⅰ）几何体是由一个直三棱柱和一个正四棱锥组合而成，

，，

又，

平面，

又平面，

平面平面．

解：（Ⅱ）以 为原点，、、的正方向为，，轴，建立空间直角坐标系

设正四棱棱的高为，，

则，0，，，2，，，0，，，，

设平面的一个法向量，，，

，2，，，0，，

则，取，得，，，

设平面的一个法向量，，，

则，取，则，1，，

二面角的余弦值，

，

解得．

9．如图，在四棱锥中，四边形为梯形，，且，是边长为2的正三角形，顶点在上的射影为点，且，，．

（1）证明：平面平面；

（2）求二面角的余弦值．

【解答】证明：（1）由顶点在上投影为点，可知，．

取的中点为，连结，．

在中，，，所以．

在中，，，所以．

所以，，即．

，，

面．

又面，所以面面．

解：（2）由（Ⅰ）知，，，且

所以  面，且面．以所在直线为轴，所在直线为轴，

过点作平面的垂线为轴，建立空间直角坐标系，如图所示：

，，，，

，，，，，

设平面，的法向量分别为，，

则，即，取，得，，，

，即，取，得，

设二面角的平面角为．

则．

所以二面角的余弦值为．

10．如图，在斜三棱柱中，侧面与侧面都是菱形，，．

求证：；

若，求平面和平面所成锐二面角的余弦值．

【解答】证明：取中点为，连结，，，，

．

解：由及知，，又

，以，，分别为轴、轴、轴

建立空间直角坐标系，

则，，1，，，，，，

，，，，

设平面的法向量为，，，

平面的法向量为，，，

则，

取，，，，，

设平面与平面所成锐二面角为，

则．

平面和平面所成锐二面角的余弦值为．

11．在如图所示的空间几何体中，平面平面，与是边长为2的等边三角形，，和平面所成的角为，且点在平面上的射影落在的平分线上．

（1）求证：平面；

（2）求二面角．

【解答】证明：（1）由题意知，，都是边长为2的等边三角形

取中点，连接，，

则，，（2分）

又平面平面，

平面，作平面，

那么，根据题意，点落在上，

和平面所成的角为，

，

，，（4分）

四边形是平行四边形，

，

不包含于平面，平面，

平面（6分）

（2）以，，为轴，轴，轴建立如图所示的空间直角坐标系，

，，，，0，，，，，

，，，，，，

平面的一个法向量为，0，，

设平面的一个法向量为，，，

则，取，得，，，（9分）

，

又由图知，所求二面角的平面角是锐角，

二面角的余弦值为．（12分）

12．如图，在四面体中，已知，，

（1）求证：；

（2）若平面平面，且，求二面角的余弦值．

【解答】（1）证明：，，．

，

．

取的中点，连结，，则，．

又，

平面，平面，

平面，

．

（2）解：过作于点．则平面，

又平面平面，平面平面，

平面．

过做于点，连接．

平面，，又，

平面，．

为二面角的平面角．

连接．，．

，，

，．，．

，．

，

，二面角的余弦值为．

13．三棱柱的底面是等边三角形，的中点为，底面，与底面所成的角为，点在棱上，且，．

（1）求证：平面；

（2）求二面角的平面角的余弦值．

【解答】（1）证明：连接，底面，，底面，，，且与底面所成的角为，即．

在等边三角形中，易求得．

在中，由余弦定理，得，

，即．

又，．，，，

又，，平面，

又平面，，

又，平面．

（2）如下图所示，以为原点，分别以，，所在的直线为，，轴建立空间直角坐标系，

则

故

由（1）可知，可得点的坐标为，平面的一个法向量是．

设平面的法向量，，，由得，令，则，，

则，，

易知所求的二面角为钝二面角，二面角的平面角的余弦角值是．

14．如图，将矩形沿折成二面角，其中为的中点，已知，．，为的中点．

（1）求证：平面；

（2）求与平面所成角的正弦值．

【解答】证明：（1）取的中点，连结，，则，，

所以四边形是平行四边形，因此，（4分）

又平面，所以平面．（6分）

解：（2）取的中点，中点，连结，，，

由，所以，又，

所以平面，所以，

又，所以平面，所以平面平面，（8分）

又，所以平面，（9分）

所以，又，所以平面，（10分）

所以是与平面所成角，（12分）

又，，所以，（14分）

所以与平面所成角的正弦值．（15分）

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/4/3 11:04:25；用户：程长月；邮箱：hngsgz031@xyh.com；学号：25355879