新高考数学二轮专题《立体几何》第9讲 立体几何截面和交线问题（2份打包，解析版+原卷版）

第9讲 立体几何截面和交线问题

一．选择题（共13小题）

1．在棱长为2的正方体中，，分别为，的中点，则过，，三点的平面截该正方体，所得截面的周长为　　

A． B． C． D．

2．已知圆，过点的直线中被圆截得的最短弦长为，类比上述方法：设球是棱长为4的正方体的外接球，过该正方体的棱的中点作球的截面，则最小截面的面积为　　

A． B． C． D．

3．已知正方体的棱长为2，为的中点，若平面，且平面，则平面截正方体所得截面的周长为　　

A． B． C． D．

4．正方体棱长为4，，，分别是棱，，的中点，则过，，三点的平面截正方体所得截面的面积为　　

A． B． C． D．

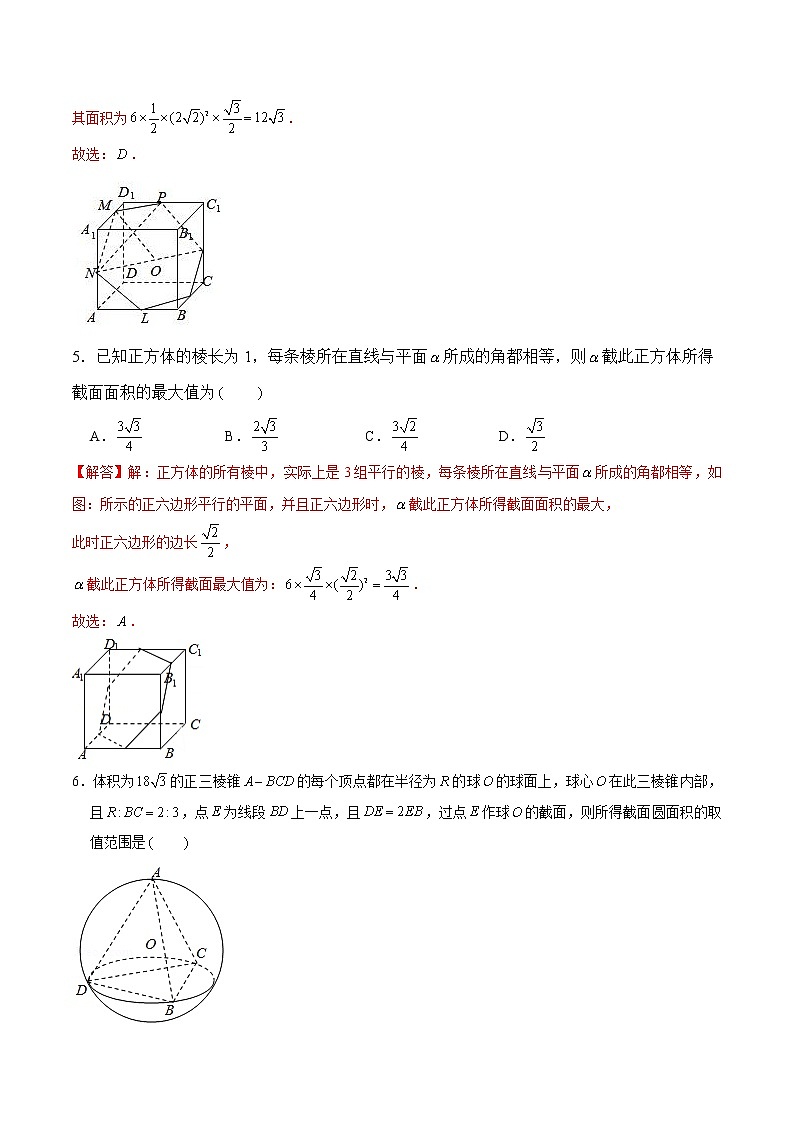
5．已知正方体的棱长为1，每条棱所在直线与平面所成的角都相等，则截此正方体所得截面面积的最大值为　　

A． B． C． D．

6．体积为的正三棱锥的每个顶点都在半径为的球的球面上，球心在此三棱锥内部，且，点为线段上一点，且，过点作球的截面，则所得截面圆面积的取值范围是　　

A．， B．， C．， D．，

7．圆锥的母线长为2，其侧面展开图的中心角为弧度，过圆锥顶点的截面中，面积的最大值为2；则的取值范围是　　

A． B． C． D．

8．如图，已知四面体为正四面体，，，分别是，中点．若用一个与直线垂直，且与四面体的每一个面都相交的平面去截该四面体，由此得到一个多边形截面，则该多边形截面面积最大值为　　

A． B． C． D．1

9．设四棱锥的底面不是平行四边形，用平面去截此四棱锥，使得截面四边形是平行四边形，则这样的平面　　

A．不存在 B．只有1个 C．恰有4个 D．有无数多个

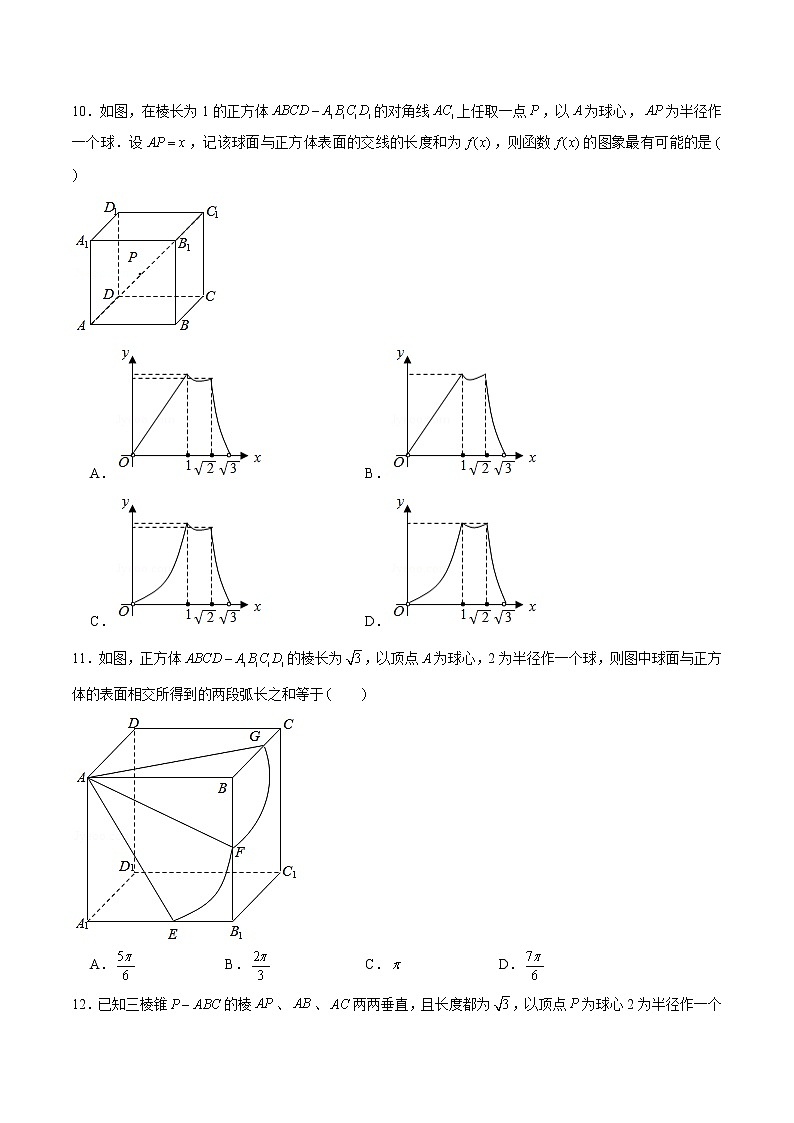
10．如图，在棱长为1的正方体的对角线上任取一点，以为球心，为半径作一个球．设，记该球面与正方体表面的交线的长度和为，则函数的图象最有可能的是　　

A． B． 

C． D．

11．如图，正方体的棱长为，以顶点为球心，2为半径作一个球，则图中球面与正方体的表面相交所得到的两段弧长之和等于　　

A． B． C． D．

12．已知三棱锥的棱、、两两垂直，且长度都为，以顶点为球心2为半径作一个球，则球面与三棱锥的表面相交所得到的四段弧长之和等于　　

A． B． C． D．

13．已知底面为正方形的四棱锥，各侧棱长都为，底面面积为16，以为球心，以2为半径作一个球，则这个球与四棱锥相交部分的体积是　　

A． B． C． D．

二．多选题（共2小题）

14．如图，在正方体中，，，，分别是所在棱的中点，则下列结论正确的是　　

A．点，到平面的距离相等 

B．与为异面直线 

C． 

D．平面截该正方体的截面为正六边形

15．如图，棱长为2的正方体的内切球为球，、分别是棱和棱的中点，在棱上移动，则下列结论成立的有　　

A．存在点，使垂直于平面 

B．对于任意点，平面 

C．直线的被球截得的弦长为 

D．过直线的平面截球所得的所有圆中，半径最小的圆的面积为

三．填空题（共17小题）

16．正方体的棱长为4，，分别是和的中点，经过点，，的平面把正方体截成两部分，则截面的周长为　　．

17．如图正方体的棱长为2，为的中点，为线段的中点，过点，，的平面截该正方体所得的截面的周长为　 　．

18．已知正方体的棱长为2，为的中点，若平面，且平面，则平面截正方体所得截面的周长为　　．

19．已知圆柱的上、下底面的中心分别为，，过直线的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为　　．

20．正方体棱长为4，，，分别是棱，，的中点，则过，，三点的平面截正方体所得截面的面积为　 　．

21．已知棱长为2的正方体，球与该正方体的各个面相切，则平面截此球所得的截面的面积为　 　．

22．球为正方体的内切球，，，分别为棱，的中点，则直线被球截得的线段长为　 　．

23．如图，动点在正方体的对角线上，过点作垂直于平面的直线，与正方体表面相交于，两点，设，，则函数的图象大致是　　．（在横线上填上正确的序号，多选少选都不得分）

24．如图，正方体的棱长为，以顶点为球心，2为半径作一个球，则图中球面与正方体的表面相交所得到的两段弧长之和等于　 　．

25．已知正方体的棱长为1，以顶点为球心，为半径作一个球，则球面与正方体的表面相交所得到的曲线的长等于　　．

26．已知正三棱锥侧棱长为1，且、、两两垂直，以顶点为球心，为半径作一个球，则球面与正三棱锥的表面相交得到一条封闭的曲线，则这条封闭曲线的长度为　　．

27．以棱长为2的正方体中心点为球心，以为半径的球面与正方体的表面相交得到若干个圆（或圆弧）的总长度的取值范围是　 　．

28．正方体棱长为2，以其体对角线的交点为球心，为半径的球与正方体表面的交线长为　　．

29．已知正方体的棱长为4，以该正方体的一个顶点为球心，以为球的半径作球面，则该球面被正方体表面所截得的所有弧长的和为　　．

30．如图，正方体的棱长为1，为的中点，为线段上的动点，过点，，的平面截该正方体所得截面记为，则下列命题正确的是　　（写出所有正确命题的编号）

①当时，为四边形

②当时，为等腰梯形

③当时，与的交点满足

④当时，为四边形

⑤当时，的面积为

31．如图，正方体的棱长为1，为的中点，为线段上的动点，过点，，的平面截该正方体所得的截面记为，若，则的面积取值范围是　　．

32．如图，正方体的棱长为1，为的中点，为线段上的动点，过点，，的平面截正方体所得的截面为，当时，的面积为　　．

四．解答题（共5小题）

33．如图，在正三棱锥中，，，平行于、的截面分别交、、、于点、、、．

（1）判定四边形的形状，并说明理由．

（2）设是棱上的点，当为何值时，平面平面，请给出证明．

34．如图所示，在正方体中，点在棱上，且，点、、分别是棱、、的中点，为线段上一点，．

（Ⅰ）若平面交平面于直线，求证：；

（Ⅱ）若直线平面．

求三棱锥的表面积；

试作出平面与正方体各个面的交线，并写出作图步骤，保留作图痕迹．设平面与棱交于点，求三棱锥的体积．

35．如图，在棱长都等于1的三棱锥中，是上的一点，过作平行于棱和棱的截面，分别交，，于，，．

（1）证明截面是矩形；

（2）在的什么位置时，截面面积最大，说明理由．

36．如图，已知三棱柱中，底面，，，，，，分别为棱，的中点．

（1）求异面直线与所成角的大小；

（2）若为线段的中点，试在图中作出过，，三点的平面截该棱柱所得的多边形，并求该截面分三棱柱成两部分（较小部分与较大部分）的体积的比值．

37．已知三棱锥中，与均为等腰直角三角形，且，，为上一点，且平面．

（1）求证：；

（2）过作一平面分别交，，于，，，若四边形为平行四边形，求多面体的表面积．