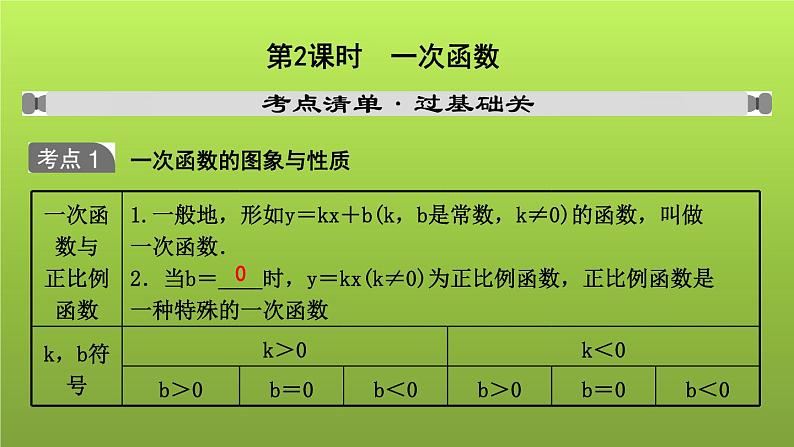
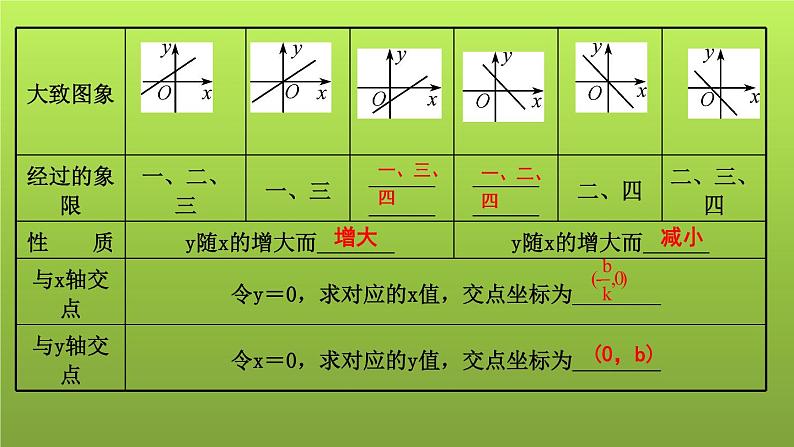






山东省2022年中考数学(五四制)一轮课件:第三章 第2课时 一次函数
展开1.(2020•浙江杭州)在平面直角坐标系中,已知函数y=ax+a(a≠0)的图象过点P(1,2),则该函数的图象可能是( )
2.(2021·潍坊)甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点(0,1);乙:y随x的增大而减小;丙:函数的图象不经过第三象限.根据他们的叙述,写出满足上述性质的一个函数表达式为 .3.(2021·威海模拟)一次函数y=-2x+b,且b>0,则它的图象不经过第 象限.4.(2018·济宁)在平面直角坐标系中,已知一次函数y=-2x+1的图象经过P1(x1,y1),P2(x2,y2)两点,若x1<x2,则y1 y2.(填“>”“<”或“=”)
y=-x+1(答案不唯一,k<0,b=1的一次函数解析式即可)
【划重点】此考点是必考点,是函数中至关重要的考点,是解决一次函数问题的基础与关键点.
3.(2020·贵州黔东南州)把直线y=2x-1向左平移1个单位长度,再向上平移2个单位长度,则平移后所得直线的表达式为 .
4.在平面直角坐标系中,一条直线经过A(-1,5),P(-2,a),B(3,-3)三点.(1)求a的值;(2)设这条直线与y轴相交于点D,求△OPD的面积.解:(1)a=7. (2)S△OPD=3.
一次函数与方程(组)、不等式的关系
1.(2020·济宁)数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( ) A.x=20 B.x=5 C.x=25 D.x=15
2.(2021·湖南娄底)如图,直线y=x+b和y=kx+4与x轴分别相交于点A(-4,0),点B(2,0),则 的解集为( )A.-4
2.(2020·青岛)为让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480 m3,该游泳池有甲、乙两个进水口,注水时每个进水口各自注水速度保持不变,同时打开甲、乙两个进水口注水,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图象如图所示.(1)根据图象求游泳池的蓄水量y(m3)与注水时间t(h)之间的函数关系式,并写出同时打开甲、乙两个进水口的注水速度;(2)现将游泳池的水全部排空,对池内消毒后再重新注水.已知单独打开甲进水口注满游泳池所用时间是单独打开乙进水口注满游泳池所用时间的 倍,求单独打开甲进水口注满游泳池需多少小时?
解:(1)函数关系式为y=140t+100,同时打开甲、乙两个进水口的注水速度为140 m3/h.(2)单独打开甲进水口注满游泳池需8 h.
3.已知A,B两地之间有一条长270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从A地匀速开往B地,乙车从B地沿此公路匀速开往A地,两车分别到达目的地后停止.甲、乙两车相距的路程y(千米)与甲车的行驶时间x(小时)之间的函数关系如图所示.(1)乙车的速度为 千米/时,a= ,b= ;(2)求甲、乙两车相遇后y与x之间的函数关系式;(3)当甲车到达距B地70千米处时,求甲、乙两车之间的路程.
4.(2020•东营)2020年初,新型冠状病毒肺炎疫情暴发,市场上防疫口罩热销,某医药公司每月生产甲、乙两种型号的防疫口罩共20万只,且所有口罩当月全部售出,其中成本、售价如下表:
(1)若该公司三月份的销售收入为300万元,求生产甲、乙两种型号的防疫口罩分别是多少万只? (2)如果公司四月份投入成本不超过216万元,应怎样安排甲、乙两种型号防疫口罩的产量,可使该月公司所获利润最大?并求出最大利润.
解:(1)甲、乙两种型号口罩的产量分别为15万只和5万只.(2)安排生产甲种型号的口罩17万只,乙种型号的口罩3万只时,获得最大利润,最大利润为108万元.
如图,在平面直角坐标系xOy中,过点A(-2,0)的直线交y轴正半轴于点B,将直线AB绕着点O顺时针旋转90°后,分别与x轴,y轴交于点D,C.(1)若OB=4,求直线AB的函数表达式;(2)连接BD,若△ABD的面积是5,求点B的运动路径长.
【思路分析】 (1)依题意求出点B坐标,然后用待定系数法求表达式;(2)设OB=m,则AD=m+2,根据三角形面积公式得到关于m的方程,解方程求得m的值,然后根据弧长公式即可求得.
【方法点拨】 用待定系数法求一次函数的表达式有两种情况:(1)已知两点坐标(或两组对应值)可列方程组求表达式.(2)已知b或k的值,只需一点坐标(或一组对应值)即可.特别地,一次函数发生平移时,平移前后k的值不发生变化.(3)一次函数与几何图形的综合问题,首先应结合图形,分析题干中的已知条件,然后利用几何图形上点的坐标、点之间的距离、图形周长及面积计算方法、特殊图形的性质等,建立函数表达式,求出点的坐标,并考虑全面,从而正确获解.
【问题情境1——示例】1.在弹性限度内,弹簧伸长的长度与所挂物体的重量成正比,某弹簧能挂的重物不超过10 kg,且挂重6 kg时,弹簧长度为13 cm,挂重2 kg时,弹簧的长度为11 cm,求弹簧挂重后的长度y(单位:cm)与所挂重物x(单位:kg)之间的函数关系式,并画出这个函数的图象.
【问题情境2——示例】2.如图,线段AB,CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.(1)写出图中线段CD上点M的坐标及其表示的实际意义;(2)求出客车行驶前油箱内的油量;(3)如果两车同时从相距300千米的甲、乙两地出发,相向而行,匀速行驶,已知轿车的行驶速度比客车的行驶速度快30千米/小时,且当两车在途中相遇时,它们油箱中所剩余的油量恰好相等,求两车的行驶速度.
解:(1)M(1,60),行驶1小时后油箱内还有60升的油. (2)90升. (3)客车的速度为60千米/小时,轿车的速度为90千米/小时.
中考数学复习第三章函数第10课时一次函数课件: 这是一份中考数学复习第三章函数第10课时一次函数课件,共60页。PPT课件主要包含了课前循环练,新课标,考点梳理,广东中考,高分击破,中考演练,命题趋势,平行四边形,①②⑤⑥,x<1等内容,欢迎下载使用。
中考数学复习第三章函数第10课时一次函数课件: 这是一份中考数学复习第三章函数第10课时一次函数课件,共17页。PPT课件主要包含了y=x+1,答案不唯一,a<2等内容,欢迎下载使用。
中考数学总复习第三章第12课时一次函数课件: 这是一份中考数学总复习第三章第12课时一次函数课件,共44页。PPT课件主要包含了y=kxk≠0,故与x轴的交,答案0b,答案1+,答案相等,答案2,0-3,答案y=2x,正比例函数,Ax=等内容,欢迎下载使用。












