中考数学复习第三章函数第10课时一次函数课件

这是一份中考数学复习第三章函数第10课时一次函数课件，共60页。PPT课件主要包含了课前循环练，新课标，考点梳理，广东中考，高分击破，中考演练，命题趋势，平行四边形，①②⑤⑥，x＜1等内容，欢迎下载使用。

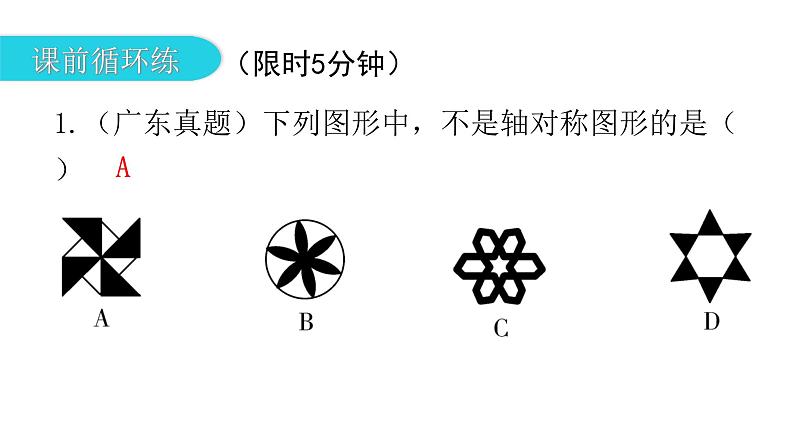
1.（广东真题）下列图形中，不是轴对称图形的是（ ）
2.（广东真题）下列等式正确的是（ ）A.（-1）-3＝1B.（-4）0＝1C.（-2）2×（-2）3＝-26D.（-5）4÷（-5）2＝-52
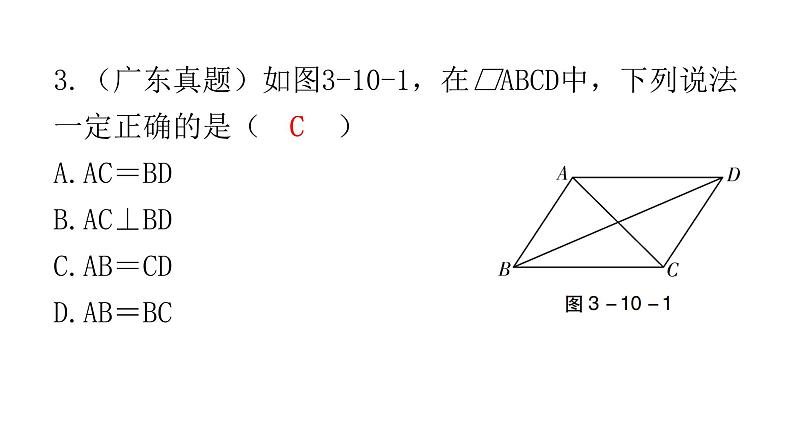
3.（广东真题）如图3-10-1，在□ABCD中，下列说法一定正确的是（ ）A.AC＝BDB.AC⊥BDC.AB＝CDD.AB＝BC
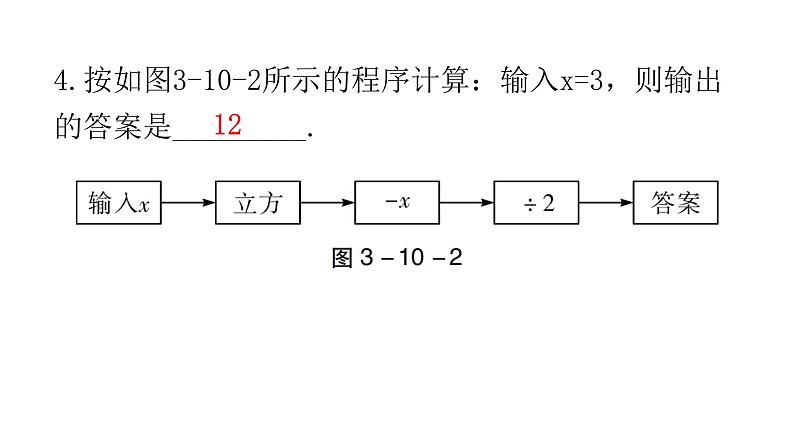
4.按如图3-10-2所示的程序计算：输入x=3，则输出的答案是_________.
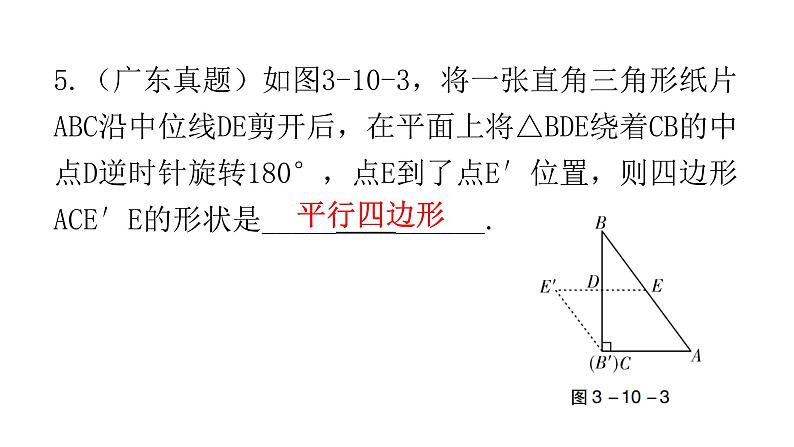
5.（广东真题）如图3-10-3，将一张直角三角形纸片ABC沿中位线DE剪开后，在平面上将△BDE绕着CB的中点D逆时针旋转180°，点E到了点E′位置，则四边形ACE′E的形状是_____ ______.
①结合具体情境体会一次函数的意义，能根据已知条件确定一次函数的表达式；会运用待定系数法确定一次函数的表达式.②能画一次函数的图象，根据图象和函数表达式y=kx+b（k≠0）探索并理解k＞0和k＜0时图象的变化情况；理解正比例函数.③体会一次函数与二元一次方程的关系.④能用一次函数解决简单实际问题.
人教：八下第十九章 一次函数北师：八上第四章 一次函数
1.一次函数与正比例函数（1）一次函数：形如 y=kx+b（k，b 为常数，k≠0）的函数，叫做一次函数.（2）正比例函数：在一次函数y=kx+b（k，b 是常数，k≠0）中，当___________时，它是一个正比例函数，即正比例函数是一种___________的一次函数
2.一次函数的图象与性质
例2.已知一次函数 y=(4m+1)x-(m+1).（1）当m取何值时，y 随 x 的增大而减小?（2）当m取何值时，一次函数的图象与 y 轴的交点在 x 轴的下方?（3）当m取何值时，一次函数的图象经过第二、三、四象限?
3.用待定系数法确定一次函数解析式用待定系数法确定一次函数解析式的一般步骤：（1）设：设出一次函数解析式的一般形式y=kx+b；（2）列：将已知点的坐标代入函数解析式，得到方程（组）；（3）解：解方程（组），求出待定系数的值，写出一次函数解析式
例3.已知一次函数的图象经过 A(-2,-3)，B(1,3)两点，求这个一次函数的表达式.
（3）与一元一次不等式的关系：一次函数y=kx+b的函数值y＞0时，自变量x的取值范围是不等式kx+b＞0的解集；一次函数y=kx+b的函数值y＜0时，自变量x的取值范围是不等式kx+b＜0的解集
5.一次函数在实际问题中的应用解一次函数应用题的一般步骤：（1）找出问题中的变量和常量及它们之间的函数关系； （2）列一次函数表达式表示它们之间的关系； （3）应用一次函数的图象及性质解题； （4）检验结果的合理性，检验是否符合实际意义
例5.如图3-10-5，一个弹簧不挂重物时长6 cm，挂上重物后，在弹性限度内弹簧伸长的长度与所挂重物的质量成正比．弹簧总长y（cm）关于所挂物体质量x（kg）的函数图象如图所示，则图中a的值是（ ）A.3B.4 C.5D.6
1.（2022·广东,函数的表示方法；一次函数关系式）物理实验证实：在弹性限度内，某弹簧长度y（cm）与所挂物体质量x（kg）满足函数关系y＝kx+15.下表是测量物体质量时，该弹簧长度y与所挂物体质量x的数量关系.
（1）求y与x的函数关系式；（2）当弹簧长度为20 cm时，求所挂物体的质量.
解：（1）把x＝2，y＝19代入y＝kx+15，得2k+15=19.解得k＝2.∴y与x的函数关系式为y＝2x+15.（2）把y＝20代入y＝2x+15，得2x+15=20.解得x＝2.5.∴当弹簧长度为20 cm时，所挂物体的质量为2.5 kg.
3.（2020·深圳，一次函数的应用；一元一次方程的应用；一元一次不等式的应用）端午节前夕，某商铺用620元购进50个肉粽和30个蜜枣粽，肉粽的进货单价比蜜枣粽的进货单价多6元.（1）肉粽和蜜枣粽的进货单价分别是多少元？（2）由于粽子畅销，商铺决定再购进这两种粽子共300个，其中肉粽数量不多于蜜枣粽数量的2倍，且每种粽子的进货单价保持不变.若肉粽的销售单价为14元，蜜枣粽的销售单价为6元，试问第二批购进肉粽多少个时，全部售完后，第二批粽子获得的利润最大？最大利润是多少元？
解：（1）设蜜枣粽的进货单价是x元，则肉粽的进货单价是（x+6）元.由题意，得50（x+6）+30x＝620.解得x＝4.则x+6＝10.答：蜜枣粽的进货单价是4元，肉粽的进货单价是10元.
（2）设第二批购进肉粽y个，则购进蜜枣粽（300-y）个，获得利润为w元.由题意，得w＝（14-10）y+（6-4）（300-y）＝2y+600.∵2＞0，∴w随y的增大而增大.∵y≤2（300-y），∴y≤200.∴当y＝200时，w有最大值，w最大值＝2×200+600＝1 000.答：第二批购进肉粽200个时，全部售完后，第二批粽子获得的利润最大，最大利润是1 000元.
1.（2022·广东改编）地表以下岩层的温度y（℃）随着所处深度x（km）的变化而变化.在某个地点y与x之间有如下关系：
已知y与x之间满足一次函数关系.
（1）求y与x的函数关系式；（2）估计地表以下岩层的温度为230 ℃时，岩层所处的深度.
（2）把y＝230代入y=35x+20，得35x+20=230.··7分（代入 数值得1分）解得x＝6.··················8分（解方程得1分）∴估计地表以下岩层的温度为230 ℃时，岩层所处的深度为6 km. ·················9分（写出答案得1分）
温馨提示：此类考题常见于广东省中考数学试卷的第21小题，分值一般为9分，答题时要注意书写格式，分步书写，慢做会求全对，评卷老师是分步给分的哦！
【典型错例】不会用绝对值表示距离和忽视分类讨论
2. 在平面直角坐标系xOy中，直线y＝kx+b过点A（-6，0），且与y轴交于点B，直线与两坐标轴围成的△AOB的面积为12，求直线的函数解析式.
【变式考点】一次函数图象上点的坐标特征
3. （2022·铜仁）在平面直角坐标系内有三点A（-1，4），B（-3，2），C（0，6）. （1）求过其中两点的直线的函数表达式（选一种情形作答）；（2）判断A，B，C三点是否在同一直线上，并说明理由.
【创新考点】一次函数与翻折变换（折叠问题）
4. （2022·凉山州）一次函数y＝3x+b（b≥0）的图象一定不经过（ ）A. 第一象限B. 第二象限C. 第三象限D. 第四象限
5. （2022·临沂）甲、乙两车从A城出发前往B城，在整个行程中，汽车离开A城的距离y（km）与时间x（h）的对应关系如图3-10-7所示.下列说法不正确的是（ ）A. 甲车行驶到距A城240 km处， 被乙车追上B. A城与B城的距离是300 kmC. 乙车的平均速度是80 km/hD. 甲车比乙车早到B城
二、填空题6. （2022·永州）已知一次函数y＝x+1的图象经过点（m，2），则m＝________. 7. （2022·梧州）在平面直角坐标系中，请写出直线y＝2x上的一个点的坐标__ __________________. 8. （2022·泰州）一次函数y＝ax+2的图象经过点（1，0）. 当y＞0时，x的取值范围是___________.
（1，2）(答案不唯一)
三、解答题9. （2022·北京）在平面直角坐标系xOy中，函数y＝kx+b（k≠0）的图象过点（4，3）和（-2，0），且与y轴交于点A. （1）求该函数的解析式及点A的坐标；（2）当x＞0时，对于x的每一个值，函数y＝x+n的值大于函数y＝kx+b（k≠0）的值，直接写出n的取值范围.
10. （2022·陕西）如图3-10-8是一个“函数求值机”的示意图，其中y是x的函数. 下面表格中，是通过该“函数求值机”得到的几组x与y的对应值.
根据以上信息，解答下列问题：（1）当输入x的值为1时，输出y的值为______；（2）求k，b的值；（3）当输出的y值为0时，求输入的x值.
（3）对于y＝8x，当y=0时，得8x=0，解得x＝0.不合题意，舍去；对于y＝2x+6，当y=0时，得2x+6=0.解得x＝-3. 综上所述，当输出的y值为0时，输入的x值为-3.