山东省2022年中考数学（五四制）一轮课件：第四章 第4课时 全等三角形

这是一份山东省2022年中考数学（五四制）一轮课件：第四章 第4课时 全等三角形，共21页。PPT课件主要包含了对应边，对应角，SSS，ASA，SAS，AAS，全等三角形的判定方法，规范解答等内容，欢迎下载使用。

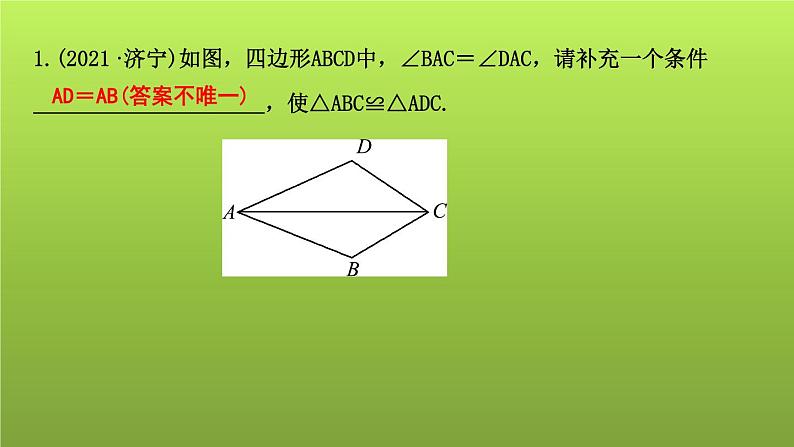
1.(2021·济宁)如图，四边形ABCD中，∠BAC＝∠DAC，请补充一个条件 ，使△ABC≌△ADC.
AD＝AB(答案不唯一)
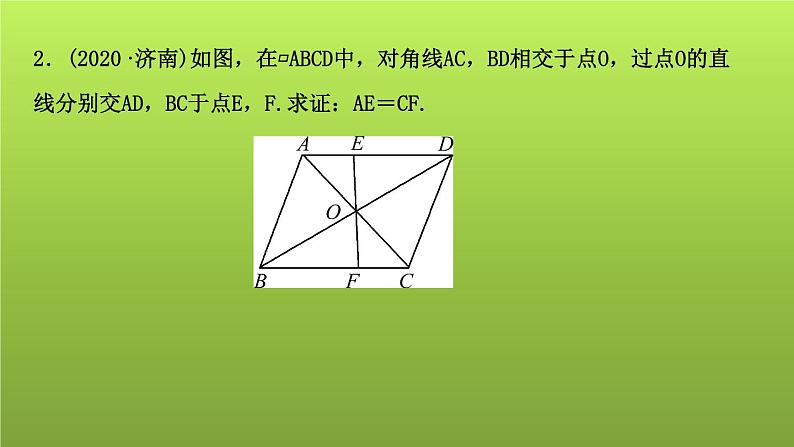
2．(2020·济南)如图，在▱ABCD中，对角线AC，BD相交于点O，过点O的直线分别交AD，BC于点E，F.求证：AE＝CF.
证明：∵四边形ABCD是平行四边形，∴AE∥CF，OA＝OC，∴∠EAO＝∠FCO，∠AEO＝∠CFO，∴△AOE≌△COF，∴AE＝CF.
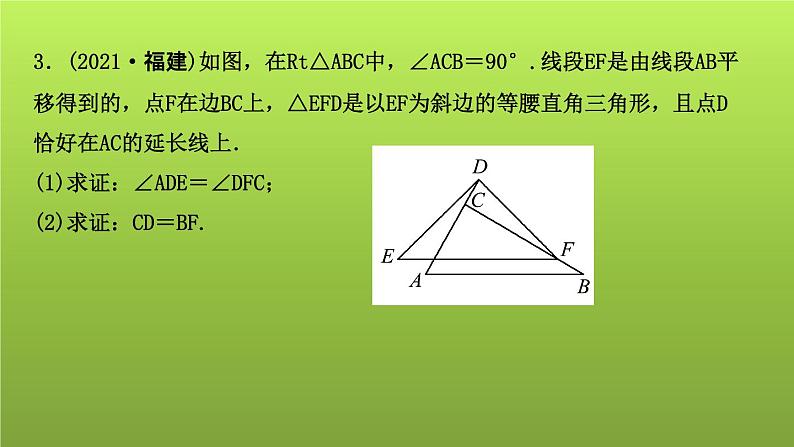
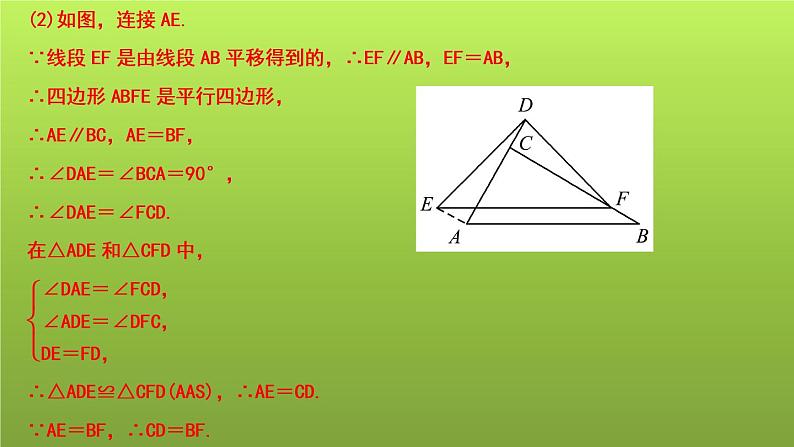
3．(2021·福建)如图，在Rt△ABC中，∠ACB＝90°.线段EF是由线段AB平移得到的，点F在边BC上，△EFD是以EF为斜边的等腰直角三角形，且点D恰好在AC的延长线上．(1)求证：∠ADE＝∠DFC；(2)求证：CD＝BF.
证明：(1)∵∠ACB＝90°，∴∠CDF＋∠DFC＝∠ACB＝90°.∵△EFD是以EF为斜边的等腰直角三角形，∴∠EDF＝90°，DE＝FD.∵∠EDF＝∠ADE＋∠CDF＝90°，∴∠ADE＝∠DFC.
4.(2021·北京)如图，在△ABC中，AB＝AC，∠BAC＝α，点M为BC的中点，点D在MC上，以点A为中心，将线段AD顺时针旋转α得到线段AE，连接BE，DE.(1)比较∠BAE与∠CAD的大小；用等式表示线段BE，BM，MD之间的数量关系，并证明；(2)过点M作AB的垂线，交DE于点N，用等式表示线段NE与ND的数量关系，并证明.
解：(1)∠BAE＝∠CAD，BM＝MD＋BE.证明如下：∵∠BAC＝∠EAD＝α，∴∠BAE＋∠BAD＝∠BAD＋∠CAD＝α，∴∠BAE＝∠CAD.由旋转的性质可得AE＝AD.∵AB＝AC，∴△ABE≌△ACD(SAS)，∴BE＝CD.∵点M为BC的中点，∴BM＝CM.∵CM＝MD＋CD＝MD＋BE，∴BM＝MD＋BE.
(2)ND＝NE.证明如下：如图，过点E作EH⊥AB，垂足为Q，交BC于点H，∴∠EQB＝∠HQB＝90°.由(1)可得△ABE≌△ACD，∴∠ABE＝∠ACD，BE＝CD.
(2020·菏泽)如图，在△ABC中，∠ACB＝90°，点E在AC的延长线上，ED⊥AB于点D.若BC＝ED，求证：CE＝DB.
【思路分析】 根据全等三角形的判定定理(AAS)进行证明即可．
如图，点B，A，D，E在同一直线上，BD＝AE，BC∥EF，∠C＝∠F.求证：AC＝DF.【思路分析】 根据全等三角形的判定定理(AAS)进行证明即可．
如图，C是线段AB上任意一点，分别以AC，BC为边在AB的同侧作等边△ACD和等边△BCE，分别连接AE，BD.求证：AE＝DB.【思路分析】根据全等三角形的判定定理(SAS)进行证明即可．
【规范解答】 证明：∵△ACD和△BCE均是等边三角形，∴AC＝DC，EC＝BC，∠ACD＝∠BCE＝60°.∴∠ACD＋∠DCE＝∠BCE＋∠DCE，∴∠ACE＝∠DCB，∴△ACE≌△DCB，∴AE＝DB.
【问题情境——示例】一块三角形的玻璃摔碎成如图所示的四块，小亮现在要带其中的一块去配成与原来一样大小的三角形玻璃，小亮去时应该带( )　　　　A．第一块 B．第二块C．第三块 D．第四块