人教版八年级上册11.3.1 多边形第一课时学案设计

3　多边形及其内角和

第1课时　多边形导学案

学习目标

1.了解多边形的有关概念.

2.了解正多边形的基本性质.

学习策略

1.结合图形总结多边形对角线条数的计算方法；

2.牢记正多边形的概念.

学习过程 

一.复习回顾：

问题:观察下面的图片,你能找到哪些我们熟悉的图形?

二.新课学习：

探究1:观察多边形的构成,类比三角形的有关概念探索多边形的有关概念

1.观察画多边形的过程,类比三角形的概念,你能说出什么是多边形吗?

2.观察这个多边形,为什么有一条边是虚线?

3.根据图示,类比三角形的有关概念,说明什么是多边形的边、顶点、内角、外角和对角线.

4.三角形有对角线吗?为什么?

5.回想三角形的表示方法,多边形应如何表示?

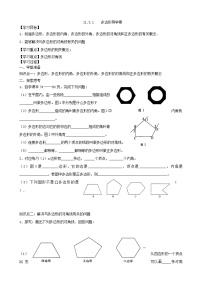
6.如图所示,观察两个图形,找出相同点和不同点.

探究2:自主探索正多边形的概念及基本性质

1.观察下列图形,它们的边、角有什么特点?

2.     像这样的多边形我们称为正多边形.请用自己的语言说明什么是正多边形?

3.下面的叙述是否正确?(正确的请说明理由,错误的请举出反例.)

(1)各个角都相等的多边形叫做正多边形.

(2)各条边都相等的多边形叫做正多边形.

4.由定义可知,正多边形有什么性质?

三.尝试应用：

1.判断题.

(1)由四条线段首尾顺次相接组成的图形叫四边形. (   )

(2)由不在一条直线上的四条线段首尾顺次相接组成的图形叫四边形. (   )

(3)由不在一条直线上的四条线段首尾顺次相接组成的图形,且其中任何一条线段所在的直线使整个图形都在这条直线的同一侧,叫做四边形.(   )

(4)在同一平面内,由四条线段首尾顺次相接组成的封闭图形叫四边形. (   )

2.填空题.

(1)连接多边形             的线段,叫做多边形的对角线. 

(2)多边形的任何              所在的直线,整个多边形都在这条直线的            ,这样的多边形叫凸多边形. 

(3)各个角              ,各条边            的多边形,叫正多边形. 

(4)一个n边形有             条边,              个顶点,                个内角,              个外角. 

3.从一个顶点出发,四边形可以画1条对角线,将四边形分成2个三角形;五边形可以画          条对角线,将五边形分成         个三角形;六边形可以画          条对角线,将六边形分成            个三角形……n边形可以画           条对角线,将n边形分成           个三角形. 

4.填表:

5.画出下列多边形的全部对角线.

四.自主总结：

1.在         内.由一些线段              相接组成的封闭图形叫做多边形.画出多边形的任何一条边所在的直线，如果整个多边形都在这条直线的             .那么这个多边形叫做凸多边形.

2.连接多边形                 的两个顶点的线段.叫做多边形的对角线.从n边形（n＞3）一个顶点出发引对角线.有______________条.

3.各个角            ,各条边           的多边形叫做正多边形.

五.达标测试

一、选择题

1.从一个多边形的任何一个顶点出发都只有6条对角线，则它的边数是（　　）

A．6 B．7 C．8 D．9

2.如图，把边长是15cm的正三角形纸板，剪去三个小正三角形后，得到一个正六边形，则剪去的小正三角形的边长是（　　）

A．3cm B．4cm C．5cm D．6cm

3.下列属于正多边形的特征的有（　　）

①各边相等；②各个内角相等；

③各个外角相等；④各条对角线相等；

⑤从一个顶点引出的对角线将n边形分成面积相等的（n-2）个三角形．

A．2个 B．3个 C．4个 D．5个

二、填空题

4.一个正多边形的周长是100，边长为10，则正多边形的边数n═________．

5.过某个多边形的一个顶点的所有对角线，将这个多边形分成6个三角形，这个多边形是_________边形．

6.如图所示，将多边形分割成三角形、图（1）中可分割出2个三角形；图（2）中可分割出3个三角形；图（3）中可分割出4个三角形；由此你能猜测出，n边形可以分割出__________个三角形．

三、解答题

7.若一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍，求此多边形的边数．

8.已知从n边形的一个顶点出发共有4条对角线，其周长为56，且各边长是连续的自然数，求这个多边形的各边长．

9.在如图所示的四边形中，截去一个角后，使它变成：(1)三角形;(2)四边形；(3)五边形.请在图中画出截线.

10.分别画出下列各多边形的对角线，并观察图形完成下列问题：
（1）试写出用n边形的边数n表示对角线总条数S的式子：_________________．
（2）从十五边形的一个顶点可以引出_________条对角线，十五边形共有____________条对角线：
（3）如果一个多边形对角线的条数与它的边数相等，求这个多边形的边数．

参考答案

1.D  解析：设多边形有n条边，则n-3=6，解得n=9．

2.C  解析：∵剪去三个三角形，得到正六边形，∴剪去的三个三角形是全等的等边三角形；且被剪的正三角形的边长为15cm，∴剪去的小正三角形的边长=5cm．

3.B  解析：①各边相等是正确的；②各个内角相等是正确的；③各个外角相等是正确的；④各条对角线不一定相等，原来的说法是错误的；⑤从一个顶点引出的对角线将n边形分成面积不一定相等的（n-2）个三角形，原来的说法是错误的．

4.10  解析：∵正多边形的周长是100，边长为10，∴正多边形的边数n= =10.

5.八  解析：设多边形是n边形，由对角线公式，得n-2=6．解得n=8.

6.（n-1）  解析：n边形可以分割出（n-1）个三角形．

7.解：设此多边形有n条边，由题意，得n=2（n-3），解得n=6．故此多边形有6条边．

8.解：依题意有n-3=4，解得n=7，设最短边为x，则7x+1+2+3+4+5+6=56，解得x=5．故这个多边形的各边长是5，6，7，8，9，10，11．

9.解：答案不唯一，例如下图.

10.解：（1）用n边形的边数n表示对角线总条数S的式子：S=n（n-3）；（2）十五边形从一个顶点可引出对角线：15-3=12（条），共有对角线：×15×（15-3）=90（条）；（3）设多边形有n条边，则n（n-3）=n，解得n=5．故这个多边形的边数是5．故答案为：S=n（n-3）；12，90．