06解答题容易题&基础题知识点分类-浙江省2022年各地区中考数学真题分类汇编

这是一份06解答题容易题&基础题知识点分类-浙江省2022年各地区中考数学真题分类汇编，共42页。试卷主要包含了﹣23，计算，，其中x＝，观察下面的等式，0+2﹣1，解方程组，0﹣，2+3﹣2﹣|﹣|等内容，欢迎下载使用。

06解答题容易题&基础题知识点分类-浙江省2022年各地区中考数学真题分类汇编
一．有理数的混合运算（共1小题）
1．（2022•杭州）计算：（﹣6）×（﹣■）﹣23．
圆圆在做作业时，发现题中有一个数字被墨水污染了．
（1）如果被污染的数字是，请计算（﹣6）×（﹣）﹣23．
（2）如果计算结果等于6，求被污染的数字．
二．实数的运算（共2小题）
2．（2022•台州）计算：+|﹣5|﹣22．
3．（2022•湖州）计算：（）2+2×（﹣3）．
三．整式的混合运算—化简求值（共1小题）
4．（2022•丽水）先化简，再求值：（1+x）（1﹣x）+x（x+2），其中x＝．
四．分式的加减法（共1小题）
5．（2022•舟山）观察下面的等式：＝+，＝+，＝+，……
（1）按上面的规律归纳出一个一般的结论（用含n的等式表示，n为正整数）．
（2）请运用分式的有关知识，推理说明这个结论是正确的．
五．负整数指数幂（共1小题）
6．（2022•丽水）计算：﹣（﹣2022）0+2﹣1．
六．解二元一次方程组（共1小题）
7．（2022•台州）解方程组：．
七．解分式方程（共1小题）
8．（2022•嘉兴）（1）计算：（1﹣）0﹣．
（2）解方程：＝1．
八．解一元一次不等式（共2小题）
9．（2022•温州）（1）计算：+（﹣3）2+3﹣2﹣|﹣|．
（2）解不等式9x﹣2≤7x+3，并把解集表示在数轴上．

10．（2022•舟山）（1）计算：﹣（﹣1）0．
（2）解不等式：x+8＜4x﹣1．
九．解一元一次不等式组（共2小题）
11．（2022•湖州）解一元一次不等式组．
12．（2022•宁波）（1）计算：（x+1）（x﹣1）+x（2﹣x）．
（2）解不等式组：．
一十．函数的图象（共1小题）
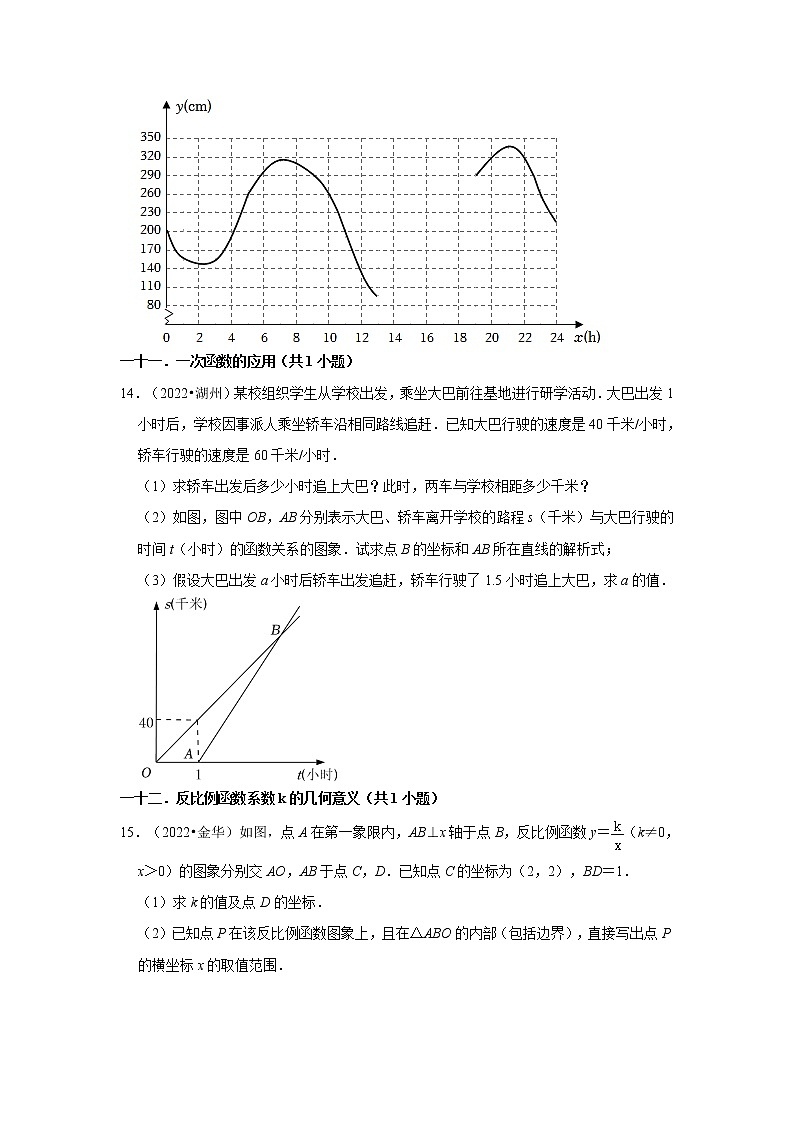
13．（2022•舟山）6月13日，某港口的湖水高度y（cm）和时间x（h）的部分数据及函数图象如下：
x（h）
…
11
12
13
14
15
16
17
18
…
y（cm）
…
189
137
103
80
101
133
202
260
…
（数据来自某海洋研究所）
（1）数学活动：
①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图象．
②观察函数图象，当x＝4时，y的值为多少？当y的值最大时，x的值为多少？
（2）数学思考：
请结合函数图象，写出该函数的两条性质或结论．
（3）数学应用：
根据研究，当潮水高度超过260cm时，货轮能够安全进出该港口．请问当天什么时间段适合货轮进出此港口？
一十一．一次函数的应用（共1小题）
14．（2022•湖州）某校组织学生从学校出发，乘坐大巴前往基地进行研学活动．大巴出发1小时后，学校因事派人乘坐轿车沿相同路线追赶．已知大巴行驶的速度是40千米/小时，轿车行驶的速度是60千米/小时．
（1）求轿车出发后多少小时追上大巴？此时，两车与学校相距多少千米？
（2）如图，图中OB，AB分别表示大巴、轿车离开学校的路程s（千米）与大巴行驶的时间t（小时）的函数关系的图象．试求点B的坐标和AB所在直线的解析式；
（3）假设大巴出发a小时后轿车出发追赶，轿车行驶了1.5小时追上大巴，求a的值．

一十二．反比例函数系数k的几何意义（共1小题）
15．（2022•金华）如图，点A在第一象限内，AB⊥x轴于点B，反比例函数y＝（k≠0，x＞0）的图象分别交AO，AB于点C，D．已知点C的坐标为（2，2），BD＝1．
（1）求k的值及点D的坐标．
（2）已知点P在该反比例函数图象上，且在△ABO的内部（包括边界），直接写出点P的横坐标x的取值范围．

一十三．待定系数法求反比例函数解析式（共1小题）
16．（2022•温州）已知反比例函数y＝（k≠0）的图象的一支如图所示，它经过点（3，﹣2）．
（1）求这个反比例函数的表达式，并补画该函数图象的另一支．
（2）求当y≤5，且y≠0时自变量x的取值范围．

一十四．二次函数的应用（共1小题）
17．（2022•宁波）为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y千克与每平方米种植的株数x（2≤x≤8，且x为整数）构成一种函数关系．每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克．
（1）求y关于x的函数表达式．
（2）每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？
一十五．等腰三角形的判定与性质（共1小题）
18．（2022•温州）如图，BD是△ABC的角平分线，DE∥BC，交AB于点E．
（1）求证：∠EBD＝∠EDB．
（2）当AB＝AC时，请判断CD与ED的大小关系，并说明理由．

一十六．直角三角形斜边上的中线（共1小题）
19．（2022•杭州）如图，在Rt△ACB中，∠ACB＝90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A＝50°，∠ACE＝30°．
（1）求证：CE＝CM．
（2）若AB＝4，求线段FC的长．

一十七．勾股定理（共1小题）
20．（2022•金华）如图1，将长为2a+3，宽为2a的矩形分割成四个全等的直角三角形，拼成“赵爽弦图”（如图2），得到大小两个正方形．
（1）用关于a的代数式表示图2中小正方形的边长．
（2）当a＝3时，该小正方形的面积是多少？

一十八．菱形的判定（共1小题）
21．（2022•舟山）小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB＝OD．求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．
小惠：
证明：∵AC⊥BD，OB＝OD，
∴AC垂直平分BD．
∴AB＝AD，CB＝CD，
∴四边形ABCD是菱形．
小洁：
这个题目还缺少条件，需要补充一个条件才能证明．
若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．

一十九．矩形的判定与性质（共1小题）
22．（2022•湖州）如图，已知在Rt△ABC中，∠C＝Rt∠，D是AB边上一点，以BD为直径的半圆O与边AC相切，切点为E，过点O作OF⊥BC，垂足为F．
（1）求证：OF＝EC；
（2）若∠A＝30°，BD＝2，求AD的长．

二十．切线的性质（共1小题）
23．（2022•绍兴）如图，半径为6的⊙O与Rt△ABC的边AB相切于点A，交边BC于点C，D，∠B＝90°，连结OD，AD．
（1）若∠ACB＝20°，求的长（结果保留π）．
（2）求证：AD平分∠BDO．

二十一．圆的综合题（共1小题）
24．（2022•台州）如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC交于点D，连接AD．
（1）求证：BD＝CD．
（2）若⊙O与AC相切，求∠B的度数．
（3）用无刻度的直尺和圆规作出劣弧的中点E．（不写作法，保留作图痕迹）

二十二．作图—复杂作图（共2小题）
25．（2022•宁波）图1，图2都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点，线段AB的端点均在格点上，分别按要求画出图形．
（1）在图1中画出等腰三角形ABC，且点C在格点上．（画出一个即可）
（2）在图2中画出以AB为边的菱形ABDE，且点D，E均在格点上．


26．（2022•丽水）如图，在6×6的方格纸中，点A，B，C均在格点上，试按要求画出相应格点图形．

（1）如图1，作一条线段，使它是AB向右平移一格后的图形；
（2）如图2，作一个轴对称图形，使AB和AC是它的两条边；
（3）如图3，作一个与△ABC相似的三角形，相似比不等于1．

二十三．作图-旋转变换（共1小题）
27．（2022•温州）如图，在2×6的方格纸中，已知格点P，请按要求画格点图形（顶点均在格点上）．
（1）在图1中画一个锐角三角形，使P为其中一边的中点，再画出该三角形向右平移2个单位后的图形．
（2）在图2中画一个以P为一个顶点的钝角三角形，使三边长都不相等，再画出该三角形绕点P旋转180°后的图形．

二十四．锐角三角函数的定义（共1小题）
28．（2022•湖州）如图，已知在Rt△ABC中，∠C＝Rt∠，AB＝5，BC＝3．求AC的长和sinA的值．

二十五．特殊角的三角函数值（共1小题）
29．（2022•金华）计算：（﹣2022）0﹣2tan45°+|﹣2|+．
二十六．解直角三角形的应用（共1小题）
30．（2022•绍兴）圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．图2是一个根据某市地理位置设计的圭表平面示意图，表AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37°，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．

（1）求∠BAD的度数．
（2）求表AC的长（最后结果精确到0.1米）．
（参考数据：sin37°≈，cos37°≈，tan37°≈，tan84°≈）
二十七．解直角三角形的应用-坡度坡角问题（共1小题）
31．（2022•台州）如图1，梯子斜靠在竖直的墙上，其示意图如图2．梯子与地面所成的角α为75°，梯子AB长3m，求梯子顶部离地竖直高度BC．（结果精确到0.1m；参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

二十八．频数（率）分布表（共1小题）
32．（2022•温州）为了解某校400名学生在校午餐所需的时间，抽查了20名学生在校午餐所花的时间，由图示分组信息得：A，C，B，B，C，C，C，A，B，C，C，C，D，B，C，C，C，E，C，C．
分组信息
A组：5＜x≤10
B组：10＜x≤15
C组：15＜x≤20
D组：20＜x≤25
E组：25＜x≤30
注：x（分钟）为午餐时间！
某校被抽查的20名学生在校午餐所花时间的频数表
组别
划记
频数
A

2
B

4
C
　 　
　 　
D
　 　
　 　
E
　 　
　 　
合计
20
（1）请填写频数表，并估计这400名学生午餐所花时间在C组的人数．
（2）在既考虑学生午餐用时需求，又考虑食堂运行效率的情况下，校方准备在15分钟，20分钟，25分钟，30分钟中选择一个作为午餐时间，你认为应选择几分钟为宜？说明理由．


二十九．扇形统计图（共3小题）
33．（2022•绍兴）双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长x（单位：小时）的情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．
八年级学生每日完成书面作业所需时长情况的统计表
组别
所需时长（小时）
学生人数（人）
A
0＜x≤0.5
15
B
0.5＜x≤1
m
C
1＜x≤1.5
n
D
1.5＜x≤2
5
（1）求统计表中m，n的值．
（2）已知该校八年级学生有800人，试估计该校八年级学生中每日完成书面作业所需时长满足0.5＜x≤1.5的共有多少人．

34．（2022•台州）某中学为加强学生的劳动教育，需要制定学生每周劳动时间（单位：小时）的合格标准，为此随机调查了100名学生目前每周劳动时间，获得数据并整理成下表．
学生目前每周劳动时间统计表
每周劳动时间x（小时）
0.5≤x＜1.5
1.5≤x＜2.5
2.5≤x＜3.5
3.5≤x＜4.5
4.5≤x＜5.5
组中值
1
2
3
4
5
人数（人）
21
30
19
18
12
（1）画扇形图描述数据时，1.5≤x＜2.5这组数据对应的扇形圆心角是多少度？
（2）估计该校学生目前每周劳动时间的平均数．
（3）请你为该校制定一个学生每周劳动时间的合格标准（时间取整数小时），并用统计量说明其合理性．
35．（2022•金华）学校举办演讲比赛，总评成绩由“内容、表达、风度、印象”四部分组成．九（1）班组织选拔赛，制定的各部分所占比例如图，三位同学的成绩如下表．请解答下列问题：
三位同学的成绩统计表

内容
表达
风度
印象
总评成绩
小明
8
7
8
8
m
小亮
7
8
8
9
7.85
小田
7
9
7
7
7.8
（1）求图中表示“内容”的扇形的圆心角度数．
（2）求表中m的值，并根据总评成绩确定三人的排名顺序．
（3）学校要求“内容”比“表达”重要，该统计图中各部分所占比例是否合理？如果不合理，如何调整？

三十．条形统计图（共3小题）
36．（2022•舟山）某教育部门为了解本地区中小学生参加家庭劳动时间的情况，随机抽取该地区1200名中小学生进行问卷调查，并将调查问卷（部分）和结果描述如下：
调查问卷（部分）
1．你每周参加家庭劳动时间大约是______h．
如果你每周参加家庭劳动时间不足2h，请回答第2个问题：
2．影响你每周参加家庭劳动的主要原因是______（单选）．
A．没时间
B．家长不舍得
C．不喜欢
D．其它

中小学生每周参加家庭劳动时间x（h） 分为5组：第一组（0≤x＜0.5），第二组（0.5≤x＜1），第三组（1≤x＜1.5），第四组（1.5≤x＜2），第五组（x≥2）．
根据以上信息，解答下列问题：
（1）本次调查中，中小学生每周参加家庭劳动时间的中位数落在哪一组？
（2）在本次被调查的中小学生中，选择“不喜欢”的人数为多少？
（3）该教育部门倡议本地区中小学生每周参加家庭劳动时间不少于2h．请结合上述统计图，对该地区中小学生每周参加家庭劳动时间的情况作出评价，并提出两条合理化建议．
37．（2022•湖州）为落实“双减”政策，切实减轻学生学业负担，丰富学生课余生活，某校积极开展“五育并举”课外兴趣小组活动，计划成立“爱心传递”、“音乐舞蹈”、“体育运动”、“美工制作”和“劳动体验”五个兴趣小组，要求每位学生都只选其中一个小组．为此，随机抽查了本校各年级部分学生选择兴趣小组的意向，并将抽查结果绘制成如下统计图（不完整）．

根据统计图中的信息，解答下列问题：
（1）求本次被抽查学生的总人数和扇形统计图中表示“美工制作”的扇形的圆心角度数；
（2）将条形统计图补充完整；
（3）该校共有1600名学生，根据抽查结果，试估计全校选择“爱心传递”兴趣小组的学生人数．

38．（2022•丽水）某校为了解学生在“五•一”小长假期间参与家务劳动的时间t（小时），随机抽取了本校部分学生进行问卷调查．要求抽取的学生在A，B，C，D，E五个选项中选且只选一项，并将抽查结果绘制成如下两幅不完整的统计图，请根据图中信息回答问题：

（1）求所抽取的学生总人数；
（2）若该校共有学生1200人，请估算该校学生参与家务劳动的时间满足3≤t＜4的人数；
（3）请你根据调查结果，对该校学生参与家务劳动时间的现状作简短评述．
三十一．折线统计图（共1小题）
39．（2022•宁波）小聪、小明参加了100米跑的5期集训，每期集训结束时进行测试．根据他们集训时间、测试成绩绘制成如下两个统计图．

根据图中信息，解答下列问题：
（1）这5期的集训共有多少天？
（2）哪一期小聪的成绩比他上一期的成绩进步最多？进步了多少秒？
（3）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面，简要说说你的想法．

参考答案与试题解析
一．有理数的混合运算（共1小题）
1．（2022•杭州）计算：（﹣6）×（﹣■）﹣23．
圆圆在做作业时，发现题中有一个数字被墨水污染了．
（1）如果被污染的数字是，请计算（﹣6）×（﹣）﹣23．
（2）如果计算结果等于6，求被污染的数字．
【解答】解：（1）（﹣6）×（﹣）﹣23
＝（﹣6）×﹣8
＝﹣1﹣8
＝﹣9；
（2）设被污染的数字为x，
根据题意得：（﹣6）×（﹣x）﹣23＝6，
解得：x＝3，
答：被污染的数字是3．
二．实数的运算（共2小题）
2．（2022•台州）计算：+|﹣5|﹣22．
【解答】解：+|﹣5|﹣22
＝3+5﹣4
＝8﹣4
＝4．
3．（2022•湖州）计算：（）2+2×（﹣3）．
【解答】解：原式＝6+（﹣6）
＝0．
三．整式的混合运算—化简求值（共1小题）
4．（2022•丽水）先化简，再求值：（1+x）（1﹣x）+x（x+2），其中x＝．
【解答】解：（1+x）（1﹣x）+x（x+2）
＝1﹣x2+x2+2x
＝1+2x，
当x＝时，原式＝1+＝1+1＝2．
四．分式的加减法（共1小题）
5．（2022•舟山）观察下面的等式：＝+，＝+，＝+，……
（1）按上面的规律归纳出一个一般的结论（用含n的等式表示，n为正整数）．
（2）请运用分式的有关知识，推理说明这个结论是正确的．
【解答】解：（1）观察规律可得：＝+；
（2）∵+
＝+
＝
＝，
∴＝+．
五．负整数指数幂（共1小题）
6．（2022•丽水）计算：﹣（﹣2022）0+2﹣1．
【解答】解：原式＝3﹣1+
＝2+
＝．
六．解二元一次方程组（共1小题）
7．（2022•台州）解方程组：．
【解答】解：，
②﹣①得：y＝1，
把y＝1代入①得：x＝2，
∴原方程组的解为．
七．解分式方程（共1小题）
8．（2022•嘉兴）（1）计算：（1﹣）0﹣．
（2）解方程：＝1．
【解答】解：（1）原式＝1﹣2＝﹣1；
（2）去分母得x﹣3＝2x﹣1，
∴﹣x＝3﹣1，
∴x＝﹣2，
经检验x＝﹣2是分式方程的解，
∴原方程的解为：x＝﹣2．
八．解一元一次不等式（共2小题）
9．（2022•温州）（1）计算：+（﹣3）2+3﹣2﹣|﹣|．
（2）解不等式9x﹣2≤7x+3，并把解集表示在数轴上．

【解答】解：（1）+（﹣3）2+3﹣2﹣|﹣|
＝3+9+﹣
＝12；
（2）9x﹣2≤7x+3，
移项，得：9x﹣7x≤3+2，
合并同类项，得：2x≤5，
系数化为1，得：x≤2.5，
其解集在数轴上表示如下：
．
10．（2022•舟山）（1）计算：﹣（﹣1）0．
（2）解不等式：x+8＜4x﹣1．
【解答】解：（1）﹣（﹣1）0
＝2﹣1
＝1；
（2）x+8＜4x﹣1
移项及合并同类项，得：﹣3x＜﹣9，
系数化为1，得：x＞3．
九．解一元一次不等式组（共2小题）
11．（2022•湖州）解一元一次不等式组．
【解答】解：解不等式①得：x＜2，
解不等式②得：x＜1，
∴原不等式组的解集为x＜1．
12．（2022•宁波）（1）计算：（x+1）（x﹣1）+x（2﹣x）．
（2）解不等式组：．
【解答】解：（1）原式＝x2﹣1+2x﹣x2
＝2x﹣1；
（2），
解不等式①得：x＞3，
解不等式②得：x≥﹣2，
∴原不等式组的解集为：x＞3．
一十．函数的图象（共1小题）
13．（2022•舟山）6月13日，某港口的湖水高度y（cm）和时间x（h）的部分数据及函数图象如下：
x（h）
…
11
12
13
14
15
16
17
18
…
y（cm）
…
189
137
103
80
101
133
202
260
…
（数据来自某海洋研究所）
（1）数学活动：
①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图象．
②观察函数图象，当x＝4时，y的值为多少？当y的值最大时，x的值为多少？
（2）数学思考：
请结合函数图象，写出该函数的两条性质或结论．
（3）数学应用：
根据研究，当潮水高度超过260cm时，货轮能够安全进出该港口．请问当天什么时间段适合货轮进出此港口？
【解答】解：（1）①如图：

②通过观察函数图象，当x＝4时，y＝200，当y值最大时，x＝21；
（2）该函数的两条性质如下（答案不唯一）：
①当2≤x≤7时，y随x的增大而增大；
②当x＝14时，y有最小值为80；
（3）由图象，当y＝260时，x＝5或x＝10或x＝18或x＝23，
∴当5＜x＜10或18＜x＜23时，y＞260，
即当5＜x＜10或18＜x＜23时，货轮进出此港口．
一十一．一次函数的应用（共1小题）
14．（2022•湖州）某校组织学生从学校出发，乘坐大巴前往基地进行研学活动．大巴出发1小时后，学校因事派人乘坐轿车沿相同路线追赶．已知大巴行驶的速度是40千米/小时，轿车行驶的速度是60千米/小时．
（1）求轿车出发后多少小时追上大巴？此时，两车与学校相距多少千米？
（2）如图，图中OB，AB分别表示大巴、轿车离开学校的路程s（千米）与大巴行驶的时间t（小时）的函数关系的图象．试求点B的坐标和AB所在直线的解析式；
（3）假设大巴出发a小时后轿车出发追赶，轿车行驶了1.5小时追上大巴，求a的值．

【解答】解：（1）设轿车出发后x小时追上大巴，
依题意得：40（x+1）＝60x，
解得x＝2．
∴轿车出发后2小时追上大巴，
此时，两车与学校相距60×2＝120（千米），
答，轿车出发后2小时追上大巴，此时，两车与学校相距120千米；

（2）∵轿车出发后2小时追上大巴，此时，两车与学校相距120千米，
∴大巴行驶了3小时，
∴B（3，120），
由图象得A（1，0），
设AB所在直线的解析式为y＝kt+b，
∴，
解得，
∴AB所在直线的解析式为y＝60t﹣60；

（3）依题意得：40（a+1.5）＝60×1.5，
解得a＝．
∴a的值为．
一十二．反比例函数系数k的几何意义（共1小题）
15．（2022•金华）如图，点A在第一象限内，AB⊥x轴于点B，反比例函数y＝（k≠0，x＞0）的图象分别交AO，AB于点C，D．已知点C的坐标为（2，2），BD＝1．
（1）求k的值及点D的坐标．
（2）已知点P在该反比例函数图象上，且在△ABO的内部（包括边界），直接写出点P的横坐标x的取值范围．

【解答】解：（1）∵点C（2，2）在反比例函数y＝（k≠0，x＞0）的图象上，
∴2＝，
解得k＝4，
∵BD＝1．
∴点D的纵坐标为1，
∵点D在反比例函数y＝（k≠0，x＞0）的图象上，
∴1＝，
解得x＝4，
即点D的坐标为（4，1）；
（2）∵点C（2，2），点D（4，1），点P在该反比例函数图象上，且在△ABO的内部（包括边界），
∴点P的横坐标x的取值范围是2≤x≤4．
一十三．待定系数法求反比例函数解析式（共1小题）
16．（2022•温州）已知反比例函数y＝（k≠0）的图象的一支如图所示，它经过点（3，﹣2）．
（1）求这个反比例函数的表达式，并补画该函数图象的另一支．
（2）求当y≤5，且y≠0时自变量x的取值范围．

【解答】解：（1）把点（3，﹣2）代入y＝（k≠0），
﹣2＝，
解得：k＝﹣6，
∴反比例函数的表达式为y＝﹣，
补充其函数图象如下：

（2）当y＝5时，﹣＝5，
解得：x＝﹣，
∴当y≤5，且y≠0时，x≤﹣或x＞0．
一十四．二次函数的应用（共1小题）
17．（2022•宁波）为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y千克与每平方米种植的株数x（2≤x≤8，且x为整数）构成一种函数关系．每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克．
（1）求y关于x的函数表达式．
（2）每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？
【解答】解：（1）∵每平方米种植的株数每增加1株，单株产量减少0.5千克，
∴y＝4﹣0.5（x﹣2）＝﹣0.5x+5，
答：y关于x的函数表达式为y＝﹣0.5x+5，（2≤x≤8，且x为整数）；
（2）设每平方米小番茄产量为W千克，
根据题意得：W＝x（﹣0.5x+5）＝﹣0.5x2+5x＝﹣0.5（x﹣5）2+12.5，
∵﹣0.5＜0，
∴当x＝5时，W取最大值，最大值为12.5，
答：每平方米种植5株时，能获得最大的产量，最大产量为12.5千克．
一十五．等腰三角形的判定与性质（共1小题）
18．（2022•温州）如图，BD是△ABC的角平分线，DE∥BC，交AB于点E．
（1）求证：∠EBD＝∠EDB．
（2）当AB＝AC时，请判断CD与ED的大小关系，并说明理由．

【解答】（1）证明：∵BD是△ABC的角平分线，
∴∠CBD＝∠EBD，
∵DE∥BC，
∴∠CBD＝∠EDB，
∴∠EBD＝∠EDB．
（2）解：CD＝ED，理由如下：
∵AB＝AC，
∴∠C＝∠ABC，
∵DE∥BC，
∴∠ADE＝∠C，∠AED＝∠ABC，
∴∠ADE＝∠AED，
∴AD＝AE，
∴CD＝BE，
由（1）得，∠EBD＝∠EDB，
∴BE＝DE，
∴CD＝ED．
一十六．直角三角形斜边上的中线（共1小题）
19．（2022•杭州）如图，在Rt△ACB中，∠ACB＝90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE．已知∠A＝50°，∠ACE＝30°．
（1）求证：CE＝CM．
（2）若AB＝4，求线段FC的长．

【解答】（1）证明：∵∠ACB＝90°，点M为边AB的中点，
∴MC＝MA＝MB，
∴∠MCA＝∠A，∠MCB＝∠B，
∵∠A＝50°，
∴∠MCA＝50°，∠MCB＝∠B＝40°，
∴∠EMC＝∠MCB+∠B＝80°，
∵∠ACE＝30°，
∴∠MEC＝∠A+∠ACE＝80°，
∴∠MEC＝∠EMC，
∴CE＝CM；
（2）解：∵AB＝4，
∴CE＝CM＝AB＝2，
∵EF⊥AC，∠ACE＝30°，
∴FC＝CE•cos30°＝．
一十七．勾股定理（共1小题）
20．（2022•金华）如图1，将长为2a+3，宽为2a的矩形分割成四个全等的直角三角形，拼成“赵爽弦图”（如图2），得到大小两个正方形．
（1）用关于a的代数式表示图2中小正方形的边长．
（2）当a＝3时，该小正方形的面积是多少？

【解答】解：（1）∵直角三角形较短的直角边＝×2a＝a，
较长的直角边＝2a+3，
∴小正方形的边长＝2a+3﹣a＝a+3；
（2）小正方形的面积＝（a+3）2，
当a＝3时，面积＝（3+3）2＝36．
一十八．菱形的判定（共1小题）
21．（2022•舟山）小惠自编一题：“如图，在四边形ABCD中，对角线AC，BD交于点O，AC⊥BD，OB＝OD．求证：四边形ABCD是菱形”，并将自己的证明过程与同学小洁交流．
小惠：
证明：∵AC⊥BD，OB＝OD，
∴AC垂直平分BD．
∴AB＝AD，CB＝CD，
∴四边形ABCD是菱形．
小洁：
这个题目还缺少条件，需要补充一个条件才能证明．
若赞同小惠的证法，请在第一个方框内打“√”；若赞成小洁的说法，请你补充一个条件，并证明．

【解答】解：赞成小洁的说法，补充条件：OA＝OC，证明如下：
∵OA＝OC，OB＝OD，
∴四边形ABCD是平行四边形，
又∵AC⊥BD，
∴平行四边形ABCD是菱形．
一十九．矩形的判定与性质（共1小题）
22．（2022•湖州）如图，已知在Rt△ABC中，∠C＝Rt∠，D是AB边上一点，以BD为直径的半圆O与边AC相切，切点为E，过点O作OF⊥BC，垂足为F．
（1）求证：OF＝EC；
（2）若∠A＝30°，BD＝2，求AD的长．

【解答】（1）证明：连接OE，
∵AC是⊙O的切线，
∴OE⊥AC，
∴∠OEC＝90°，
∵OF⊥BC，
∴∠OFC＝90°，
∴∠OFC＝∠C＝∠OEC＝90°，
∴四边形OECF是矩形，
∴OF＝EC；
（2）解：∵BD＝2，
∴OE＝1，
∵∠A＝30°，OE⊥AC，
∴AO＝2OE＝2，
∴AD＝AO﹣OD＝2﹣1＝1．
二十．切线的性质（共1小题）
23．（2022•绍兴）如图，半径为6的⊙O与Rt△ABC的边AB相切于点A，交边BC于点C，D，∠B＝90°，连结OD，AD．
（1）若∠ACB＝20°，求的长（结果保留π）．
（2）求证：AD平分∠BDO．

【解答】（1）解：连结OA，如图：

∵∠ACB＝20°，
∴∠AOD＝40°，
∴＝＝；
（2）证明：∵OA＝OD，
∴∠OAD＝∠ODA，
∵AB切⊙O于点A，
∴OA⊥AB，
∵∠B＝90°，
∴OA∥BC，
∴∠OAD＝∠ADB，
∴∠ADB＝∠ODA，
∴AD平分∠BDO．
二十一．圆的综合题（共1小题）
24．（2022•台州）如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC交于点D，连接AD．
（1）求证：BD＝CD．
（2）若⊙O与AC相切，求∠B的度数．
（3）用无刻度的直尺和圆规作出劣弧的中点E．（不写作法，保留作图痕迹）

【解答】（1）证明：∵AB是直径，
∴∠ADB＝90°，
∴AD⊥BC，
∵AB＝AC，
∴BD＝CD；
（2）解：∵⊙O与AC相切，AB为直径，
∴BA⊥AC，
∵AB＝AC，
∴△BAC是等腰直角三角形，
∴∠B＝45°；
（3）解：如图，

作∠ABC的角平分线交于点E，则点E即是劣弧的中点．
二十二．作图—复杂作图（共2小题）
25．（2022•宁波）图1，图2都是由边长为1的小等边三角形构成的网格，每个小等边三角形的顶点称为格点，线段AB的端点均在格点上，分别按要求画出图形．
（1）在图1中画出等腰三角形ABC，且点C在格点上．（画出一个即可）
（2）在图2中画出以AB为边的菱形ABDE，且点D，E均在格点上．


【解答】解：（1）答案不唯一．

（2）
26．（2022•丽水）如图，在6×6的方格纸中，点A，B，C均在格点上，试按要求画出相应格点图形．

（1）如图1，作一条线段，使它是AB向右平移一格后的图形；
（2）如图2，作一个轴对称图形，使AB和AC是它的两条边；
（3）如图3，作一个与△ABC相似的三角形，相似比不等于1．

【解答】解：（1）如图1，CD为所作；
（2）如图2，
（3）如图3，△EDC为所作．

二十三．作图-旋转变换（共1小题）
27．（2022•温州）如图，在2×6的方格纸中，已知格点P，请按要求画格点图形（顶点均在格点上）．
（1）在图1中画一个锐角三角形，使P为其中一边的中点，再画出该三角形向右平移2个单位后的图形．
（2）在图2中画一个以P为一个顶点的钝角三角形，使三边长都不相等，再画出该三角形绕点P旋转180°后的图形．

【解答】解：（1）如图1中△ABC即为所求（答案不唯一）；
（2）如图2中△ABC即为所求（答案不唯一）．

二十四．锐角三角函数的定义（共1小题）
28．（2022•湖州）如图，已知在Rt△ABC中，∠C＝Rt∠，AB＝5，BC＝3．求AC的长和sinA的值．

【解答】解：∵∠C＝Rt∠，AB＝5，BC＝3，
∴AC＝＝＝4，
sinA＝＝．
答：AC的长为4，sinA的值为．
二十五．特殊角的三角函数值（共1小题）
29．（2022•金华）计算：（﹣2022）0﹣2tan45°+|﹣2|+．
【解答】解：原式＝1﹣2×1+2+3
＝1﹣2+2+3
＝4．
二十六．解直角三角形的应用（共1小题）
30．（2022•绍兴）圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．图2是一个根据某市地理位置设计的圭表平面示意图，表AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37°，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．

（1）求∠BAD的度数．
（2）求表AC的长（最后结果精确到0.1米）．
（参考数据：sin37°≈，cos37°≈，tan37°≈，tan84°≈）
【解答】解：（1）∵∠ADC＝84°，∠ABC＝37°，
∴∠BAD＝∠ADC﹣∠ABC＝47°，
答：∠BAD的度数是47°．
（2）在Rt△ABC中，，
∴．
在Rt△ADC中，，
∵BD＝4，
∴，
∴，
∴AC≈3.3（米），
答：表AC的长是3.3米．
二十七．解直角三角形的应用-坡度坡角问题（共1小题）
31．（2022•台州）如图1，梯子斜靠在竖直的墙上，其示意图如图2．梯子与地面所成的角α为75°，梯子AB长3m，求梯子顶部离地竖直高度BC．（结果精确到0.1m；参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）

【解答】解：在Rt△ABC中，AB＝3m，∠BAC＝75°，
sin∠BAC＝sin75°＝≈0.97，
解得BC≈2.9．
答：求梯子顶部离地竖直高度BC约为2.9m．
二十八．频数（率）分布表（共1小题）
32．（2022•温州）为了解某校400名学生在校午餐所需的时间，抽查了20名学生在校午餐所花的时间，由图示分组信息得：A，C，B，B，C，C，C，A，B，C，C，C，D，B，C，C，C，E，C，C．
分组信息
A组：5＜x≤10
B组：10＜x≤15
C组：15＜x≤20
D组：20＜x≤25
E组：25＜x≤30
注：x（分钟）为午餐时间！
某校被抽查的20名学生在校午餐所花时间的频数表
组别
划记
频数
A

2
B

4
C
　　
　12　
D
　　
　1　
E
　　
　1　
合计
20
（1）请填写频数表，并估计这400名学生午餐所花时间在C组的人数．
（2）在既考虑学生午餐用时需求，又考虑食堂运行效率的情况下，校方准备在15分钟，20分钟，25分钟，30分钟中选择一个作为午餐时间，你认为应选择几分钟为宜？说明理由．



【解答】解：（1）频数表填写如图，

＝240（名）．
答：这400名学生午餐所花时间在C组的有240名．
（2）①选择25分钟，有19人能按时完成用餐，占比95%，可以鼓励最后一位同学适当加快用餐速度，有利于食堂提高运行效率，
②选择20分钟，有18人能按时完成用餐，占比 90%，可以鼓励最后两位同学适当加快用餐速度或采用合理照顾如优先用餐等方式，以满足学生午餐用时需求，又提高食堂的运行效率．
③选择30分钟，能说明所有学生都能完成用餐，但未考虑食堂的运行效率．
二十九．扇形统计图（共3小题）
33．（2022•绍兴）双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长x（单位：小时）的情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．
八年级学生每日完成书面作业所需时长情况的统计表
组别
所需时长（小时）
学生人数（人）
A
0＜x≤0.5
15
B
0.5＜x≤1
m
C
1＜x≤1.5
n
D
1.5＜x≤2
5
（1）求统计表中m，n的值．
（2）已知该校八年级学生有800人，试估计该校八年级学生中每日完成书面作业所需时长满足0.5＜x≤1.5的共有多少人．

【解答】解：（1）被调查总人数：15÷15%＝100（人），
∴m＝100×60%＝60（人），
n＝100﹣15﹣60﹣5＝20（人），
答：m为60，n为20；
（2）∵当0.5＜x≤1.5时，在被调查的100人中有60+20＝80（人），
∴在该校八年级学生800人中，每日完成书面作业所需时长满足0.5＜x≤1.5的共有800×＝640（人），
答：估计共有640人．
34．（2022•台州）某中学为加强学生的劳动教育，需要制定学生每周劳动时间（单位：小时）的合格标准，为此随机调查了100名学生目前每周劳动时间，获得数据并整理成下表．
学生目前每周劳动时间统计表
每周劳动时间x（小时）
0.5≤x＜1.5
1.5≤x＜2.5
2.5≤x＜3.5
3.5≤x＜4.5
4.5≤x＜5.5
组中值
1
2
3
4
5
人数（人）
21
30
19
18
12
（1）画扇形图描述数据时，1.5≤x＜2.5这组数据对应的扇形圆心角是多少度？
（2）估计该校学生目前每周劳动时间的平均数．
（3）请你为该校制定一个学生每周劳动时间的合格标准（时间取整数小时），并用统计量说明其合理性．
【解答】解：（1）×100%＝30%，
360°×30%＝108°；
（2）＝＝2.7（小时），
答：由样本估计总体可知，该校学生目前每周劳动时间的平均数约为2.7小时．
（3）（以下两种方案选一即可）
①从平均数看，标准可以定为3小时，
理由：平均数为2.7小时，说明该校学生目前每周劳动时间平均水平为2.7小时，把标准定为3小时，至少有30%的学生目前每周劳动时间能达标，同时至少还有51%的学生未达标，这样使多数学生有更高的努力目标．
②从中位数的范围或频数看，标准可以定位2小时，
理由：该校学生目前每周劳动时间的中位数在1.5≤x＜2.5范围内，把标准定为2小时，至少有49%的学生目前能达标，同时至少有21%的学生未达标，这样有利于学生建立达标的信心，促进未达标学生努力达标，提高该校学生的劳动积极性．
35．（2022•金华）学校举办演讲比赛，总评成绩由“内容、表达、风度、印象”四部分组成．九（1）班组织选拔赛，制定的各部分所占比例如图，三位同学的成绩如下表．请解答下列问题：
三位同学的成绩统计表

内容
表达
风度
印象
总评成绩
小明
8
7
8
8
m
小亮
7
8
8
9
7.85
小田
7
9
7
7
7.8
（1）求图中表示“内容”的扇形的圆心角度数．
（2）求表中m的值，并根据总评成绩确定三人的排名顺序．
（3）学校要求“内容”比“表达”重要，该统计图中各部分所占比例是否合理？如果不合理，如何调整？

【解答】解：（1）设“内容”所占比例为x，“风度”所占比例为y，由题意得：
，
整理得：，
解得：，
∴“内容”所占比例为30%，“风度”所占比例为15%，
∴表示“内容”的扇形的圆心角度数为360°×30%＝108°；

（2）m＝8×30%+7×40%+8×15%+8×15%＝7.6．
∵7.85＞7.8＞7.6，
三人成绩从高到低的排名顺序为：小亮，小田，小明；

（3）班级制定的各部分所占比例不合理．
可调整为：“内容”所占百分比为40%，“表达”所占百分比为30%，其它不变（答案不唯一）．
三十．条形统计图（共3小题）
36．（2022•舟山）某教育部门为了解本地区中小学生参加家庭劳动时间的情况，随机抽取该地区1200名中小学生进行问卷调查，并将调查问卷（部分）和结果描述如下：
调查问卷（部分）
1．你每周参加家庭劳动时间大约是______h．
如果你每周参加家庭劳动时间不足2h，请回答第2个问题：
2．影响你每周参加家庭劳动的主要原因是______（单选）．
A．没时间
B．家长不舍得
C．不喜欢
D．其它

中小学生每周参加家庭劳动时间x（h） 分为5组：第一组（0≤x＜0.5），第二组（0.5≤x＜1），第三组（1≤x＜1.5），第四组（1.5≤x＜2），第五组（x≥2）．
根据以上信息，解答下列问题：
（1）本次调查中，中小学生每周参加家庭劳动时间的中位数落在哪一组？
（2）在本次被调查的中小学生中，选择“不喜欢”的人数为多少？
（3）该教育部门倡议本地区中小学生每周参加家庭劳动时间不少于2h．请结合上述统计图，对该地区中小学生每周参加家庭劳动时间的情况作出评价，并提出两条合理化建议．
【解答】解：（1）由统计图可知，抽取的这1200名学生每周参加家庭劳动时间的中位数为第600个和第601个数据的平均数，
故中位数落在第二组；
（2）（1200﹣200）×（1﹣8.7%﹣43.2%﹣30.6%）＝175（人），
答：在本次被调查的中小学生中，选择“不喜欢”的人数为175人；
（3）由统计图可知，该地区中小学生每周参加家庭劳动时间大多数都小于2h，建议学校多开展劳动教育，养成劳动的好习惯．（答案不唯一）．
37．（2022•湖州）为落实“双减”政策，切实减轻学生学业负担，丰富学生课余生活，某校积极开展“五育并举”课外兴趣小组活动，计划成立“爱心传递”、“音乐舞蹈”、“体育运动”、“美工制作”和“劳动体验”五个兴趣小组，要求每位学生都只选其中一个小组．为此，随机抽查了本校各年级部分学生选择兴趣小组的意向，并将抽查结果绘制成如下统计图（不完整）．

根据统计图中的信息，解答下列问题：
（1）求本次被抽查学生的总人数和扇形统计图中表示“美工制作”的扇形的圆心角度数；
（2）将条形统计图补充完整；
（3）该校共有1600名学生，根据抽查结果，试估计全校选择“爱心传递”兴趣小组的学生人数．

【解答】解：（1）本次被抽查学生的总人数是60÷30%＝200（人），
扇形统计图中表示“美工制作”的扇形的圆心角度数是＝36°；
（2）“音乐舞蹈”的人数为200﹣50﹣60﹣20﹣40＝30（人），
补全条形统计图如下：

（3）估计全校选择“爱心传递”兴趣小组的学生人数为＝400（人）．
38．（2022•丽水）某校为了解学生在“五•一”小长假期间参与家务劳动的时间t（小时），随机抽取了本校部分学生进行问卷调查．要求抽取的学生在A，B，C，D，E五个选项中选且只选一项，并将抽查结果绘制成如下两幅不完整的统计图，请根据图中信息回答问题：

（1）求所抽取的学生总人数；
（2）若该校共有学生1200人，请估算该校学生参与家务劳动的时间满足3≤t＜4的人数；
（3）请你根据调查结果，对该校学生参与家务劳动时间的现状作简短评述．
【解答】解：（1）18÷36%＝50（人），
故所抽取的学生总人数为50人；
（2）1200×＝240（人），
答：估算该校学生参与家务劳动的时间满足3≤t＜4的人数为240人；
（3）由题意可知，该校学生在“五•一”小长假期间参与家务劳动时间在1≤t＜2占最多数，中位数位于2≤t＜3这一组（答案不唯一）．
三十一．折线统计图（共1小题）
39．（2022•宁波）小聪、小明参加了100米跑的5期集训，每期集训结束时进行测试．根据他们集训时间、测试成绩绘制成如下两个统计图．

根据图中信息，解答下列问题：
（1）这5期的集训共有多少天？
（2）哪一期小聪的成绩比他上一期的成绩进步最多？进步了多少秒？
（3）根据统计数据，结合体育运动的实际，从集训时间和测试成绩这两方面，简要说说你的想法．
【解答】解：（1）4+7+10+14+20＝55（天）．
答：这5期的集训共有55天．
（2）11.72﹣11.52＝0.2（秒）．
答：第3期小聪的成绩比他上一期的成绩进步最多，进步了0.2秒．
（3）个人测试成绩与很多因素有关，如集训时间不是越长越好，集训时间过长，可能会造成劳累，导致成绩下降；集训的时间为10天或14天时成绩最好．