数学九年级上册25.2 用列举法求概率精品ppt课件

这是一份数学九年级上册25.2 用列举法求概率精品ppt课件，文件包含2521《用列举法求概率》课件pptx、2521《用列举法求概率》练习doc、2521《用列举法求概率》教案doc等3份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

25.2.1 用列举法求概率
目录
情景导入
　　回答下列问题，并说明理由．（1）掷一枚硬币，正面向上的概率是_______；（2）袋子中装有 5 个红球，3 个绿球，这些球除了 颜色外都相同，从袋子中随机摸出一个球，它是红 色的概率为________； （3）掷一个骰子，观察向上一面的点数，点数大 于 4 的概率为______．
情景导入
　　在一次试验中，如果可能出现的结果只有有限个，且各种结果出现的可能性大小相等，那么我们可以通过列举试验结果的方法，求出随机事件发生的概率，这种求概率的方法叫列举法．
新知探究1
　　例1　同时向空中抛掷两枚质地均匀的硬币，求下 列事件的概率：　　（1）两枚硬币全部正面向上； 　　（2）两枚硬币全部反面向上；　　（3）一枚硬币正面向上、一枚硬币反面向上．
新知探究1
　　方法一：将两枚硬币分别记做 A、B，于是可以直接列举得到：（A正，B正），（A正，B反）， （A反，B正）， （A反，B反）四种等可能的结果．故：
新知探究1
方法二：将同时掷两枚硬币，想象为先掷一枚，再掷一枚，分步思考：在第一枚为正面的情况下第二枚硬币有正、反两种情况，同理第一枚为反面的情况下第二枚硬币有正、反两种情况．
新知探究1
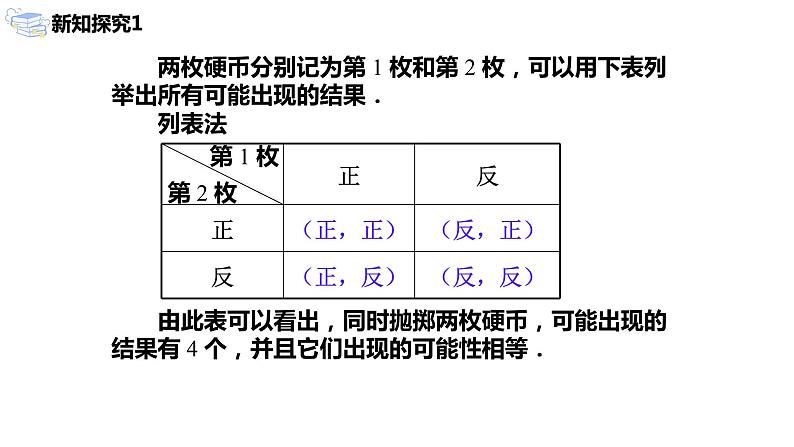
　　两枚硬币分别记为第 1 枚和第 2 枚，可以用下表列举出所有可能出现的结果．
第 1 枚
第 2 枚
由此表可以看出，同时抛掷两枚硬币，可能出现的结果有 4 个，并且它们出现的可能性相等．
　　列表法
新知探究1
　　例2　同时掷两枚质地均匀的骰子，计算下列事件的概率：　　（1）两枚骰子的点数相同；　　（2）两枚骰子点数的和是 9；　　（3）至少有一枚骰子的点数为 2．
新知探究1
　　解：两枚骰子分别记为第 1 枚和第 2 枚，可以用下表列举出所有可能的结果．
第1枚
第2枚
　　可以看出，同时掷两枚骰子，可能出现的结果有 36种，并且它们出现的可能性相等．
新知探究1
第1枚
第2枚
　　（1）两枚骰子点数相同（记为事件 A）的结果有 6种，即（1，1），（2，2），（3，3），（4，4）， （5，5），（6，6），所以，P（A）=　 =　．
新知探究1
第1枚
第2枚
　　（2）两枚骰子点数之和是 9（记为事件 B）的结果有 4 种，即（3，6），（4，5），（5，4），（6，3），所以， P（B）=　 =　．
新知探究1
第1枚
第2枚
　　（3）至少有一枚骰子的点数是 2（记为事件 C）的结果有 11 种，所以， P（C）= ．
课堂练习1
1. 不透明袋子中装有1个红球，2个绿球，除颜色外无其他差别。随机摸出一个小球后， ，再随机摸出一个。请补全表格，并求出第一次摸到红球，第二次摸到绿球的概率。
解：如右表。
总的结果数有9种，符合题意的有2种
 
(红,红)
(绿1,红)
(绿2,红)
(红,绿1)
(红,绿2)
(绿1,绿1)
(绿1,绿2)
(绿2,绿1)
(绿2,绿2)
放回并摇匀
课堂小结
这节课有哪些收获？
课堂小结
列举法
关键
常用方法
直接列举法
列表法
适用对象
两个试验因素或分两步进行的试验
基本步骤
列表；确定m、n值代入概率公式计算
在于正确列举出试验结果的各种可能性.
确保试验中每种结果出现的可能性大小相等
前提条件
课堂检测
1. 不透明袋子中装有1个红球，2个绿球，除颜色外无其他差别。随机摸出一个小球后， ，再随机摸出一个。求第一次摸到红球，第二次摸到绿球的概率。
解：如右表。
总的结果数有6种，符合题意的有2种
 
不放回
课堂检测
2.某班级准备召开主题班会，现从由3名男生和1名女生所组成的班委中，随机选取两人担任主持人，求两名主持人恰为一男一女的概率。
解：如右表。总的结果数有12种，符合题意的有6种
 
谢谢观看