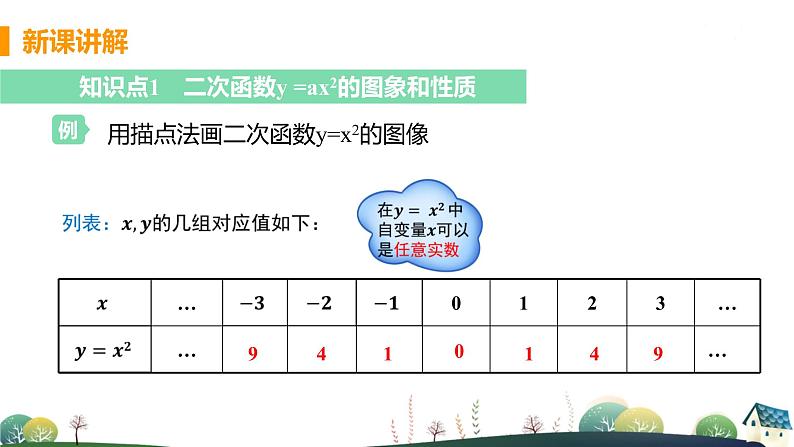
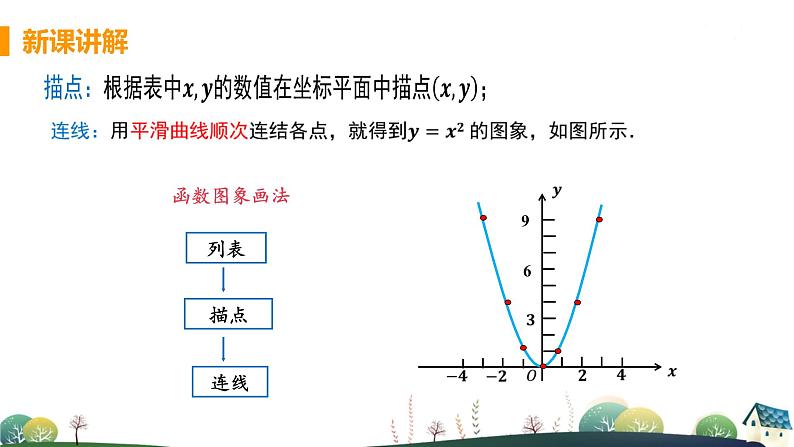
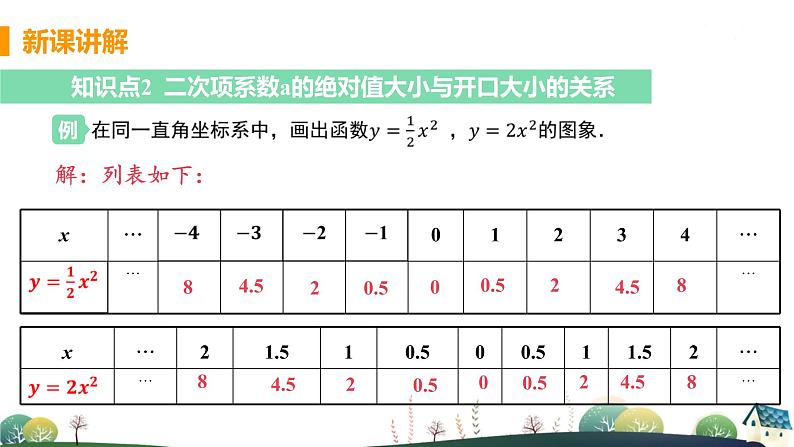
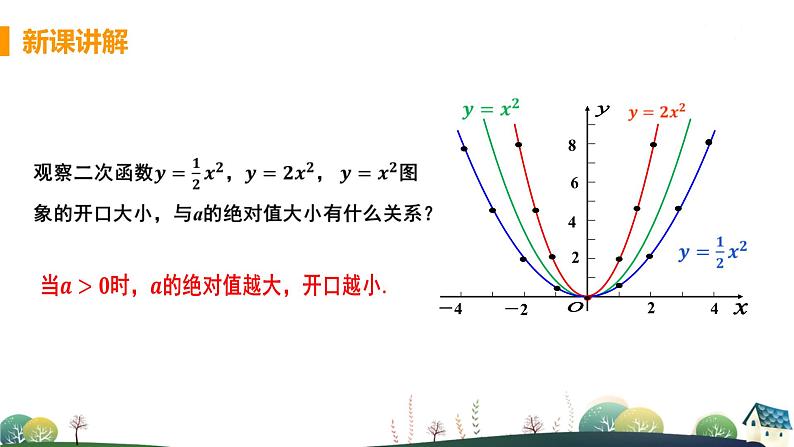
初中数学浙教版九年级上册1.2 二次函数的图象课文内容课件ppt

1.2 二次函数的图象

一、选择题（本题包括7小题.每小题只有1个选项符合题意）

1．    若二次函数y=ax2的图象经过点P（-2，4），则该图象必经过点（    ）

A．（2，4）          B．（-2，-4）        C．（-4，2）       D．（4，-2）

2．    二次函数y=-x2+bx+c的图象如图，若点A（x1，y1），B（x2，y2）在此函数图象上，x1<x2<1，则y1与y2的大小关系是（    ）

（第2题图）

A．y1≤y2           B．y1<y2            C．y1≥y2           D．y1>y2

3．    若二次函数y=ax2+bx-1（a≠0）的图象经过点（1，1），则a+b+1的值是（    ）

A．-3               B．-1                C．2               D．3

4．    已知二次函数y=a（x-2）2+c，若当x=x1时，函数值为y1；当x=x2时，函数值为y2，若|x1-2|>|x2-2|，则下列表达式正确的是（    ）

A．y1+y2>0           B．y1-y2>0            C．a（y1-y2）>0   D．a（y1+y2）>0

5．    要将抛物线y=x2+2x+3平移后得到抛物线y=x2，下列平移方法正确的是（    ）

A．向左平移1个单位长度，再向上平移2个单位长度

B．向左平移1个单位长度，再向下平移2个单位长度

C．向右平移1个单位长度，再向上平移2个单位长度

D．向右平移1个单位长度，再向下平移2个单位长度

6．    对于实数a，b，定义一种运算“⊗”为：a⊗b=a2+ab-2，有下列命题：

①1⊗3=2；②方程x⊗1=0的根为x1=-2，x2=1；③不等式组的解集为-1<x<4；

④点（，）在函数y=x⊗（-1）的图象上．

其中正确的是（    ）

A．①②③④         B．①③             C．①②③         D．③④

7．    二次函数y=ax2+bx+c（a≠0）的图象如图，若M=a+b-c，N=4a-2b+c，P=2a-b．则M，N，P中，值小于0的数有（    ）

（第7题图）

A．3个                 B．2个              C．1个            D．0个

二、填空题 （本题包括4小题）

8．    抛物线y=ax2+bx+2经过点（-2，3），则3b-6a=　　．

9．    当x=m和x=n（m≠n）时，二次函数y=x2-2x+3的函数值相等，当x=m+n时，函数y=x2-2x+3的值为　　．

10．如图，在平面直角坐标系中，点A在抛物线y=x2-2x+2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连结BD，则对角线BD的最小值为　　．

（第10题图）

11．在直角坐标系xOy中，对于点P（x，y）和Q（x，y′），给出如下定义：若y′=，则称点Q为点P的“可控变点”．

例如：点（1，2）的“可控变点”为点（1，2），点（-1，3）的“可控变点”为点（-1，-3）．

（1）若点（-1，-2）是一次函数y=x+3图象上点M的“可控变点”，则点M的坐标为　　．

（2）若点P在函数y=-x2+16（-5≤x≤a）的图象上，其“可控变点”Q的纵坐标y′的取值范围是-16<y′≤16，则实数a的取值范围是　　．

三、解答题 （本题包括4小题）

12. 已知抛物线y＝ax2+bx﹣3（a≠0）经过点（﹣1，0）和（3，0）．

（1）求a，b的值．

（2）求抛物线向左平移2个单位后的函数解析式．

13. 画出函数y＝x2+4x+3的图象，并指出函数图象的特征．

14. 如图，点A在y轴正半轴，点B，C在二次函数y＝x2的图象上，四边形OBAC是菱形，∠OBA＝120°，求点B的坐标以及菱形OBAC的面积．

（第14题图）

15.在平面直角坐标系xOy中，抛物线C：y＝ax2﹣2ax+3与直线l：y＝kx+b交于A，B两点，且点A在y轴上，点B在x轴的正半轴上．

（1）求点A的坐标；

（2）若a＝﹣1，求直线l的解析式；

（3）若﹣3＜k＜﹣1，求a的取值范围．

（第15题图）

1.2 二次函数的图象

参考答案

一、1． A   2．B   3．D   4.C   5．D   6．C   7． A

二、8.    9.3   20．y3>y1>y2    10．1   11.（-1，2）；0≤a<4

三、12. 解：（1）设抛物线解析式为y＝a（x+1）（x﹣3），

即y＝ax2﹣2ax﹣3a，

所以﹣3a＝﹣3，解得a＝1，

所以抛物线解析式为y＝x2﹣2x﹣3；

（2）y＝（x﹣1）2﹣4，

抛物线的顶点坐标为（1，﹣4），把（1，﹣4）向左平移2个单位后所得对应点的坐标为（﹣1，﹣4），所以平移后的抛物线解析式为y＝（x+1）2﹣4．

13. 解：列表：

函数y＝x2+4x+3的图象如下：

（第13题答图）

图象特征有：①为一条开口向上的抛物线；②与x轴交点坐标为（﹣3，0）和（﹣1，0），与y轴交点坐标为（0，3）；③为轴对称图形，对称轴为直线x＝﹣2；④抛物线有最低点（﹣2，﹣1）即函数在x＝﹣2时，有最小值为﹣1；⑤当x＜﹣2时，抛物线从左到右下降，即y随x的增大而减小，当x＞﹣2时，抛物线从左到右上升，即y随x的增大而增大．

14. 解：连接BC交OA于P，如图，

∵四边形OBAC是菱形，∠OBA＝120°，

∴∠BOC＝60°，BC⊥OA，PA＝OP，PC＝PB，

∴∠BOP＝∠BOC＝30°，

设B（t，t2），

在Rt△OBP中，OP＝BP，

∴t2＝t，解得t1＝0（舍去），t2＝1，

∴B（1，），

∵BC＝2，OA＝2，

∴菱形OBAC的面积＝×2×2＝2．

（第14题答图）

15.解：（1）∵抛物线C：y＝ax2﹣2ax+3与y轴交于点A，

∴点A的坐标为（0，3）．

（2）当a＝﹣1时，抛物线C为y＝﹣x2+2x+3．

∵抛物线C与x轴交于点B，且点B在x轴的正半轴上，

∴点B的坐标为（3，0）．

∵直线l：y＝kx+b过A，B两点，

∴解得

∴直线l的解析式为y＝﹣x+3．

（3）如图，

当a＞0时，

当a＝3时，抛物线C过点B（1，0），此时k＝﹣3．

结合函数图象可得a＞3．

当a＜0时，

当a＝﹣1时，抛物线C过点B（3，0），此时k＝﹣1．

结合函数图象可得a＜﹣1．

综上所述，a的取值范围是a＜﹣1或a＞3．

（第15题答图）