2022年山东省泰安市东平县中考数学一模试卷

这是一份2022年山东省泰安市东平县中考数学一模试卷，共30页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022年山东省泰安市东平县中考数学一模试卷
一、选择题（本大题共12个小题，每小题4分，共48分.每小题给出的四个答案中，只有一项是正确的.）
1．（4分）在0，2，﹣2，﹣3.5这四个数中，是负整数的是（　　）
A．0 B．2 C．﹣2 D．﹣3.5
2．（4分）下列计算结果正确的是（　　）
A．（a3）4＝a12 B．a3•a3＝a9
C．（﹣2a）2＝﹣4a2 D．（ab）2＝ab2
3．（4分）如图是某个几何体的三视图，该几何体是（　　）

A．长方体 B．正方体 C．三棱柱 D．圆柱
4．（4分）如图，已知直线AC∥BD，BF与AC交于点F，若∠A＝23°，∠AEB＝58°，则∠B＝（　　）

A．23° B．58° C．35° D．45°
5．（4分）八年级（1）班30名学生的身高情况如表：
身高（m）
1.45
1.48
1.50
1.53
1.55
1.65
1.70
人数
x
y
6
8
5
3
1
关于身高的统计量中，不随x、y的变化而变化的有（　　）
A．众数，中位数 B．中位数，方差
C．平均数，方差 D．平均数，众数
6．（4分）如图，AB是⊙O的直径，点P是⊙O外一点，PO交⊙O于点C，连接BC，PA．若∠P＝36°，且PA与⊙O相切，则此时∠B等于（　　）

A．27° B．32° C．36° D．54°
7．（4分）关于x的一元二次方程（k﹣1）x2+4x+k﹣1＝0有两个相等的实数根，则k的值为（　　）
A．1 B．﹣1 C．3或﹣1 D．﹣3
8．（4分）抛物线y＝x2+1经过平移得到抛物线y＝（x﹣6）2+4，平移过程正确的是（　　）
A．先向左平移6个单位，再向上平移3个单位
B．先向左平移6个单位，再向下平移3个单位
C．先向右平移6个单位，再向上平移3个单位
D．先向右平移6个单位，再向下平移3个单位
9．（4分）如图，四边形ABCD是⊙O的内接四边形，若∠C＝100°，则∠BOD的度数是（　　）

A．100° B．120° C．130° D．160°
10．（4分）如图，将▱DEBF的对角线EF向两端延长，分别至点A和点C，且使AE＝CF，连接AB，BC，AD，CD．求证：四边形ABCD为平行四边形．以下是证明过程，其顺序已被打乱，①∴四边形ABCD为平行四边形；②∵四边形DEBF为平行四边形，∴OD＝OB，OE＝OF；③连接BD，交AC于点O；④又∵AE＝CF，∴AE+OE＝CF+OF，即OA＝OC．正确的证明步骤是（　　）

A．①②③④ B．③④②① C．③②④① D．④③②①
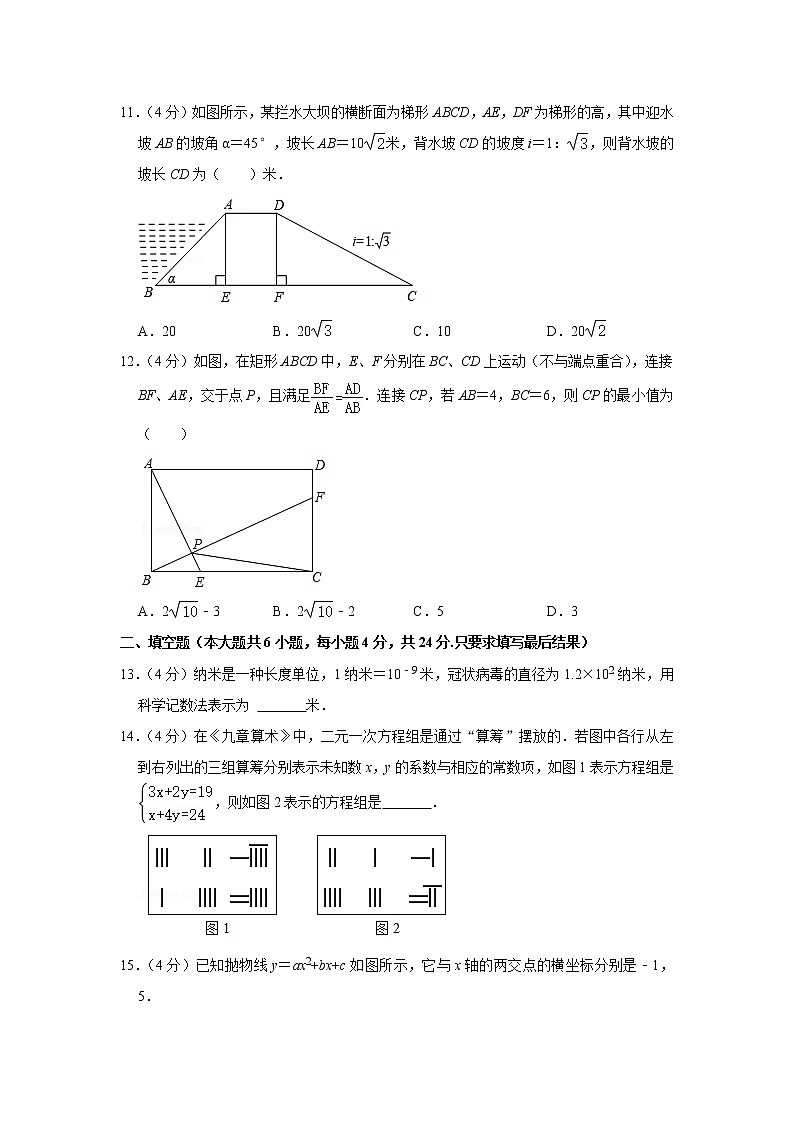
11．（4分）如图所示，某拦水大坝的横断面为梯形ABCD，AE，DF为梯形的高，其中迎水坡AB的坡角α＝45°，坡长AB＝10米，背水坡CD的坡度i＝1：，则背水坡的坡长CD为（　　）米．

A．20 B．20 C．10 D．20
12．（4分）如图，在矩形ABCD中，E、F分别在BC、CD上运动（不与端点重合），连接BF、AE，交于点P，且满足．连接CP，若AB＝4，BC＝6，则CP的最小值为（　　）

A．2﹣3 B．2﹣2 C．5 D．3
二、填空题（本大题共6小题，每小题4分，共24分.只要求填写最后结果）
13．（4分）纳米是一种长度单位，1纳米＝10﹣9米，冠状病毒的直径为1.2×102纳米，用科学记数法表示为 　 　米．
14．（4分）在《九章算术》中，二元一次方程组是通过“算筹”摆放的．若图中各行从左到右列出的三组算筹分别表示未知数x，y的系数与相应的常数项，如图1表示方程组是，则如图2表示的方程组是　 　．

15．（4分）已知抛物线y＝ax2+bx+c如图所示，它与x轴的两交点的横坐标分别是﹣1，5．
对于下列结论：
①abc＞0；
②方程ax2+bx+c＝0的根是x1＝﹣1，x2＝5；
③9a﹣3b+c＜0；
④当x＜2时，y随着x的增大而增大．
其中正确的结论是 　 　（填写结论的序号）．

16．（4分）如图，在Rt△ABC中，∠C＝90°，分别以AB、BC、AC边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”．当AB＝8，BC＝4时，则阴影部分的面积为 　 　．

17．（4分）如图，在平面直角坐标系中，点A，B，C的坐标分别为（8，0），（8，6），（0，6），点D为线段BC上一动点，将△OCD沿OD翻折，使点C落到点E处．当B，E两点之间距离最短时，点D的坐标为 　 　．

18．（4分）如图，已知等边△ABC，D是边BC的中点，过D作DE∥AB于E，连接BE交AD于D1；过D1作D1E1∥AB于E1，连接BE1交AD于D2；过D2作D2E2∥AB于E2，…，如此继续，若记S△BDE为S1，记为S2，记为S3…，若S△ABC面积为Scm2，则Sn＝　 　cm2（用含n与S的代数式表示）

三、解答题（本大题共7小题，共78分写出必要的文字说明、证明过程或推演步骤）
19．（10分）（1）先化简，再求值：（x﹣1﹣）÷，其中x＝﹣2．
（2）解不等式：﹣≤1．
20．（10分）“青年大学习”是由共青团中央发起，广大青年参与，通过学习来提升自身理论水平、思维层次的行动．梦想从学习开始，事业从实践起步．某校为了解九年级学生学习“青年大学习”的情况，随机抽取部分九年级学生进行了问卷调查，按照调查结果，将学习情况分为优秀、良好、合格、较差四个等级．学校绘制了如下不完整的统计图，根据图中信息解答下列问题：

（1）本次参与问卷调查的初中生共有　 　人，将条形统计图补充完整；
（2）扇形统计图中“合格”所对应的百分比为　 　%，“较差”所对应的圆心角度数为　 　度；
（3）该校某班有4名同学（2名男同学、2名女同学）在调查中获得“优秀”等级，班主任将从这4名同学中随机选取2名同学，代表班级参加学校组织的“青年大学习”演讲大赛，请用列表或画树状图的方法，求所选两位同学恰好是1名男同学和1名女同学的概率．
21．（11分）如图，一次函数y＝x+1的图象与x轴交于点A，与y轴交于点C，与反比例函数y＝（k≠0）的图象交于B，D两点，且AC＝BC．
（1）求反比例函数的解析式；
（2）已知P是x轴正半轴上一点，作PM⊥x轴交直线AB于点M，交双曲线于点N，当O，C，M，N为顶点的四边形为平行四边形时，请写出点P的坐标．

22．（11分）我校在开学初购买了A、B两种品牌的排球，购买A品牌排球花费了2500元，购买B品牌排球花费了2000元，且购买A品牌的排球数量是购买B品牌排球数量的2倍，已知购买一个B品牌排球比购买一个A品牌排球多花30元．
（1）求购买一个A品牌、一个B品牌的排球各需多少元？
（2）学校决定再次购进A、B两种品牌排球共50个，恰逢两种品牌排球的售价进行调整，A品牌排球售价比第一次购买时提高了8%，B品牌排球按第一次购买时售价的9折出售，如果学校第二次购买A、B两种品牌排球的总费用不超过3240元，那么学校第二次最多可购买多少个B品牌排球？
23．（12分）在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．
（1）如图1所示，点M，N分别在线段AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝时，求线段AM的长；
（2）如图2所示，点E，F分别在AB，AC上，且BE＝AF，求证：△DEF是等腰直角三角形；
（3）如图3所示，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+AN＝AM．
24．（12分）已知抛物线y＝ax2+bx+c（a≠0）经过A（4，0）、B（﹣1，0）、C（0，4）三点．

（1）求抛物线的函数解析式；
（2）如图1，点D是在直线AC上方的抛物线的一点，DN⊥AC于点N，DM∥y轴交AC于点M，求△DMN周长的最大值及此时点D的坐标；
（3）如图2，点P为第一象限内的抛物线上的一个动点，连接OP，OP与AC相交于点Q，求的最大值．
25．（12分）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且CF是⊙O的切线．
（1）求证：∠DCF＝∠CAD．
（2）探究线段CF，FD，FA的数量关系并说明理由；
（3）若cosB＝，AD＝2，求FD的长．


2022年山东省泰安市东平县中考数学一模试卷
参考答案与试题解析
一、选择题（本大题共12个小题，每小题4分，共48分.每小题给出的四个答案中，只有一项是正确的.）
1．（4分）在0，2，﹣2，﹣3.5这四个数中，是负整数的是（　　）
A．0 B．2 C．﹣2 D．﹣3.5
【解答】解：A．0既不是正数，也不是负数，故本选项不合题意；
B．2是正整数，故本选项不合题意；
C．﹣2是负整数，故本选项符合题意；
D．﹣3.5不是整数，故本选项不合题意．
故选：C．
2．（4分）下列计算结果正确的是（　　）
A．（a3）4＝a12 B．a3•a3＝a9
C．（﹣2a）2＝﹣4a2 D．（ab）2＝ab2
【解答】解：A、原式＝a12，故A符合题意．
B、原式＝a6，故B不符合题意．
C、原式＝4a2，故C不符合题意．
D、原式＝a2b2，故D不符合题意．
故选：A．
3．（4分）如图是某个几何体的三视图，该几何体是（　　）

A．长方体 B．正方体 C．三棱柱 D．圆柱
【解答】解：俯视图是三角形的，因此这个几何体的上面、下面是三角形的，正视图和左视图是长方形的，且左视图的长方形的宽较窄，因此判断这个几何体是三棱柱，
故选：C．
4．（4分）如图，已知直线AC∥BD，BF与AC交于点F，若∠A＝23°，∠AEB＝58°，则∠B＝（　　）

A．23° B．58° C．35° D．45°
【解答】解：∵∠AEB＝58°，
∴∠AEF＝180°﹣58°＝122°，
∴∠AFE＝180°﹣∠A﹣∠AEF＝180°﹣23°﹣122°＝35°，
∵AC∥BD，
∴∠B＝∠AFE＝35°．
故选：C．
5．（4分）八年级（1）班30名学生的身高情况如表：
身高（m）
1.45
1.48
1.50
1.53
1.55
1.65
1.70
人数
x
y
6
8
5
3
1
关于身高的统计量中，不随x、y的变化而变化的有（　　）
A．众数，中位数 B．中位数，方差
C．平均数，方差 D．平均数，众数
【解答】解：由题意得：x+y＝30﹣6﹣8﹣5﹣3﹣1＝7，
所以众数为1.53，中位数也是1.53，
所以众数、中位数不会随着x、y的变化而变化，
故选：A．
6．（4分）如图，AB是⊙O的直径，点P是⊙O外一点，PO交⊙O于点C，连接BC，PA．若∠P＝36°，且PA与⊙O相切，则此时∠B等于（　　）

A．27° B．32° C．36° D．54°
【解答】解：∵PA是⊙O的切线，
∴∠PAO＝90°，
∴∠AOP＝90°﹣∠P＝54°，
∵OB＝OC，
∴∠AOP＝2∠B，
∴∠B＝∠AOP＝27°，
故选：A．
7．（4分）关于x的一元二次方程（k﹣1）x2+4x+k﹣1＝0有两个相等的实数根，则k的值为（　　）
A．1 B．﹣1 C．3或﹣1 D．﹣3
【解答】解：∵关于x的一元二次方程（k﹣1）x2+4x+k﹣1＝0有两个相等的实数根，
∴k﹣1≠0且Δ＝42﹣4（k﹣1）2＝0，
解得k＝3或﹣1．
故选：C．
8．（4分）抛物线y＝x2+1经过平移得到抛物线y＝（x﹣6）2+4，平移过程正确的是（　　）
A．先向左平移6个单位，再向上平移3个单位
B．先向左平移6个单位，再向下平移3个单位
C．先向右平移6个单位，再向上平移3个单位
D．先向右平移6个单位，再向下平移3个单位
【解答】解：抛物线y＝x2+1的顶点坐标为（0，1），抛物线y＝x2的顶点坐标为（0，0），而点（0，1）先向右平移6个单位，再向上平移3个单位后可得点（6，4），
所以抛物线y＝x2+1先向右平移6个单位，再向上平移3个单位后可得抛物线y＝（x﹣6）2+4，
故选：C．
9．（4分）如图，四边形ABCD是⊙O的内接四边形，若∠C＝100°，则∠BOD的度数是（　　）

A．100° B．120° C．130° D．160°
【解答】解：∵四边形ABCD是⊙O的内接四边形，∠C＝100°，
∴∠A＝180°﹣∠C＝80°，
∴∠BOD＝2∠A＝160°，
故选：D．
10．（4分）如图，将▱DEBF的对角线EF向两端延长，分别至点A和点C，且使AE＝CF，连接AB，BC，AD，CD．求证：四边形ABCD为平行四边形．以下是证明过程，其顺序已被打乱，①∴四边形ABCD为平行四边形；②∵四边形DEBF为平行四边形，∴OD＝OB，OE＝OF；③连接BD，交AC于点O；④又∵AE＝CF，∴AE+OE＝CF+OF，即OA＝OC．正确的证明步骤是（　　）

A．①②③④ B．③④②① C．③②④① D．④③②①
【解答】解：连接BD，交AC于点O，如图所示：
∵四边形DEBF为平行四边形，
∴OD＝OB，OE＝OF，
又∵AE＝CF，
∴AE+OE＝CF+OF，
即OA＝OC，
∴四边形ABCD为平行四边形，
即正确的证明步骤是③②④①，
故选：C．

11．（4分）如图所示，某拦水大坝的横断面为梯形ABCD，AE，DF为梯形的高，其中迎水坡AB的坡角α＝45°，坡长AB＝10米，背水坡CD的坡度i＝1：，则背水坡的坡长CD为（　　）米．

A．20 B．20 C．10 D．20
【解答】解：由题意得：四边形AEFD是矩形，
∴DF＝AE，
∵迎水坡AB的坡角α＝45°，坡长AB＝10米，
∴DF＝AE＝10×sin45°＝10（米），
∵背水坡CD的坡度i＝1：，
∴tanC＝i＝＝＝，
∴∠C＝30°，
∴CD＝2DF＝2AE＝20（米），
故选：A．
12．（4分）如图，在矩形ABCD中，E、F分别在BC、CD上运动（不与端点重合），连接BF、AE，交于点P，且满足．连接CP，若AB＝4，BC＝6，则CP的最小值为（　　）

A．2﹣3 B．2﹣2 C．5 D．3
【解答】解：
∵四边形ABCD是矩形，
∴∠BAD＝∠ABC＝90°，
则∠BAE+∠BEP＝90°，
又∵，
∴
∴△ABE∽△BCF，
∴∠BAE＝∠CBF，
∴∠CBF+∠BEP＝90°，即AE⊥BF，
∴点P为以AB的中点O为圆心，AB为直径的圆上一点，

则当点O、P、C三点共线时，OC的值为最小值，即CP的值也为最小值．
∴当CP取最小值时，CP＝OC﹣OP，
∵AB＝4，BC＝6，∠ABC＝90°，
∴OB＝OP＝AB＝×4＝2，则OC＝＝＝，
∴CP＝OC﹣OP＝﹣2．
故选：B．
二、填空题（本大题共6小题，每小题4分，共24分.只要求填写最后结果）
13．（4分）纳米是一种长度单位，1纳米＝10﹣9米，冠状病毒的直径为1.2×102纳米，用科学记数法表示为 　1.2×10﹣7　米．
【解答】解：∵1纳米＝10﹣9米，
∴1.2×102纳米＝1.2×102×10﹣9米＝1.2×10﹣7米．
故答案为：1.2×10﹣7．
14．（4分）在《九章算术》中，二元一次方程组是通过“算筹”摆放的．若图中各行从左到右列出的三组算筹分别表示未知数x，y的系数与相应的常数项，如图1表示方程组是，则如图2表示的方程组是　　．

【解答】解：依题意得：．
故答案为：．
15．（4分）已知抛物线y＝ax2+bx+c如图所示，它与x轴的两交点的横坐标分别是﹣1，5．
对于下列结论：
①abc＞0；
②方程ax2+bx+c＝0的根是x1＝﹣1，x2＝5；
③9a﹣3b+c＜0；
④当x＜2时，y随着x的增大而增大．
其中正确的结论是 　②③④　（填写结论的序号）．

【解答】解：∵抛物线开口向下、顶点在y轴右侧、抛物线与y轴交于正半轴，
∴a＜0，b＞0，c＞0，
∴abc＜0，故①错误；
∵抛物线y＝ax2+bx+c与x轴的两交点的横坐标分别是﹣1，5．
∴方程ax2+bx+c＝0的根是x1＝﹣1，x2＝5，故②正确；
∵当x＝﹣3时，y＜0，
∴9a﹣3b+c＜0，故③正确；
∵抛物线y＝ax2+bx+c与x轴的两交点的横坐标分别是﹣1，5，
∴抛物线的对称轴为直线x＝＝2，
∵抛物线开口向下，
∴当x＜2时，y随着x的增大而增大，故④正确；
故答案为：②③④．
16．（4分）如图，在Rt△ABC中，∠C＝90°，分别以AB、BC、AC边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”．当AB＝8，BC＝4时，则阴影部分的面积为 　8　．

【解答】解：由勾股定理得，AB2＝AC2+BC2，
∴AC＝＝4，
则阴影部分的面积＝×AC×BC+×π×（）2+×π×（）2﹣×π×（）2
＝×4×4+×π××（AC2+BC2﹣AB2）
＝8，
故答案为：8．
17．（4分）如图，在平面直角坐标系中，点A，B，C的坐标分别为（8，0），（8，6），（0，6），点D为线段BC上一动点，将△OCD沿OD翻折，使点C落到点E处．当B，E两点之间距离最短时，点D的坐标为 　（3，6）　．

【解答】解：如图1，连接OB，
∵点A，B，C的坐标分别为（8，0），（8，6），（0，6），
∴OC＝6，OA＝BC＝8，
∴BO＝＝10，
∵BE≥OB﹣OE，
∴当O，E，B三点共线时，BE的值最小，
即当点E在对角线OB上时，BE的值最小，
如图2，∵将△OCD沿OD翻折，使点C落到点E处，
∴OE＝OC＝6，DE＝CD，∠DEO＝∠DCO＝90°，
∴∠BED＝90°，BD＝8﹣CD＝8﹣DE，
∵BD2＝DE2+BE2，
∴（8﹣DE）2＝DE2+（10﹣6）2，
解得：DE＝3，
∴CD＝DE＝3，
∴点D的坐标为（3，6），
故答案为：（3，6）．


18．（4分）如图，已知等边△ABC，D是边BC的中点，过D作DE∥AB于E，连接BE交AD于D1；过D1作D1E1∥AB于E1，连接BE1交AD于D2；过D2作D2E2∥AB于E2，…，如此继续，若记S△BDE为S1，记为S2，记为S3…，若S△ABC面积为Scm2，则Sn＝　　cm2（用含n与S的代数式表示）

【解答】解：∵D是边BC的中点，过D作DE∥AB，
∴E为AC的中点，BE⊥AC，
设△ABC的高是h，

过E作EM⊥BC于M，
∵BD＝DC，DE∥AB，
∴AE＝EC，
∵AD⊥BC，EM⊥BC，
∴AD∥EM，
∴DM＝MC，
∴EM＝AD＝h，
∴s1＝•BC•AD＝s＝，
∵DE∥AB，D1E1∥AB，
∴＝＝2＝，
∴s2＝•AE•h﹣•AE•h＝s＝，
同理s3＝s＝，
…
sn＝，
故答案为：．
三、解答题（本大题共7小题，共78分写出必要的文字说明、证明过程或推演步骤）
19．（10分）（1）先化简，再求值：（x﹣1﹣）÷，其中x＝﹣2．
（2）解不等式：﹣≤1．
【解答】解：（1）（x﹣1﹣）÷
＝•
＝
＝
＝，
当x＝﹣2时，原式＝＝1﹣2；
（2）﹣≤1，
去分母，得：2（2x﹣1）﹣3（5x+1）≤6，
去括号，得：4x﹣2﹣15x﹣3≤6，
移项及合并同类项，得：﹣11x≤11，
系数化为1，得：x≥﹣1．
20．（10分）“青年大学习”是由共青团中央发起，广大青年参与，通过学习来提升自身理论水平、思维层次的行动．梦想从学习开始，事业从实践起步．某校为了解九年级学生学习“青年大学习”的情况，随机抽取部分九年级学生进行了问卷调查，按照调查结果，将学习情况分为优秀、良好、合格、较差四个等级．学校绘制了如下不完整的统计图，根据图中信息解答下列问题：

（1）本次参与问卷调查的初中生共有　80　人，将条形统计图补充完整；
（2）扇形统计图中“合格”所对应的百分比为　30　%，“较差”所对应的圆心角度数为　36　度；
（3）该校某班有4名同学（2名男同学、2名女同学）在调查中获得“优秀”等级，班主任将从这4名同学中随机选取2名同学，代表班级参加学校组织的“青年大学习”演讲大赛，请用列表或画树状图的方法，求所选两位同学恰好是1名男同学和1名女同学的概率．
【解答】解：（1）抽取的学生人数为：16÷20%＝80（人），
抽取的学生中良好的人数为：80﹣16﹣24﹣8＝32（人），
将条形统计图补充完整如下：

故答案为：80；

（2）扇形统计图中“合格”所对应的百分比为：×100%＝30%；
“较差”所对应的圆心角度数为360°×＝36°．
故答案为：30，36；

（3）画树状图如图：

共有12个等可能的结果，所选两位同学恰好是1名男同学和1名女同学的结果有8个，
则所选两位同学恰好是1名男同学和1名女同学的概率为＝．
21．（11分）如图，一次函数y＝x+1的图象与x轴交于点A，与y轴交于点C，与反比例函数y＝（k≠0）的图象交于B，D两点，且AC＝BC．
（1）求反比例函数的解析式；
（2）已知P是x轴正半轴上一点，作PM⊥x轴交直线AB于点M，交双曲线于点N，当O，C，M，N为顶点的四边形为平行四边形时，请写出点P的坐标．

【解答】解：（1）如图1，过点B作BE⊥x轴于点E，
∵一次函数y＝x+1的图象与x轴交于点A，与y轴交于点C，
∴当x＝0时，y＝1；当y＝0时，x＝﹣2，
故A（﹣2，0），C（0，1），
∵CO⊥x轴于点O，BE⊥x轴于点E，
∴CO∥BE，
∴△AOC∽△AEB，
∵AC＝BC，
∴AO＝OE＝2，
即B点横坐标为：2，
则y＝×2+1＝2，
∴B（2，2），
∴把B点代入y＝（k≠0），
解得：xy＝4，
即y＝；
（2）如图2，由题意可得：CO∥MN，只有CO＝MN时，O，C，M，N为顶点的四边形为平行四边形，
当P点在B点右侧或D点右侧时，设P（a，0）（a＞0），则N（a，），M（a，a+1），
故MN＝a+1﹣＝CO＝1，
解得：a＝2（负值舍去）；
当P点在B点左侧或D点左侧时，设P（a，0），则N（a，），M（a，a+1），
故MN＝﹣（a+1）＝CO＝1，
解得：a＝﹣2+2（负值舍去）；
综上所述，P点坐标为（2，0）或（﹣2+2，0）．


22．（11分）我校在开学初购买了A、B两种品牌的排球，购买A品牌排球花费了2500元，购买B品牌排球花费了2000元，且购买A品牌的排球数量是购买B品牌排球数量的2倍，已知购买一个B品牌排球比购买一个A品牌排球多花30元．
（1）求购买一个A品牌、一个B品牌的排球各需多少元？
（2）学校决定再次购进A、B两种品牌排球共50个，恰逢两种品牌排球的售价进行调整，A品牌排球售价比第一次购买时提高了8%，B品牌排球按第一次购买时售价的9折出售，如果学校第二次购买A、B两种品牌排球的总费用不超过3240元，那么学校第二次最多可购买多少个B品牌排球？
【解答】解：（1）设购买一个A品牌排球需要x元，则购买一个B品牌排球需要（x+30）元，
依题意得：＝2×，
解得：x＝50，
经检验，x＝50是原方程的解，且符合题意，
∴x+30＝50+30＝80．
答：购买一个A品牌排球需要50元，购买一个B品牌排球需要80元．
（2）设学校第二次最多可购买m个B品牌排球，则购买（50﹣m）个A品牌排球，
依题意得：50×（1+8%）（50﹣m）+80×0.9m≤3240，
解得：m≤30．
又∵m为正整数，
∴m可以取的最大值为30．
答：学校第二次最多可购买30个B品牌排球．
23．（12分）在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．
（1）如图1所示，点M，N分别在线段AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝时，求线段AM的长；
（2）如图2所示，点E，F分别在AB，AC上，且BE＝AF，求证：△DEF是等腰直角三角形；
（3）如图3所示，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+AN＝AM．
【解答】（1）解：∵∠BAC＝90°，AB＝AC，AD⊥BC，
∴AD＝BD＝DC，∠ABC＝∠ACB＝45°，∠BAD＝∠CAD＝45°，
∵AB＝，
∴AD＝BD＝DC＝AB＝×＝，
∵∠AMN＝30°，
∴∠BMD＝180°﹣90°﹣30°＝60°，
∴∠MBD＝90°﹣60°＝30°，
∴BM＝2DM，
由勾股定理得，BM2﹣DM2＝BD2，
即（2DM）2﹣DM2＝（）2，
解得：DM＝1，
∴AM＝AD﹣DM＝﹣1；
（2）证明：如图2，由（1）得：∠DAF＝∠DBE＝45°，AD＝BD，
又∵BE＝AF，
∴△DAF≌△DBE（SAS），
∴DF＝DE，∠ADF＝∠BDE，
∵AD⊥BC，
∴∠ADB＝90°，
即∠BDE+∠ADE＝90°，
∴∠ADF+∠ADE＝90°，
即∠EDF＝90°，
又∵DF＝DE，
∴△DEF是等腰直角三角形；
（3）证明：过点M作MP⊥AM，交AB的延长线于点P，如图3所示：
∴∠AMP＝90°，
∵∠PAM＝45°，
∴∠P＝∠PAM＝45°，
∴AM＝PM，
∵∠BMN＝∠AMP＝90°，
∴∠BMP＝∠AMN，
又∵∠DAC＝∠P＝45°，AM＝PM，
∴△AMN≌△PMB（ASA），
∴AN＝PB，
∴AP＝AB+BP＝AB+AN，
在Rt△AMP中，∠AMP＝90°，AM＝MP，
∴AP＝AM，
∴AB+AN＝AM．


24．（12分）已知抛物线y＝ax2+bx+c（a≠0）经过A（4，0）、B（﹣1，0）、C（0，4）三点．

（1）求抛物线的函数解析式；
（2）如图1，点D是在直线AC上方的抛物线的一点，DN⊥AC于点N，DM∥y轴交AC于点M，求△DMN周长的最大值及此时点D的坐标；
（3）如图2，点P为第一象限内的抛物线上的一个动点，连接OP，OP与AC相交于点Q，求的最大值．
【解答】解：（1）法一：依题意，得，
解之，得，
∴抛物线解析式为y＝﹣x2+3x+4．
法二：依题意，得y＝a（x﹣4）（x+1）（a≠0），
将C（0，4）坐标代入得，
﹣3a＝3，
解得a＝﹣1，
∴抛物线解析式为y＝﹣x2+3x+4．
法三：依题意，得，
解之，得，
∴抛物线解析式为y＝﹣x2+3x+4．
（2）如图1，延长DM交x轴于点H，

∵OA＝OC＝4，OA⊥OC，DM∥y轴交AC于点M，
∴∠OAC＝45°，∠AHM＝90°，
∵DN⊥AC于点N，
∴∠AMH＝∠DMN＝45°，
∴△DMN是等腰直角三角形，
∴．
设直线AC的解析式为y＝kx+b'（k≠0），
将A（4，0）、C（0，4）两点坐标代入得，
解得，
所以直线AC的解析式为y＝﹣x+4，
设D（m，﹣m2+3m+4），
∴M（m，﹣m+4），
∴DM＝﹣m2+3m+4﹣（﹣m+4）＝﹣m2+4m＝﹣（m﹣2）2+4，
∴当m＝2时，DM最大值为4，
此时D（2，6），
∵△DMN是等腰直角三角形，
∴△DMN周长＝，
∴△DMN周长的最大值为，
此时D（2，6）．
（3）法一：如图2，过PM∥y轴交AC于点M，

设P（m，﹣m2+3m+4），
∴M（m，﹣m+4），
∴PM＝﹣m2+3m+4﹣（﹣m+4）＝﹣m2+4m＝﹣（m﹣2）2+4，
∵PM∥OC，
∴，
∴，
∵，
∴当m＝2时，的最大值为1．
法二：如图2，设Q（m，﹣m+4），P（n，﹣n2+3n+4），

∴．
设直线OP的解析式为y＝kx（k≠0），
将Q（m，﹣m+4）点代入得，
∴直线OP的解析式，
将P（n，﹣n2+3n+4）坐标代入得，，
所以，
化简得，
∴，
∵
∴当n＝2时，的最大值为1．
25．（12分）如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且CF是⊙O的切线．
（1）求证：∠DCF＝∠CAD．
（2）探究线段CF，FD，FA的数量关系并说明理由；
（3）若cosB＝，AD＝2，求FD的长．

【解答】（1）证明：如图，连接OC，
∵AD是⊙O的直径，
∴∠ACD＝90°，
∴∠OCD+∠OCA＝90°，
∵FC是⊙O的切线，
∴∠DCF+∠OCD＝90°，
∴∠OCA+∠DCF，
∵OC＝OA，
∴∠CAD＝∠OCA，
∴∠DCF＝∠CAD；
（2）解：FC2＝FD•FA，理由如下：
∵∠FCD＝∠FAC，∠F＝∠F，
∴△FCD∽△FAC，
∴＝，
∴FC2＝FD•FA；
（3）解：∵∠B＝∠ADC，cosB＝，
∴cos∠ADC＝，
在Rt△ACD中，
∵cos∠ADC＝＝，
∴＝，
由（2）知△FCD∽△FAC，
∴＝＝＝，
∴FC2＝FD•FA，
设FD＝3x，则FC＝4x，AF＝3x+2，
又∵FC2＝FD•FA，
即（4x）2＝3x（3x+2），
解得x＝（取正值），
∴FD＝3x＝．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/6/4 11:28:18；用户：朱文磊；邮箱：fywgy23@xyh.com；学号：21522783