人教A版 (2019)必修 第二册7.1 复数的概念多媒体教学ppt课件

这是一份人教A版 (2019)必修 第二册7.1 复数的概念多媒体教学ppt课件，共34页。PPT课件主要包含了必备知识生成，虚数单位，复数集，ac且bd，关键能力探究，课堂素养达标等内容，欢迎下载使用。

【情境探究】1.回顾一元二次方程的解,明确实数的概念与分类:(1)方程x2-2x-3=0的正整数解是__,有理数解是_____,实数解是_____.(2)方程x2-2x-1=0的无理数解是 ,实数解是 .
2.(1)方程x2=-1在实数集中是否有解?提示:因为实数的平方都是非负数,所以方程x2=-1在实数集中无解.(2)为了解决此类方程无实数解的问题,我们引入新数i,定义i·i=i2=-1,将实数集加以扩充,得到一个新的数集,那么此方程在这个数集中就有一个解为__.
3.(1)复数a+bi(a,b∈R)何时表示零?提示:当且仅当a=b=0时表示零.(2)实数集R与复数集C有什么关系?提示:用文字语言描述:实数集R是复数集C的真子集,即R C.用图形语言描述:
【知识生成】1.数系的扩充与复数的概念:(1)复数的定义形如_____________的数叫做复数,其中i叫做_________,满足i2=___,全体复数所构成的集合C={a+bi|a,b∈R}叫做_______.(2)复数的表示复数通常用字母z表示,即z=_____________,a与b分别叫做复数z的_____与_____.(3)复数相等设a,b,c,d都是实数,那么a+bi=c+di⇔_________.
a+bi(a,b∈R)
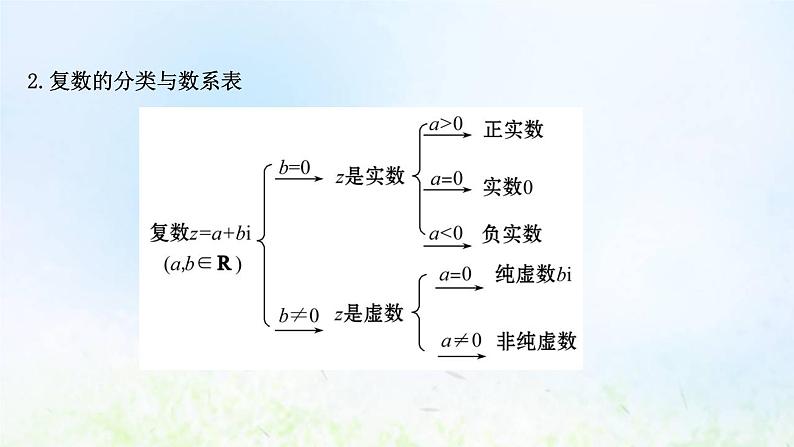
2.复数的分类与数系表
探究点一　复数的有关概念与表示【典例1】1.给出下列三个命题:①若z∈C,则z2≥0;②2i-1虚部是2i;③2i的实部是0.其中真命题的个数为(　　)A.0　　　　B.1　　　　C.2　　　　D.32.已知复数z=a2-(2-b)i的实部和虚部分别是2和3,则实数a,b的值分别是________、________. 3.判断下列命题的真假.①若实数a与ai对应,则实数集与纯虚数集一一对应;②实数集的补集是虚数集.
【思维导引】利用复数的概念判断.【解析】1.选B.对于①,当z∈R时,z2≥0成立,否则不成立,如z=i,z2=-1<0,所以①为假命题;对于②,2i-1=-1+2i,其虚部为2,不是2i,所以②为假命题;对于③,2i=0+2i,其实部是0,所以③为真命题.
2.由题意得:a2=2,-(2-b)=3,所以a=± ,b=5.答案:± 　53.①当a=0时,ai=0为实数,故①为假命题.②由复数集的分类知,②正确,是真命题.
【类题通法】判断与复数有关的命题是否正确的策略(1)复数的代数形式:若z=a+bi,只有当a,b∈R时,a才是z的实部,b才是z的虚部,且注意虚部不是bi,而是b.(2)不要将复数与虚数的概念混淆,实数也是复数,实数和虚数是复数的两大构成部分.(3)举反例:判断一个命题为假命题,只要举一个反例即可,所以解答这类题时,可按照“先特殊,后一般,先否定,后肯定”的方法进行解答.
【定向训练】1.已知纯虚数z=(a-1)+(a-b)i,则实数a,b满足的条件是(　　)A.a=1,b=1B.a≠1,b=1C.a≠1,b≠1D.a=1,b≠1【解析】选D.因为纯虚数z=(a-1)+(a-b)i,则a-1=0,且a-b≠0,所以a=1,b≠1.
2.已知复数z=(a-1)-(2-b)i的实部和虚部分别是2和1,则实数a,b的值分别是________. 【解析】由题意得:a-1=2,-(2-b)=1,所以a=3,b=3.答案:3,3
探究点二　复数的分类【典例2】1.已知x∈R,复数z=(x2-1)+(x+1)i为纯虚数,则z=________. 2.已知m∈R,复数z= +(m2+2m-3)i,当m为何值时,z分别满足下列条件?(1)z∈R;(2)z是虚数;(3)z是纯虚数.
【思维导引】 z=a+bi⇒
【解析】1.由于复数z=(x2-1)+(x+1)i为纯虚数,则实数x满足 解得x=1,所以z=2i.答案:2i 2.复数z= +(m2+2m-3)i,m∈R.(1)由z∈R,得 解得m=-3. (2)由z是虚数,得m2+2m-3≠0且m-1≠0,解得m≠1且m≠-3.
(3)由z是纯虚数,得解得m=0或m=-2.
【类题通法】1.解决复数分类问题的方法与步骤(1)化标准式:解题时一定要先看复数是否为a+bi(a,b∈R)的形式,以确定实部和虚部.(2)定条件:复数的分类问题可以转化为复数的实部与虚部应该满足的条件问题,列出实部和虚部满足的方程(不等式)组即可.(3)下结论:设所给复数为z=a+bi(a,b∈R),①z为实数⇔b=0;②z为虚数⇔b≠0;③z为纯虚数⇔a=0且b≠0.
2.复数分类的应用(1)参数自身:判断一个含有参数的复数在什么情况下是实数、虚数、纯虚数,首先要保证参数值使表达式有意义,其次对参数值的取舍,是取“并”还是“交”,非常关键,解答后进行验证是很必要的.(2)整体与局部:对于复数z=a+bi(a,b∈R),既要从整体的角度去认识它,把复数z看成一个整体,又要从实部与虚部的角度分解成两部分去认识它.这是解复数问题的重要思路之一.
【定向训练】1.若复数z=(m+1)+(m2-9)i<0,则实数m的值等于________. 【解析】因为z<0,所以 所以m=-3.答案:-3
2.已知复数z=m(m-1)+(m2+2m-3)i,当实数m取什么值时,复数z是(1)零;(2)纯虚数.【解析】(1)因为z是零,所以 解得m=1.(2)因为z是纯虚数,所以 解得m=0.综上,当m=1时,z是零;当m=0时,z是纯虚数.
【补偿训练】下列复数中,实数为________,虚数为________,纯虚数为________. (将序号填在相应的横线上)①1+2i;②1-2i2;③-3i;④2i-3;⑤1+0i;⑥cs π+isin π.【解析】1+2i,-3i,2i-3是虚数;-3i是纯虚数;1-2i2=3,1+0i=1,cs π+isin π=-1,都是实数.答案:②⑤⑥　①③④　③
探究点三　复数相等及其应用【典例3】1.已知复数z1=a+2i,z2=2(1+bi),若z1=z2,则实数a,b的值分别为 (　　)　　　　　　 　　　　　　 　　　　　　 A.a=1,b=1B.a=1,b=2C.a=2,b=1D.a=2,b=22.已知关于x的方程x2+(1-2i)x+(3m-i)=0有实数根,求实数m的值及方程的实数根.
【思维导引】1.根据复数相等的充要条件:实部与虚部分别相等求a,b的值.2.设出方程的实数解,代入原式整理为a+bi=0(a,b∈R)的形式解决.
【解析】1.选C.因为复数z1=a+2i,z2=2+2bi,且z1=z2,则实数a=2,2b=2,即a=2,b=1.2.设a是原方程的实数根,则a2+(1-2i)a+(3m-i)=0,即(a2+a+3m)-(2a+1)i=0+0i,所以a2+a+3m=0且2a+1=0,所以 且所以所以 ,方程的实数根为
【类题通法】 复数相等问题的解题技巧(1)必须是复数的代数形式才可以根据实部与实部相等,虚部与虚部相等列方程组求参数的解.(2)根据复数相等的条件,将复数问题转化为实数问题,为应用方程思想提供了条件,同时这也是复数问题实数化思想的体现.(3)如果两个复数都是实数,可以比较大小,否则两个虚数不能比较大小.
【定向训练】已知M={1,(m2-2m)+(m2+m-2)i},P={-1,1,4i},若M∪P=P,则实数m的值为_____. 【解析】因为M∪P=P,所以M⊆P.由(m2-2m)+(m2+m-2)i=-1,得 解之得m=1.或由(m2-2m)+(m2+m-2)i=4i,得 解之得m=2.综上可知m=1或m=2.答案:1或2
【补偿训练】求适合等式(2x-1)+i=y+(y-3)i的x,y的值.其中x∈R,y∈R.【解析】由复数相等的充要条件可知 解得
数系的扩充和复数的概念
1.数系的扩充.2. 复数有关的概念
(1)判断复数是实数、虚数或者纯虚数：①保证复数的实部、虚部均有意义．②根据分类的标准，列出实部、虚部应满足的关系式再求解．(2)复数相等求参数的步骤：分别确定两个复数的实部与虚部， 利用实部与实部、虚部与虚部分别相等，列方程组求解．
(1)两个复数不全是实数，就不能比较大小．(2)一个数的平方非负在实数范围内是真命题，在复数范围内是假命题.(3)对于复数实部、虚部的确定不但要把复数化为a＋bi的形式，更要 注意这里a，b均为实数时，才能确定复数的实、虚部．
1.数学抽象：复数及相关概念.2.逻辑推理：复数的分类.3.数学运算：复数相等求参数.
1、复数的代数形式.2、复数的实部、虚部.3、虚数、纯虚数.4、复数相等.
1.复数z=(m2+m)+mi(m∈R,i为虚数单位)是纯虚数,则实数m的值为(　　)A.0或-1　　B.0　　　　C.1　　　　D.-1【解析】选D.因为z为纯虚数,所以 所以m=-1.
2.下列命题中,正确命题的个数是(　　)①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;②若a,b∈R且a>b,则a+i>b+i;③若x2+y2=0,则x=y=0.A.0　　　　　B.1　　　　　C.2　　　　　D.3
【解析】选A.①由于x,y∈C,所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,①是假命题.②由于两个虚数不能比较大小,所以②是假命题.③当x=1,y=i时,x2+y2=0成立,所以③是假命题.
3.已知x是方程x2=-1的解,则1+x=(　　)A.1+iB.1-iC.1±iD.0【解析】选C.由x2=-1,可知x=±i,所以1+x=1±i.