2021学年4.4 平行线的判定测试题
展开
4.4平行线的判定
(限时70分钟 满分120分)
一、单选(共计6小题,每小题5分,共30分)
1.下面3个命题:①同旁内角互补;②两直线平行,内错角相等;③在同一平面内,垂直于同一直线的两直线互相平行,其中真命题为( )
A.① B.③ C.②③ D.②
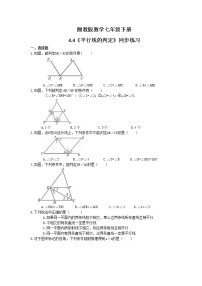
2.如图,直线a,b都与直线c相交,给出的下列条件:①∠1=∠7;②∠3=∠5;③∠1+∠8=180°;④∠3=∠6.其中能判断a∥b的是( )
A.①③ B.②③ C.③④ D.①②③
3.如图,下列说法中,正确的是( )
A.因为∠A+∠D=180°,所以AD∥BC
B.因为∠C+∠D=180°,所以AB∥CD
C.因为∠A+∠D=180°,所以AB∥CD
D.因为∠A+∠C=180°,所以AB∥CD
4.如图,能判定EC∥AB的条件是( )
A.∠B=∠ACB B.∠A=∠ACE C.∠B=∠ACE D.∠A=∠ECD
5.如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
A.∠1=∠4 B.∠3=∠2
C.∠1=∠2 D.∠1与∠2互补
6.如图,下列条件中,不能判断直线a∥b的是( )
A.∠1+∠3=180° B.∠2=∠3
C.∠4=∠5 D.∠4=∠6
二、填空(共计6小题,每空5分,共30分)
7.没有公共顶点的两个直角,如果它们有一边在同一直线上,那么它们的另一边相互 .
8.如图,四边形 中, ,连接 , 平分 ,E是直线 上一点, , ,则 的长为 .
9.如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
10.如图,已知直线c与a,b均相交,若直线a∥b需要添加条件
11.在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,则下面三个结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是 .
12.如图,BC=EF,AC∥DF。请你添加一个适当的条件,使得△ABC≌△DEF。 (只需填一个答案即可)
三、解答(共计5小题,共60分)
13.(10分)请把下列证明过程补充完整.
已知:如图,BCE,AFE是直线, , , ,
求证:
证明: 已知
▲ ▲
已知
▲ 等量代换
已知
▲
即 ▲
▲ 等量代换
▲
14.(10分)已知:如图,CD⊥AB于D,DE∥BC,EF⊥AB于F,求证:∠FED=∠BCD.
15.(10分)如图, , 于G,证明 .
16.(15分)小明在学习三角形内角和定理时,由于病假缺课,只知道三角形内角和为180度,却不知道原理。请同学们帮他补习一下,完成定理证明。已知:如图,△ABC中,∠A、∠B、∠C是它的三个内角,请证明∠A+∠B+∠C=180°.
17.(15分)如图,若 , ,试说明 的理由.
答案
1.C
2.D
3.C
4.B
5.C
6.C
7.平行.
8.6或10
9.55°
10.∠1=∠4(答案不唯一)
11.①②
12.AC=DF(或AB∥DE,或∠A=∠D,或∠B=∠DEC)
13.证明: 已知
两直线平行,内错角相等
已知
等量代换
已知
等式性质
即
等量代换
同位角相等,两直线平行 .
14.证明:∵CD⊥AB,EF⊥AB,∴CD∥EF,∴∠FED=∠EDC,∵DE∥BC,∴∠EDC=∠BCD,∴∠FED=∠BCD
15.解:∵
∴
∵
∴
16.证明:如图,
作∠ACD=∠A,并延长BC到E,
∵∠1=∠A
∴AB∥CD
∴∠B=∠2,
∵∠ACB+∠1+∠2=180°
∴∠ACB+∠A+∠B=180°.
17.证明:∵ ,
∴∠DCA=∠BAC,
∵ ,
∴∠3=∠4,
∴CE∥AF,
∴ .
湘教版七年级下册第4章 相交线与平行线4.4 平行线的判定优秀同步练习题: 这是一份湘教版七年级下册第4章 相交线与平行线4.4 平行线的判定优秀同步练习题,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学湘教版七年级下册4.4 平行线的判定精品课堂检测: 这是一份初中数学湘教版七年级下册4.4 平行线的判定精品课堂检测
初中数学湘教版七年级下册4.4 平行线的判定同步达标检测题: 这是一份初中数学湘教版七年级下册4.4 平行线的判定同步达标检测题,共8页。试卷主要包含了4平行线的判定等内容,欢迎下载使用。