江苏省连云港市宁海中学2021-2022学年八年级下学期期中质量调研数学试卷(word版含答案)

2021—2022学年度第二学期期中学业质量调研

八年级数学

注意事项：

1．本试卷共4页．全卷满分150分．考试时间为100分钟．考生答题全部答在答题纸上，答在本试卷上无效．

2．作图必须用2B铅笔作答，并请加黑加粗，描写清楚．

一、选择题（每小题3分,满分24分）

1．下列图形中，既是轴对称图形又是中心对称图形的是（▲）

A． B． C． D．

2．某学习小组为了了解本校2000名学生的视力情况，随机抽查了500名学生，其中有200名学生近视．对于这个问题上，下列说法中正确的是（▲）

A．每名学生是总体的一个个体 

B．样本容量是500 

C．样本是500名学生 

D．该校一定有1000名学生近视

3．下列调查中，比较适合使用抽样调查的是（▲）

A．检查人造卫星重要零部件的质量 

B．对某本书中的印刷错误的调查 

C．长江中现有鱼的种类 

D．在防疫新冠病毒期间，对进入学校的人员进行体温检测

4．下面条件中，能判定四边形是平行四边形的条件是（▲）

A．一组对角相等 B．对角线互相平分 

C．一组对边相等 D．对角线互相垂直

5．如果把分式中的x和y都扩大为原来的2倍，那么分式的值（▲）

A．扩大为原来的4倍 B．扩大为原来的2倍 

C．不变 D．缩小为原来的

6．菱形具有而矩形不具有的性质是（▲）

A．对角线互相平分 B．对角相等 

C．对角线互相垂直 D．对边平行且相等

7．如图，将△ABC绕点B顺时针旋转角α，得到△A1BC1，此时点A，点B，点C1在一条直线上，若∠A1BC＝22°，则旋转角α＝（▲）

A．79° B．80° C．78° D．81°

8．如图，△ABC中，AD平分∠BAC，E是BC中点，AD⊥BD，AC＝7，AB＝4，则DE的值为（▲）

A．1 B．2 C． D．

二、填空题（每小题4分，满分40分）

9．一只不透明的袋子中有1个红球、1个黑球和2个白球，这些球除颜色不同外其它都相同，搅匀后从中任意摸出1个球，摸出白球可能性   ▲   摸出红球可能性（填“等于”或“小于”或“大于”）．

10．为了直观地表示世界七大洲的面积各占全球陆地面积的百分比，最适合使用的统计图

是   ▲   统计图．

11．要使分式有意义，则x的取值范围是   ▲   ．

12．约分：＝   ▲   ．

13．某种油菜籽在相同条件下发芽试验的结果如表：

那么这种油菜籽发芽的概率是   ▲   （结果精确到0.01）．

14．我们把一个样本的40个数据分成4组，其中第1、2、3组的频数分别为6、12、14，则

    第4组的频率为   ▲   ．

15．在□ABCD中，∠B+∠D＝100°，则∠A等于   ▲   ．

16．若菱形的对角线长分别是8和10，则菱形的面积是   ▲   ．

17．如图，已知□ABCD三个顶点坐标是A（﹣1，0）、B（﹣2，﹣3）、C（2，﹣1），那么

    第四个顶点D的坐标是   ▲   ．

18．正方形ABCD的边长为12，点E在BC上，且BE＝5，点P是对角线BD上的一个动点，

   则PE+PC的最小值是   ▲   ．

三、解答题（本大题共8题，满分86分）．

19．（本题满分15分）约分：

⑴    ⑵     ⑶

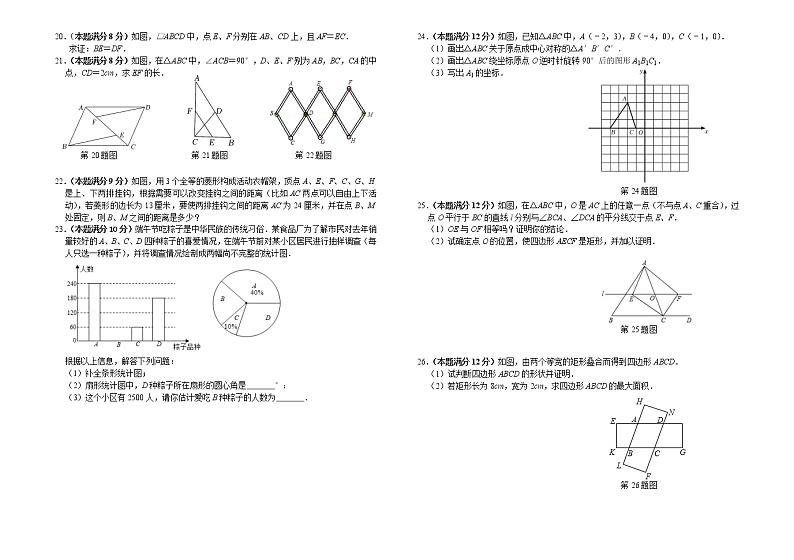
20．（本题满分8分）如图，□ABCD中，点E、F分别在AB、CD上，且AF＝EC．

求证：BE＝DF．

21．（本题满分8分）如图，在△ABC中，∠ACB＝90°，D、E、F别为AB，BC，CA的中点，CD＝2cm，求EF的长．

22．（本题满分9分）如图，用3个全等的菱形构成活动衣帽架，顶点A、E、F、C、G、H是上、下两排挂钩，根据需要可以改变挂钩之间的距离（比如AC两点可以自由上下活动），若菱形的边长为13厘米，要使两排挂钩之间的距离AC为24厘米，并在点B、M处固定，则B、M之间的距离是多少？

23．（本题满分10分）端午节吃粽子是中华民族的传统习俗．某食品厂为了解市民对去年销量较好的A、B、C、D四种粽子的喜爱情况，在端午节前对某小区居民进行抽样调查（每人只选一种粽子），并将调查情况绘制成两幅尚不完整的统计图．

根据以上信息，解答下列问题：

（1）补全条形统计图；

（2）扇形统计图中，D种粽子所在扇形的圆心角是　   　°；

（3）这个小区有2500人，请你估计爱吃B种粽子的人数为　   　．

24．（本题满分12分）如图，已知△ABC中，A（﹣2，3），B（﹣4，0），C（﹣1，0）．

（1）画出△ABC关于原点成中心对称的△A′B′C′．

（2）画出△ABC绕坐标原点O逆时针旋转90°后的图形A1B1C1．

（3）写出A1的坐标．

25．（本题满分12分）如图，在△ABC中，O是AC上的任意一点（不与点A、C重合），过点O平行于BC的直线l分别与∠BCA、∠DCA的平分线交于点E、F．

（1）OE与OF相等吗？证明你的结论．

（2）试确定点O的位置，使四边形AECF是矩形，并加以证明．

26．（本题满分12分）如图，由两个等宽的矩形叠合而得到四边形ABCD．

（1）试判断四边形ABCD的形状并证明．

（2）若矩形长为8cm，宽为2cm，求四边形ABCD的最大面积．

2021—2022学年度第二学期期中学业质量调研

八年级数学

参考答案及评分建议

一．选择题（每小题3分，共24分）

二、填空题（每小题3分，共30分）

9．大于     10．扇形    11．x≠﹣1      12．        13．0.95

14．0.2      15．130°   16．40         17．（3，2）    18．13

19．（本题满分15分）

解：（1）＝………………………………2分

=………………………………………… 5分

（2）＝…………………………………… 3分

=m；…………………………………………………5分

（3）＝ …………………………… 3分

=．………………………………………… 5分

20．（本题满分8分）

证明：∵四边形ABCD是平行四边形，

∴AD＝CB，AD∥CB，…………………………………2分

∴∠DAF＝∠BCE，……………………………………4分

在△DAF和△BCE中，

，

∴△DAF≌△BCE（SAS），…………………………6分

∴BE＝DF．……………………………………………8分

21．（本题满分8分）

解：在Rt△ABC中，∠ACB＝90°，D为AB中点，CD＝2cm，

∴AB＝2CD＝4cm，………………………………… 3分

∵E，F分别为BC，CA的中点，

∴EF是△ABC的中位线，……………………………………………………5分

∴EF＝AB＝2cm．………………………………………………………… 8分

22．（本题满分9分）解：连接AC，BD交于点O，

∵四边形ABCD是菱形，

∴AO＝AC＝12厘米，AC⊥BD，…………………………………………4分

∴BO＝＝＝5厘米，……………………………6分

∴BD＝2BO＝10厘米，…………………………………………………… 8分

∴BM＝3BD＝30厘米．…………………………………………………… 9分

23．（本题满分10分）

（1）补全条形统计图；……………………………………………………3分

（2）扇形统计图中，D种粽子所在扇形的圆心角是　108　°；…… 6分

（3）这个小区有2500人，请你估计爱吃B种粽子的人数为　500　．

…………………………………………………………………………10分

24．（本题满分12分）

解：（1）如图，△A′B′C′为所作；………………………………4分

（2）如图，△A1B1C1为所作；…………………………………………8分

（3）A1的坐标为（﹣3，﹣2）．…………12分

25．（本题满分12分）

（1）解：相等；理由是：∵直线l∥BC，

∴∠OEC＝∠ECB，………………………1分

∵CE平分∠ACB，

∴∠OCE＝∠BCE，…………………… 2分

∴∠OEC＝∠OCE，…………………… 3分

∴OE＝OC，…………………………… 4分

同理OF＝OC，…………………………5分

∴OE＝OF．…………………………… 6分

（2）解：O在AC的中点上时，四边形AECF是矩形，

  ………………………………………  8分

理由是：∵OA＝OC，OE＝OF，

∴四边形AECF是平行四边形，………10分

∵OE＝OF＝OC＝OA，

∴AC＝EF，

∴平行四边形AECF是矩形．……… 12分

26．（本题满分12分）

解：（1）四边形ABCD是菱形．……2分

理由：作AR⊥BC于R，AS⊥CD于S，

由题意知：AD∥BC，AB∥CD，

∴四边形ABCD是平行四边形，……3分

∵两个矩形的宽度相等，

∴AR＝AS，……………………………………………………………4分

∵AR•BC＝AS•CD，

∴BC＝CD，………………………………………………………… 5分

∴平行四边形ABCD是菱形；………………………………………6分

（2）当这两张纸片叠合成如图2时，菱形的面积最大，

设BC＝x，则CG＝8﹣x，CD＝BC＝x，

在Rt△CBG中，CG2+BG2＝BC2，

∴（8﹣x）2+22＝x2，………………………………………………9分

解得x＝，………………………………………………………11分

∴S＝BG•DG＝．………………………………………………12分