初中数学苏科版七年级下册10.4 三元一次方程组教学设计

这是一份初中数学苏科版七年级下册10.4 三元一次方程组教学设计，共4页。教案主要包含了 情景引入等内容，欢迎下载使用。
1.理解三元一次方程组的概念．
能解简单的三元一次方程组，在解的过程中进一步体会“消元”的基本思想.
教学重点
1．使学生会解简单的三元一次方程组．
2．通过本节学习，进一步体会“消元”的基本思想．
教学难点
针对方程组的特点，灵活使用代入法、加减法等重要方法．
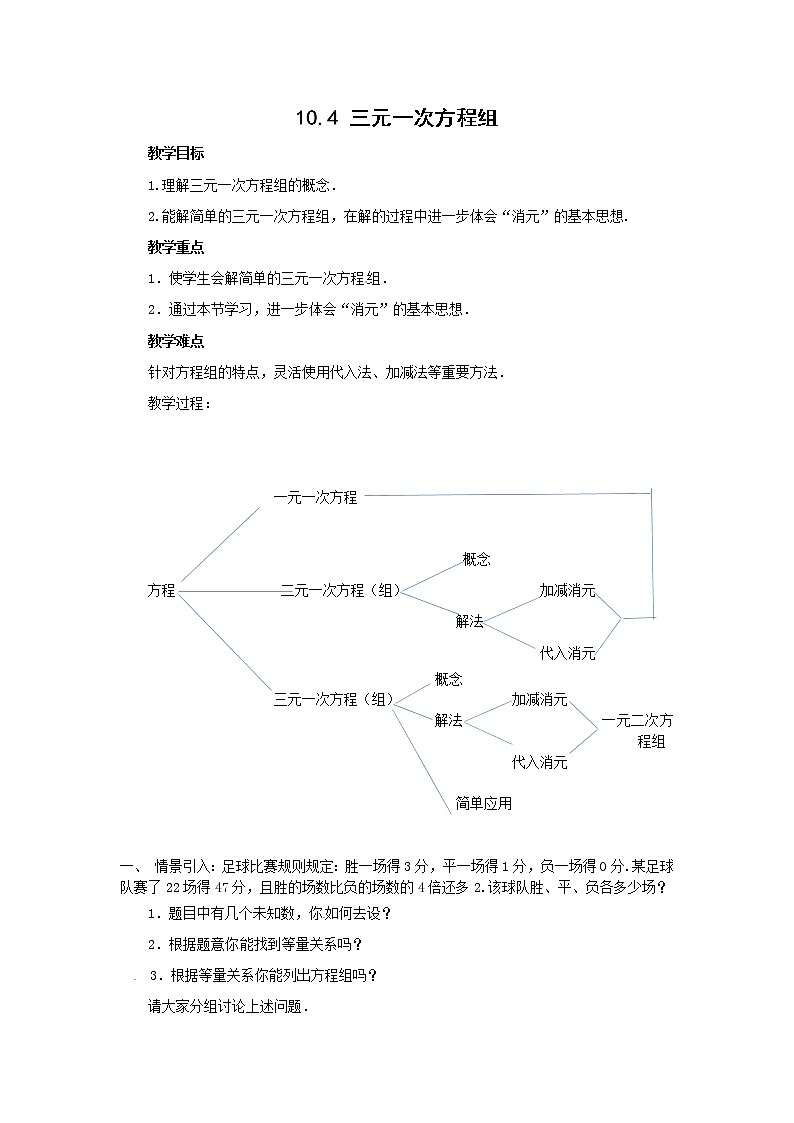
教学过程：
一元一次方程
概念
方程 二元一次方程（组） 加减消元
解法
代入消元
概念
三元一次方程（组） 加减消元
解法 一元二次方程组
代入消元
简单应用
一、 情景引入：足球比赛规则规定：胜一场得3分，平一场得1分，负一场得0分.某足球队赛了22场得47分，且胜的场数比负的场数的4倍还多2.该球队胜、平、负各多少场？
1．题目中有几个未知数，你如何去设？
2．根据题意你能找到等量关系吗？
3．根据等量关系你能列出方程组吗？
请大家分组讨论上述问题．
（教师对学生进行巡回指导）
学生成果展示：
{
解：设该球队胜x场，平y场，负z场
师：这个方程组和前面学过的二元一次方程组有什么区别和联系？
生：这个方程组有三个相同的未知数，每个方程中含未知数的项的次数都是1，并且一共有三个方程，像这样的方程组叫做三元一次方程组．
师： 怎样解这个方程组呢？能不能类比二元一次方程组的解法，设法消去一个或两个未知数，把它化成二元一次方程组或一元一次方程呢？
（学生小组交流，探索如何消元．）
可以把③分别代入①②，便消去了x，只包含y和z二元了，
解此二元一次方程组得出y、z，进而代回原方程组可求x．
教师对学生的想法给予肯定并总结解三元一次方程组的基本思路：通过“代入”或“加减”进行消元，把“三元”化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而转化为解一元一次方程．
即三元一次方程组 二元一次方程组 一元一次方程
例题讲解
{
解方程组
请同学们分别用加减消元和代入消元法解方程组.
归纳：此方程组的特点是③不含y，而①②中y的系数为整数倍关系，因此用加减法从①②中消去y后，再与③组成关于x和z的二元一次方程组的解法最合理．
例2：在等式y=ax2+bx+c中，当x=-1时，y=0；当x=2时，y=3；当x=5时，y=60，求a，b，c的值．
（师生一起分析，列出方程组后交由学生求解．）
解：由题意，得三元一次方程组
②-①，得a+b=1， ④
③-①，得4a+b=10． ⑤
④与⑤组成二元一次方程组．
解得
把a=3，b=-2代入①，得c=-5．
因此，
答：a=3，b=-2，c=-5．
x＋y－z＝11，
y＋z－x＝5，
z＋x－y＝1.
①
②
③
当堂练习
解方程组

则x＝_____，y＝______，z＝_______.
2.若x＋2y＋3z＝10，4x＋3y＋2z＝15，则x＋y＋z的值为（ ）
A.2 B.3 C.4 D.5
总结提炼
解三元一次方程组的基本思路是：通过“代入”或“加减”进行消元，把“三元”转化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而再转化为解一元一次方程．
三元一次方程组
二元一次方程组
一元一次方程
消元
消元