专题02 垂径定理在圆中的应用-2021-2022学年九年级数学上册难点突破（人教版）

专题02 垂径定理在圆中的应用

圆的定义：

1．在同一平面内，线段OP绕着它固定的一个端点O旋转一周，另一端点P所经过的封闭曲线叫做圆．

2．圆是到定点距离等于定长的点的集合．

圆的基本性质：

1．圆是轴对称图形：任何一条直径所在的直线都是它的对称轴．

2．垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧．

推论：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧．

3．同圆或等圆中，两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等，它们所对应的其余各组量也分别相等．

确定圆的条件：

确定一个圆必须明确两个要素：①圆心(决定圆的位置)；②半径(决定圆的大小)．

点和圆的位置关系：

点P在圆内⇔d＜r；

点P在圆上⇔d＝r；

点P在圆外⇔d＞r.

垂径定理

1．与弦有关的题目，要求解边与角时，连结半径构造等腰三角形是常用的辅助线．

2．求圆中的弦长时，通常作辅助线，由半径、弦的一半以及弦心距构成直角三角形运用勾股定理进行求解．

圆的基本性质中常见的

基本图形

圆心角定理

在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．

1°弧的概念

1°圆心角所对的弧叫做1°弧．

一、圆的概念

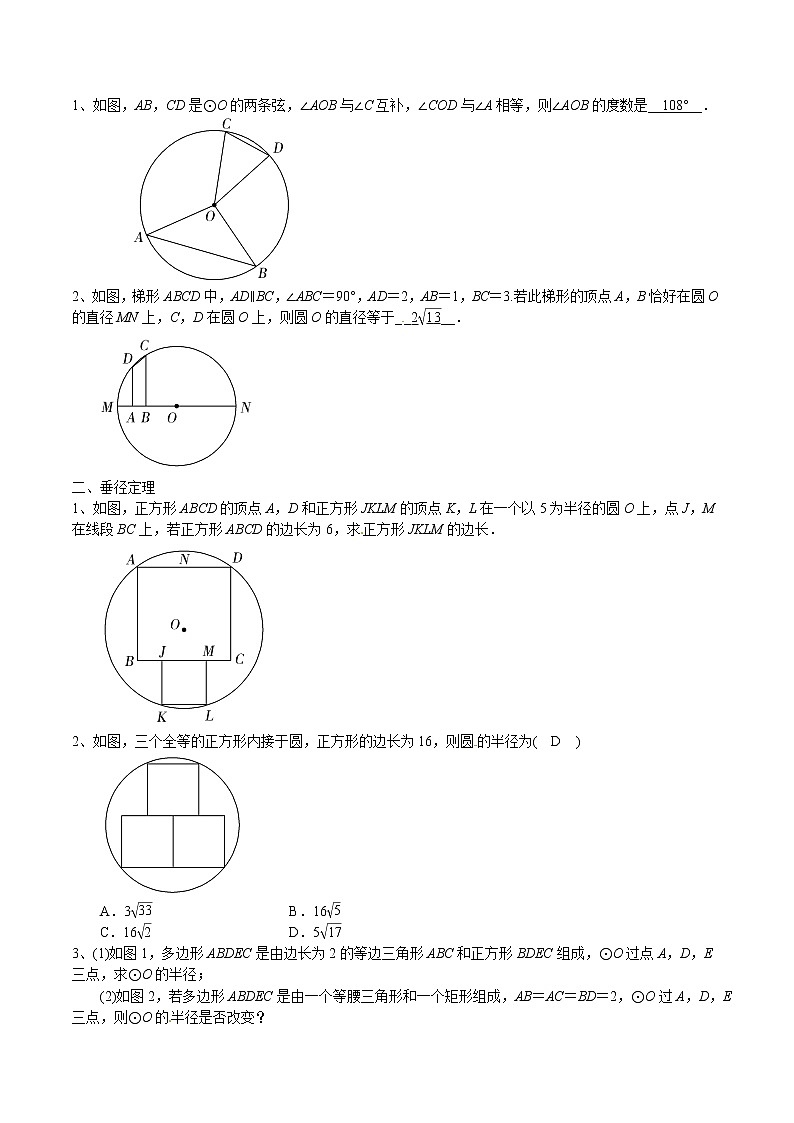
1、如图，AB，CD是⊙O的两条弦，∠AOB与∠C互补，∠COD与∠A相等，则∠AOB的度数是__108°__．

【解析】 ∵∠AOB与∠C互补，

∴∠C＝∠D＝180°－∠AOB，

∴∠COD＝180°－2∠C＝2∠AOB－180°，

∵∠A＝∠B＝(180°－∠AOB)，∠COD＝∠A，

∴2∠AOB－180°＝(180°－∠AOB)，

解得∠AOB＝108°.

2、如图，梯形ABCD中，AD∥BC，∠ABC＝90°，AD＝2，AB＝1，BC＝3.若此梯形的顶点A，B恰好在圆O的直径MN上，C，D在圆O上，则圆O的直径等于__2__．

【思路生成】首先连结OC，OD，然后设OC＝OD＝x，OB＝y，由在Rt△OAD中，OA2＋AD2＝OD2，在Rt△OBC中，OB2＋BC2＝OC2，可得方程组即可求得圆O的直径．

答图[来源:学科网]

【解析】 如答图，连结OC，OD，∵梯形ABCD中，AD∥BC，∠ABC＝90°，∴∠OAD＝90°，∠OBC＝90°，设OC＝OD＝x，OB＝y，在Rt△OAD中，OA2＋AD2＝OD2，在Rt△OBC中，OB2＋BC2＝OC2，∵AD＝2，AB＝1，BC＝3，∴解得∴圆O的直径等于2.

二、垂径定理

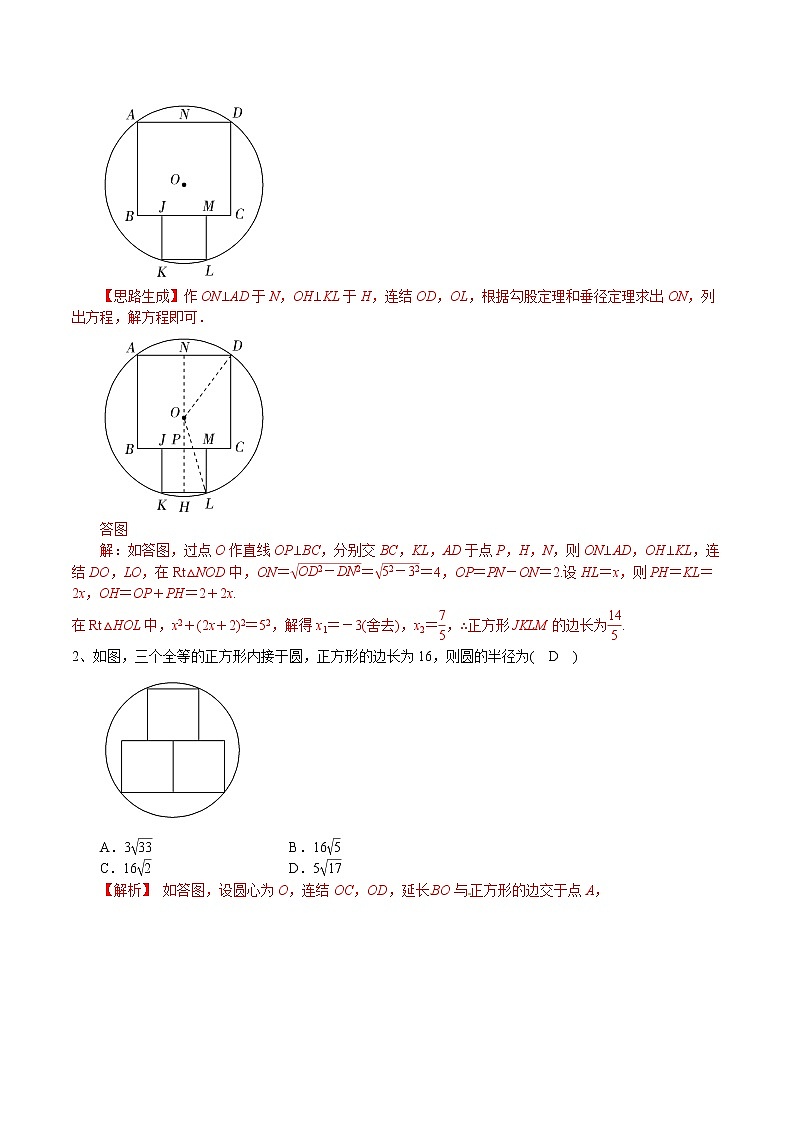
1、如图，正方形ABCD的顶点A，D和正方形JKLM的顶点K，L在一个以5为半径的圆O上，点J，M在线段BC上，若正方形ABCD的边长为6，求正方形JKLM的边长．

【思路生成】作ON⊥AD于N，OH⊥KL于H，连结OD，OL，根据勾股定理和垂径定理求出ON，列出方程，解方程即可．

答图

解：如答图，过点O作直线OP⊥BC，分别交BC，KL，AD于点P，H，N，则ON⊥AD，OH⊥KL，连结DO，LO，在Rt△NOD中，ON＝＝＝4，OP＝PN－ON＝2.设HL＝x，则PH＝KL＝2x，OH＝OP＋PH＝2＋2x.

在Rt△HOL中，x2＋(2x＋2)2＝52，解得x1＝－3(舍去)，x2＝，∴正方形JKLM的边长为.

2、如图，三个全等的正方形内接于圆，正方形的边长为16，则圆的半径为(　D　)

[来源:Z§xx§k.Com]

A．3  B．16

C．16  D．5

【解析】 如答图，设圆心为O，连结OC，OD，延长BO与正方形的边交于点A，

答图

设圆心与上面正方形的距离为x，则BO＝16－x，AD＝8，AO＝16＋x，

在Rt△OBC与Rt△OAD中，

∵OC＝OD，

∴BC2＋OB2＝AO2＋AD2，[来源:学&科&网]

即162＋(16－x)2＝(16＋x)2＋82，

解得x＝3，∴OB＝16－3＝13，

∴OC＝＝＝5.

3、(1)如图1，多边形ABDEC是由边长为2的等边三角形ABC和正方形BDEC组成，⊙O过点A，D，E三点，求⊙O的半径；

(2)如图2，若多边形ABDEC是由一个等腰三角形和一个矩形组成，AB＝AC＝BD＝2，⊙O过A，D，E三点，则⊙O的半径是否改变？

答图

解：(1)如答图，过A作BC的垂线交DE于F点，

∵△ABC为等边三角形，∴AF平分BC，

∵四边形BDEC为正方形，∴AF也垂直平分DE，

∴过点A，D，E三点的圆的圆心O在AF上，

连结AD，OD，则OA＝OD，∴∠OAD＝∠ODA，

又∵BC＝BD＝BA，∴∠BAD＝∠BDA，

而AF∥BD，∴∠OAD＝∠BDA，

∴∠ODA＝∠BAD，∴AB∥OD，∴四边形ABDO为菱形，

∴AO＝AB＝2，即⊙O的半径为2；

(2)⊙O的半径不改变．

因为AB＝AC＝BD＝2，此题的求法和(1)一样，⊙O的半径为2.

三、垂径定理的应用

1、如图，半径为2的圆O中，弦AB与弦CD垂直相交于P，连结OP，若OP＝1，求AB2＋CD2的值．

【思路生成】解互相垂直的两条弦问题，常需多次运用垂径定理．

解：如答图，过O点作OE⊥AB于E，OF⊥CD于F，

连结OD，OA，则AE＝BE，CF＝DF.

答图

∵OE2＝AO2－AE2＝4－AB2，OF2＝OD2－FD2＝4－CD2，∴OE2＋OF2＝＋＝PF2＋OF2＝OP2＝12，

即4－AB2＋4－CD2＝1，故AB2＋CD2＝28.

2、如图，圆O中，弦AC⊥BD，且OE⊥CD于E，若AB的长是10，则OE的长是__5__．

         答图

【解析】 如答图，作直径DF，连结CF，则∠DCF＝90°，∠1＋∠2＝90°，

∵AC⊥BD，∴∠3＋∠4＝90°，

∵∠2＝∠4，∴∠1＝∠3，∴＝，

∴AB＝CF＝10.∴OE⊥CD于点E，∴CE＝DE.

∵OD＝OF，∴OE＝CF＝5.

3、如图，圆O中两条互相垂直的弦AB和CD的弦心距是3和2，它们将圆O分成四部分：S1，S2，S3，S4，求(S1＋S3)－(S2＋S4)．

解：如答图，以O为对称中心，在⊙O内分别作与AB，CD对称的弦A′B′，C′D′.

观察此图，由题设条件，及圆的对称性可知(S1＋S3)－(S2＋S4)＝阴影长方形的面积＝4×6＝24.

答图[来源:学*科*网Z*X*X*K]

四、圆心角定理

1、如图，已知⊙O的半径为R，C，D是直径AB同侧圆周上的两点，的度数为96°，的度数为36°，动点P在AB上，则CP＋PD的最小值为__R__．

【解析】 如答图，作点D关于AB的对称点D′，连结CD′，

由轴对称确定最短路线问题，CD′与AB的交点即为所求的点P，CD′的长度为PC＋PD的最小长度，

答图[来源:Z.xx.k.Com]

∵度数为96°，∴的度数为180°－96°＝84°，

连结OD′，∵＝36°，∴＝36°，

∴＝84°＋36°＝120°，即∠COD′＝120°，

过点O作OE⊥CD′，则∠COE＝∠COD′＝60°，OE垂直平分CD′，∴CD′＝2CE＝2×R＝R，即CP＋PD的最小值为R.

1、如图，在三个等圆上各自有一条劣弧AB，CD，EF，如果＋＝，那么AB＋CD与EF的大小关系是(　C　)

A．AB＋CD＝EF  B．AB＋CD<EF

C．AB＋CD>EF  D．大小关系不确定

【解析】 如答图，在上取一点M使＝，则＝，∴AB＝FM，CD＝EM，在△MEF中，FM＋EM>EF，∴AB＋CD>EF.

答图