专题19 以形助数“数题形解”-备战2022高考数学冲破压轴题讲与练

专题19   以形助数“数题形解”

【压轴综述】

1．数形结合的数学思想：包含“以形助数”和“以数辅形”两个方面，其应用大致可以分为两种情形：一是借助形的生动性和直观性来阐明数之间的联系，即以形作为手段，数作为目的，比如应用函数的图象来直观地说明函数的性质；二是借助于数的精确性和规范严密性来阐明形的某些属性，即以数作为手段，形作为目的，如应用曲线的方程来精确地阐明曲线的几何性质．

2．运用数形结合思想分析解决问题时，要遵循三个原则：

（1）等价性原则．在数形结合时，代数性质和几何性质的转换必须是等价的，否则解题将会出现漏洞．有时，由于图形的局限性，不能完整的表现数的一般性，这时图形的性质只能是一种直观而浅显的说明，要注意其带来的负面效应．

（2）双方性原则．既要进行几何直观分析，又要进行相应的代数抽象探求，仅对代数问题进行几何分析容易出错．

（3）简单性原则．不要为了“数形结合”而数形结合．具体运用时，一要考虑是否可行和是否有利；二要选择好突破口，恰当设参、用参、建立关系、做好转化；三要挖掘隐含条件，准确界定参变量的取值范围，特别是运用函数图象时应设法选择动直线与定二次曲线．

3．数形结合思想是解答高考数学试题的一种常用方法与技巧，特别是在解选择题、填空题时发挥着奇特功效，这就要求我们在平时学习中加强这方面的训练，以提高解题能力和速度．具体操作时，应注意以下几点：

（1）准确画出函数图象，注意函数的定义域；

（2）用图象法讨论方程（特别是含参数的方程）的解的个数是一种行之有效的方法，值得注意的是首先要把方程两边的代数式看作是两个函数的表达式（有时可能先作适当调整，以便于作图），然后作出两个函数的图象，由图求解；

（3）在解答题中数形结合思想是探究解题的思路时使用的，不可使用形的直观代替相关的计算和推理论证．

本专题通过例题重点说明说明“以形助数，数题形解”这类问题的方法与技巧.

【压轴典例】

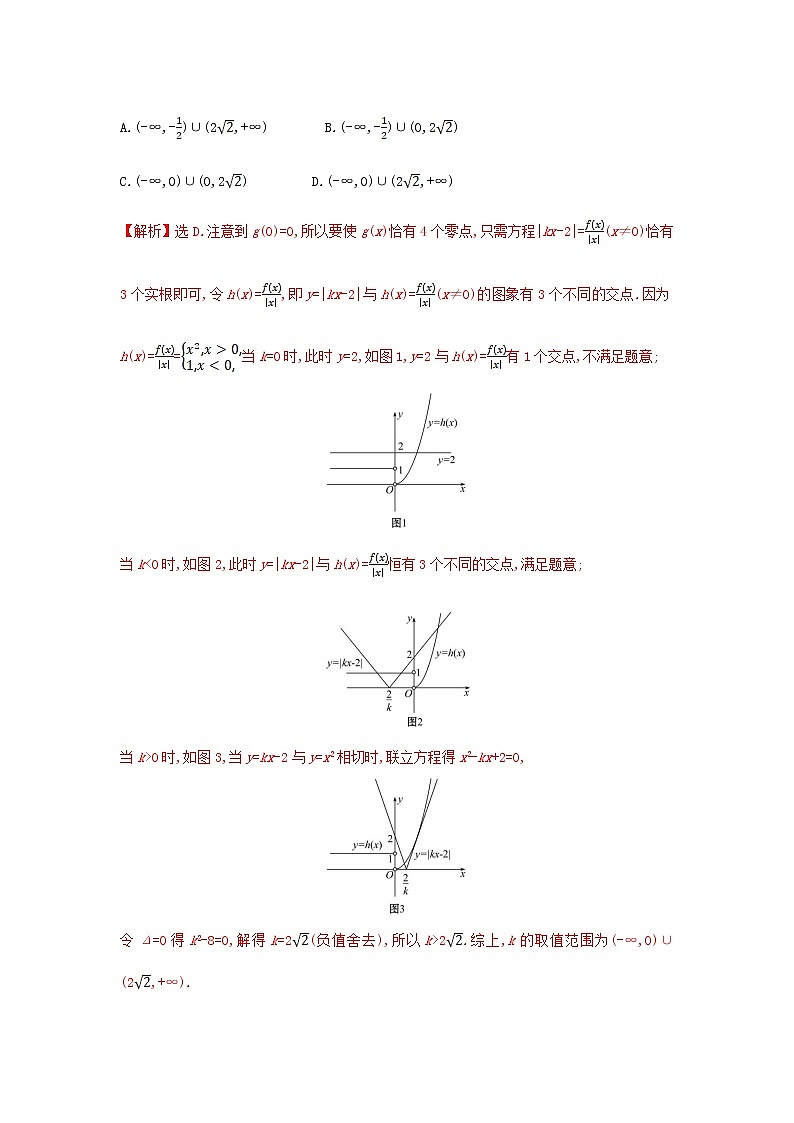
例1.(2020·天津高考·T9)已知函数f(x)=若函数g(x)=f(x)-(k∈R)恰有4个零点,则k的取值范围是              (　　)

A.(-∞,-)∪(2,+∞)        B.(-∞,-)∪(0,2)

C.(-∞,0)∪(0,2)         D.(-∞,0)∪(2,+∞)

例2.(2020·全国卷Ⅲ文科·T6)在平面内,A,B是两个定点,C是动点.若·=1,则点C的轨迹为              (　　)

A.圆 B.椭圆 C.抛物线 D.直线

例3.(2020·新高考全国Ⅰ卷)已知P是边长为2的正六边形ABCDEF内的一点,则·的取值范围是              (　　)

A.(-2,6) B.(-6,2)  C.(-2,4)  D.(-4,6)

例4．（2021·陕西西安市西光中学）已知点在抛物线上，是抛物线的焦点，点为直线上的动点，我们可以通过找对称点的方法求解两条线段之和的最小值，则的最小值为（    ）

A．8 B． C． D．

例5．（2021·四川遂宁市·高三）古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名．他发现：平面内到两个定点的距离之比为定值的点所形成的图形是圆．后来，人们将这个圆以他的名字命名，称为阿波罗尼斯圆，简称阿氏圆．已知在平面直角坐标系中，，，点满足．当三点不共线时，面积的最大值为（    ）

A．24 B．12 C． D．

例6．（2020·天津南开区·南开中学高三）菱形的边长为6，，如果点是菱形内一点，且，则线段的长为（    ）

A． B． C．或 D．或

例7.(2020·浙江高考·T15)设直线l:y=kx+b(k>0),圆C1:x2+y2=1,C2:(x-4)2+y2=1,若直线l与C1,C2都相切,则k=　　　　;b=　　　　. 

例8.(2020·江苏高考·T14)在平面直角坐标系xOy中,已知P,A,B是圆C:x2+=36上的两个动点,满足PA=PB,则△PAB面积的最大值是　　　　. 

例9．（2020·浙江大学附属中学高三）已知正项数列满足，则下列正确的是（    ）

A．当时，递增，递增

B．当时，递增，递减

C．当时，递增，递减

D．当时，递减，递减

例10.(2020·全国卷Ⅲ文科·T21理科·T20)(12分)已知椭圆+=1(0<m<5)的离心率为,A,B分别为C的左、右顶点.

(1)求C的方程;

(2)若点P在C上,点Q在直线x=6上,且=,BP⊥BQ,求△APQ的面积.

【压轴训练】

1.（浙江省金华十校2020届高三）已知向量，满足：，，，且，则的最小值为　　

A．    B．4    C．    D．

2. （2020江苏扬州中学高三）已知椭圆的左、右焦点分别为，，为椭圆上不与左右顶点重合的任意一点，，分别为的内心和重心，当轴时，椭圆的离心率为（   ）

A． B． C． D．

3.（福建省福州市2020高三）如图，函数的图像为两条射线，组成的折线，如果不等式的解集中有且仅有1个整数，那么实数的取值范围是（    ）

A．    B．

C．    D．

4.（2020·四川重庆高三）过曲线的左焦点作曲线的切线，设切点为延长交曲线于点其中有一个共同的焦点，若则曲线的离心率为（    ）．

A． B． C． D．

5．（2020·江苏启东中学）设是椭圆上一点，分别是两圆和上的点，则的最小值和最大值分别为（   ）

A．4，8 B．2，6 C．6，8 D．8，12

6.【 2020云南省昆明市第一中学高三】已知函数，若两个正数，满足，则的取值范围是（    ）

A.     B.     C.     D.

7．（2020·福清西山学校高三）设函数，已知在有且仅有个极小值点，有下述四个结论：其中所有正确结论的编号是（    ）

①在有且仅有个零点；②在有且仅有个极大值点；③在单调递减；④的取值范围是.

A．①④ B．②③ C．②④ D．③④

8．（2020·江苏星海实验中学）已知任意实数，关于的不等式恒成立，则实数的最大整数值为（    ）

A． B． C． D．

9. （2020浙江省金丽衢十二校2019高三）定义在上的偶函数满足：当时有，且当时，，若方程恰有三个实根，则的取值范围是____．

10.（2018·上海华师大二附中）已知，当取得最小值时，曲线上的点到直线的距离的取值范围是_________.

11．（2021·广西梧州市·高三）已知点，抛物线：（）的准线为，点在上，作于点，，，则___________.

12．（2021·江西鹰潭市·高三）方程表示的曲线为函数的图象.对于函数，现有如下结论：①函数的值域是R；②在R上单调递减；③的图象不经过第三象限；④直线与曲线没有交点.其中正确的结论是___________.

13．（2020·广州市天河中学高三）已知椭圆的上焦点为，是椭圆上一点，点，当点 在椭圆上运动时，的最大值为__________.

14．（2021·浙江高三开学考试）如图，已知过拋物线的焦点的直线交抛物线于点点在第一象限)，线段的中点为拋物线在点处的切线与以为直径的圆交于另一点.

（1）若，求直线的方程；

（2）试问是否为定值？若是，请求出该定值；若不是，请求出它的最大值.

15．（2020·长沙市·湖南师大附中高三）在平面直角坐标系中，已知椭圆的左､右焦点分别为，，离心率为，过的直线与椭圆C交于P，Q两点，若的周长为8.

（1）求椭圆C的方程；

（2）动直线交椭圆于，两点，交轴于点．点是关于的对称点，的半径为．设为的中点，，与分别相切于点，，求的最小值.