【2022高考必备】2012-2021十年全国高考数学真题分类汇编（文科） 立体几何大题（精解精析）

2012-2021十年全国高考数学真题分类汇编  （文科）

立体几何大题（原卷版）

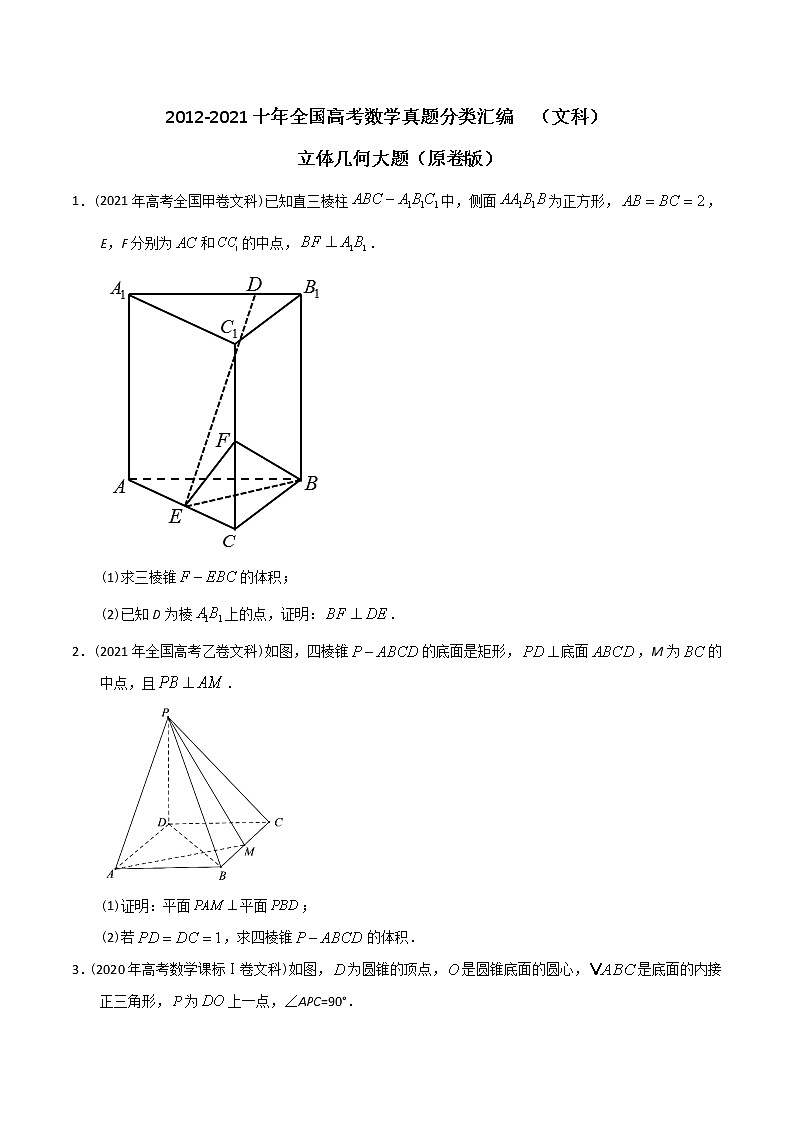
1．(2021年高考全国甲卷文科)已知直三棱柱中，侧面为正方形，，E，F分别为和的中点，．

(1)求三棱锥的体积；

(2)已知D为棱上的点，证明：．

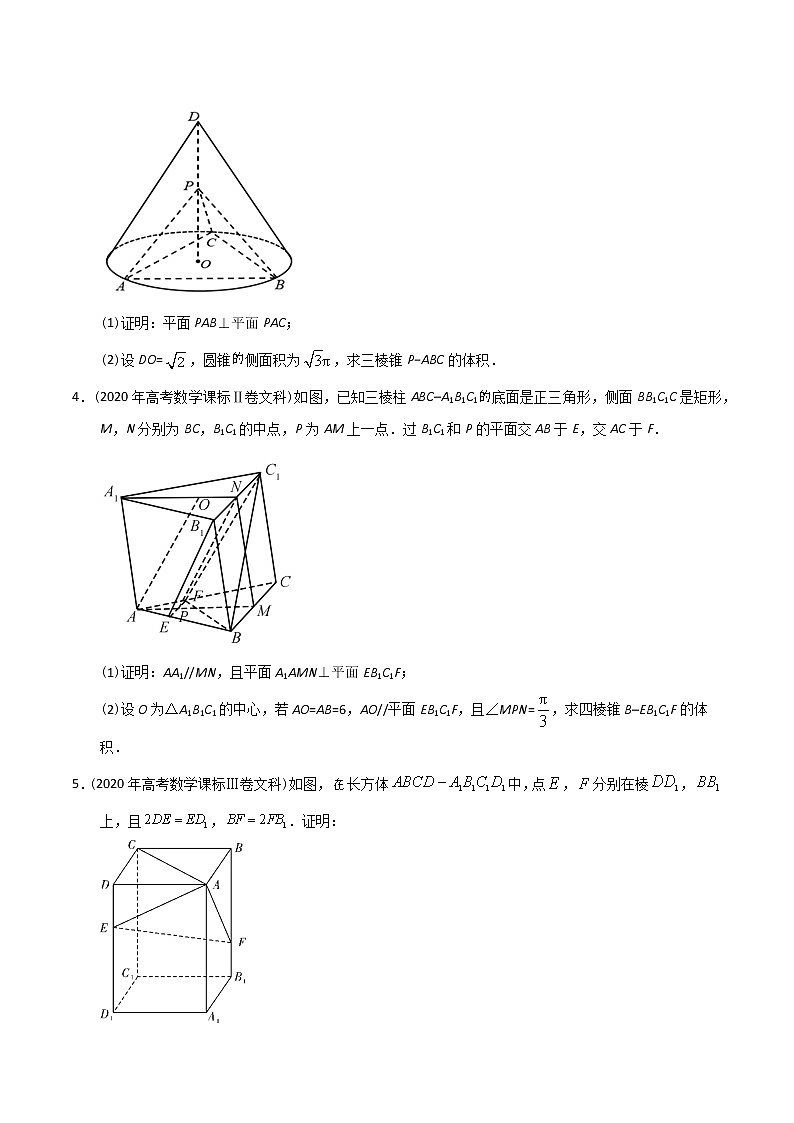
2．(2021年全国高考乙卷文科)如图，四棱锥的底面是矩形，底面，M为的中点，且．

(1)证明：平面平面；

(2)若，求四棱锥的体积．

3．(2020年高考数学课标Ⅰ卷文科)如图，为圆锥的顶点，是圆锥底面的圆心，是底面的内接正三角形，为上一点，∠APC=90°．

(1)证明：平面PAB⊥平面PAC；

(2)设DO=，圆锥侧面积为，求三棱锥P−ABC的体积．

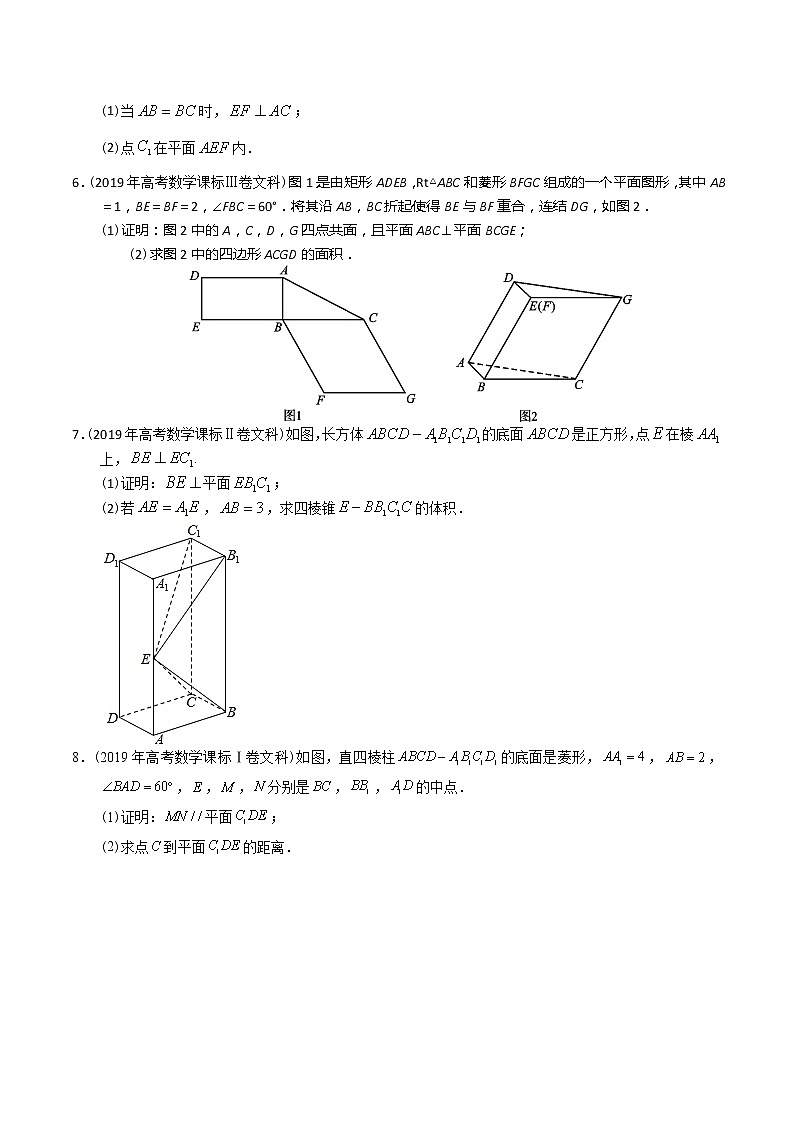
4．(2020年高考数学课标Ⅱ卷文科)如图，已知三棱柱ABC–A1B1C1底面是正三角形，侧面BB1C1C是矩形，M，N分别为BC，B1C1的中点，P为AM上一点．过B1C1和P的平面交AB于E，交AC于F．

(1)证明：AA1//MN，且平面A1AMN⊥平面EB1C1F；

(2)设O为△A1B1C1的中心，若AO=AB=6，AO//平面EB1C1F，且∠MPN=，求四棱锥B–EB1C1F的体积．

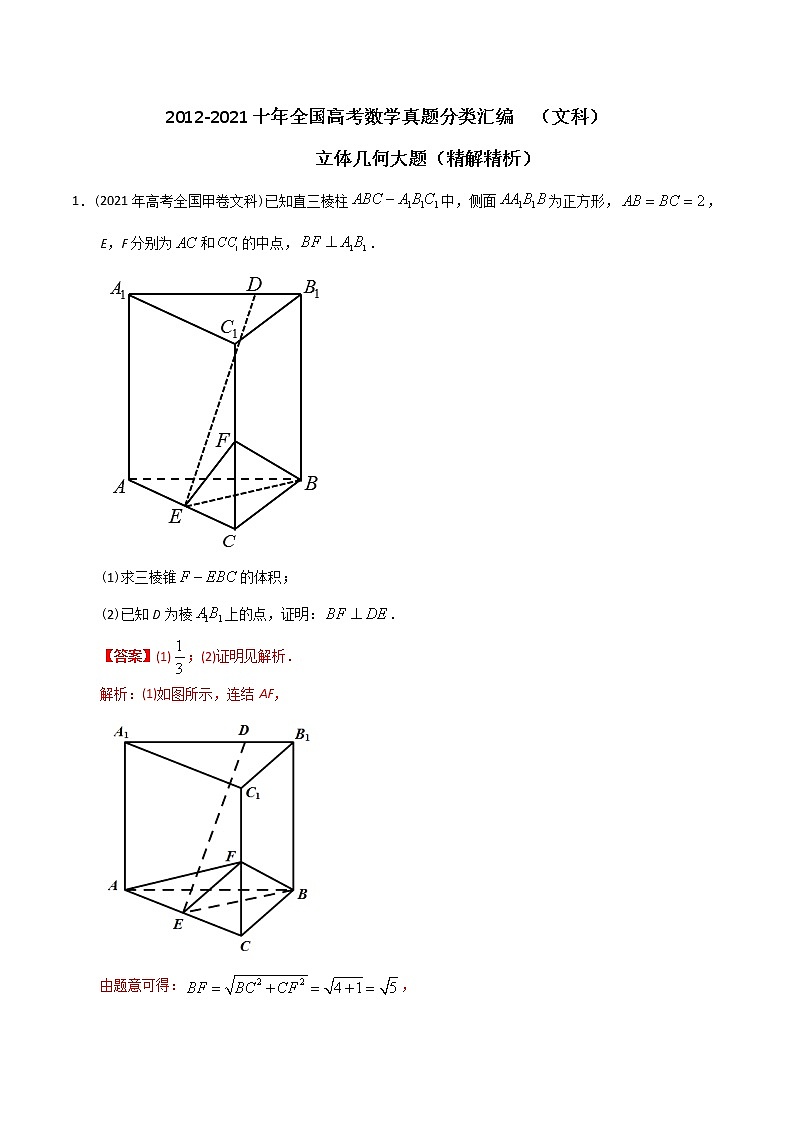
5．(2020年高考数学课标Ⅲ卷文科)如图，长方体中，点，分别在棱，上，且，．证明：

(1)当时，；

(2)点在平面内．

6．(2019年高考数学课标Ⅲ卷文科)图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB＝1，BE＝BF＝2，∠FBC＝60°．将其沿AB，BC折起使得BE与BF重合，连结DG，如图2．

(1)证明：图2中的A，C，D，G四点共面，且平面ABC⊥平面BCGE；

(2)求图2中的四边形ACGD的面积．

7．(2019年高考数学课标Ⅱ卷文科)如图，长方体的底面是正方形，点在棱上，

(1)证明：平面；

(2)若，，求四棱锥的体积．

8．(2019年高考数学课标Ⅰ卷文科)如图，直四棱柱的底面是菱形，，，，，，分别是，，的中点．

(1)证明：平面；

(2)求点到平面的距离．

9．(2018年高考数学课标Ⅲ卷文科)(12分)如图，矩形所在平面与半圆弧所在平面垂直，是上异于，的点．

(1)证明：平面平面；

(2)在线段上是否存在点，使得平面？说明理由．

10．(2018年高考数学课标Ⅱ卷文科)(12分)如图，在三棱锥中，，，为的中点．

(1)证明：平面；

(2)若点在棱上，且，求点到平面的距离．

11．(2018年高考数学课标Ⅰ卷文科)(12分)如图，在平行四边形中，，． 以为折痕将折起，使点到达点D的位置，且．

(1)证明：平面平面；

(2)为线段上一点，为线段上一点，且，求三棱锥的体积．

12．(2017年高考数学课标Ⅲ卷文科)如图,四面体中,是正三角形,．

(1)证明:;

(2)已知是直角三角形,．若为棱上与不重合的点,且,求四面体与四面体的体积比．

13．(2017年高考数学课标Ⅱ卷文科)如图,四棱锥中,侧面为等边三角形且垂直于底面,,

(1)证明:直线∥平面;

(2)若△面积为,求四棱锥的体积．

14．(2017年高考数学课标Ⅰ卷文科)如图,在四棱锥中,,且．

(1)证明:平面平面;

(2)若,且四棱锥的体积为,求该四棱锥的侧面积．

15．(2016年高考数学课标Ⅲ卷文科)(本小题满分12分)如图，四棱锥中，底面，，，，为线段上一点，，为的中点．

(Ⅰ)证明平面;

(Ⅱ)求四面体的体积．

16．(2016年高考数学课标Ⅱ卷文科)(本小题满分12分)如图，菱形的对角线与交于点，点分别在上，，交于点．将沿折到的位置．

(1)证明：；

(2)若，求五棱锥体积．

17．(2016年高考数学课标Ⅰ卷文科)(本题满分12分)如图，在已知正三棱锥P-ABC的侧面是直角三角形，PA=6，顶点P在平面ABC内的正投影为点D，D在平面PAB内的正投影为点E，连接PE并延长交AB于点G．

(I)证明G是AB的中点；

(II)在图中作出点E在平面PAC内的正投影F(说明作法及理由)，并求四面体PDEF的体积．

18．(2015年高考数学课标Ⅱ卷文科)(本小题满分12分)如图,长方体中，点分别在上,过点的平面与此长方体的面相交,交线围成一个正方形．

(Ⅰ)在图中画出这个正方形(不必说明画法与理由)；

(Ⅱ)求平面把该长方体分成的两部分体积的比值．

19．(2015年高考数学课标Ⅰ卷文科)(本小题满分12分)如图四边形ABCD 为菱形，为与交点，，

(I)证明：平面平面；

(II)若， 三棱锥的体积为，求该三棱锥的侧面积．

20．(2014年高考数学课标Ⅱ卷文科)如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．

(Ⅰ)证明：PB∥平面AEC；

(Ⅱ)设AP=1，AD=，三棱锥P-ABD的体积，求A到平面PBC的距离．

21．(2014年高考数学课标Ⅰ卷文科)如图，三棱柱中，侧面为菱形，的中点为，且平面．

(1)证明：

(2)若,求三棱柱的高．

22．(2013年高考数学课标Ⅱ卷文科)如图，直三棱柱中，，分别是，的中点．

(Ⅰ)证明：平面；

(Ⅱ)设，，求三棱锥的体积．

23．(2013年高考数学课标Ⅰ卷文科)如图，三棱柱中，，，．

(1)证明：；

(2)若，，求三棱柱的体积．

24．(2012年高考数学课标卷文科)如图，三棱柱中，侧棱垂直底面，，，D是棱AA1的中点

(1)证明：平面⊥平面；

(2)平面分此棱柱为两部分，求这两部分体积的比．