专题13三角函数与解三角形A辑-2022年高考数学压轴必刷题（第二辑）

2022年高考数学压轴必刷题（第二辑）

专题13三角函数与解三角形A辑

1．若、是小于180的正整数，且满足.则满足条件的数对共有（    ）

A．2对 B．6对 C．8对 D．12对

【答案】A

解：、，所以，，结合观察正弦函数的图像，

满足的只可能以下两种情况：

（1）时，

或，

所以或.

（2）时，同样有，此时，但，

则，所以此时没有满足题意的整数对；

综合（1）（2），满足题意的有2对.

故选：A

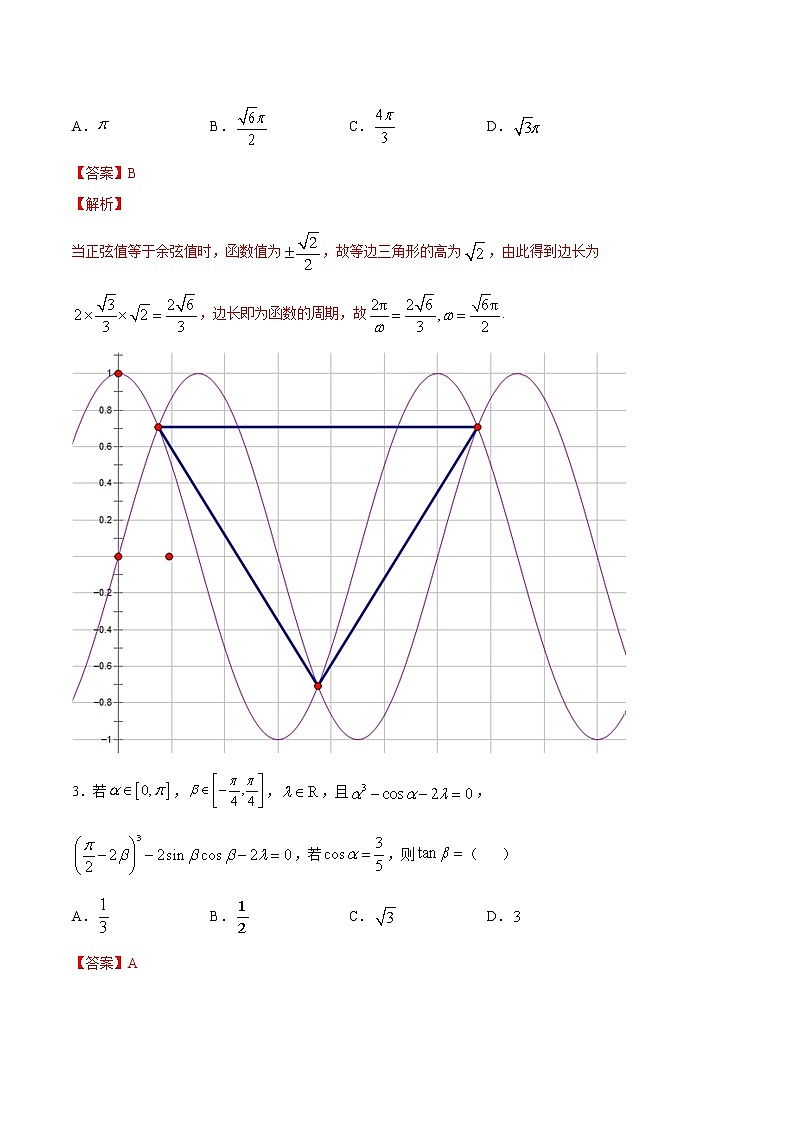
2．已知，顺次连接函数与的任意三个相邻的交点都构成一个等边三角形，则（    ）

A． B． C． D．

【答案】B

【解析】

当正弦值等于余弦值时，函数值为，故等边三角形的高为，由此得到边长为，边长即为函数的周期，故.

3．若，，，且，，若，则（    ）

A． B． C． D．

【答案】A

由得

即，

设，因为，，

所以在上单调递增，

由，即，

，即.

所以，由在上单调递增.

由，，则，可得，

∴，∴，∴，

由，，所以

∴，∴.

故选：A

4．已知锐角的内角，，的对边分别为，，，若，，则面积的取值范围是（    ）

A． B． C． D．

【答案】A

【解析】

因为,,，所以 ， , 由正弦定理得，可化简为 ，由 得 从而得 ， ，故选A.

5．锐角的内角，，的对边分别为，，且，，若，变化时，存在最大值，则正数的取值范围是（    ）

A． B． C． D．

【答案】A

解：因为，，所以，

可得：，即，

因为为锐角三角形，则有，即，解得：.

= ，

当时，原式有最大值，此时，

则，，，即，所以.

故选：A.

6．在中，内角A，B，C的对边分别是a，b，c，，，点D在边上，且，则线段长度的最小值为（    ）

A． B． C．3 D．2

【答案】A

由及正弦定理，得，即，

由余弦定理得，，∵，∴.

由于，∴，两边平方，得

，当且仅当时取等号，

即，∴线段长度的最小值为.

故选：A.

7．定义在区间的函数有（    ）个零点？（其中表示不大于实数x的最大整数）

A．2 B．3 C．4 D．5

【答案】D

令，则，

，则问题转化为求的根的个数.

分别作出和的图象，如图所示：

则有或或，即或或.

或或，

或或.

或或或或.

∴函数有5个零点.

故选：D.

8．设函数，则下列结论正确的个数是（    ）

①当时，的最小正周期为；

②当时，的最大值为；

③当时，的最大值为．

A．0 B．1 C．2 D．3

【答案】C

①当时，，的最小正周期为，故①正确；

②因为，故②正确；

③当时，设，，

令，，，

且当时，取得极小值，

极小值为．

令，解得．

（ⅰ）当时，在内无极值点，

，，，所以的最大值为．

（ⅱ）当时，由，

知．又，

所以的最大值为，故③错误．

故选：C.

9．已知函数，则f（x）的最小值为（    ）

A． B． C． D．

【答案】C

令为减函数，且

所以当时，，从而，

当时，，从而，

故.

故选：C.

10．已知函数的最小正周期为，其图象关于直线对称．给出下面四个结论：①将的图象向右平移个单位长度后得到函数图象关于原点对称；②点为图象的一个对称中心；③；④在区间上单调递增．其中正确的结论为（    ）

A．①② B．②③ C．②④ D．①④

【答案】C

因为函数的最小正周期为，其图象关于直线对称，

所以 ，解得，

因为，所以，因此，

①将的图象向右平移个单位长度后函数解析式为，

由，得，所以其对称中心为：，故①错；

②由，解得，即函数的对称中心为；令，则，故②正确；

③由，故③错；

④由，得，

即函数的增区间为，因此在区间上单调递增，故④正确.

故选：C.

11．将函数的图象向右平移个单位后得到函数的图象，若函数在区间和上均单调递增，则实数a的取值范围是（    ）

A． B． C． D．

【答案】A

根据题意，将函数的图象向右平移个单位后得到函数的图象，则

.

根据函数的单调增区间满足，解得.

当时，函数的增区间为，当时，函数的增区间为.

若满足函数在区间和上均单调递增，则

，解得.

故选：A.

12．已知正实数，设，.若以为某个三角形的两边长，设其第三条边长为，且满足，则实数的取值范围为（    ）

A． B． C． D．

【答案】D

解：先根据基本不等式得：，，

因为其第三条边长为，且满足，

所以由余弦定理得：，

因为

所以，即，

所以.

故选：D.

13．已知函数图象关于直线对称，由此条件给出5个结论：①的值域为；②图像关于点对称；③的图像向右平移后可得到；④在区间上单调递减；⑤且．则上述所有结论中正确的编号是（    ）

A．①②③④ B．①③④⑤ C．②③⑤ D．③④⑤

【答案】A

因为，

又由图象关于直线对称，则有，解得，

即函数，

进而的值域为，故序号①正确，而序号⑤错误；

令，，得，

显然函数关于点对称，但为其中一个对称点，故序号②正确；将函数图像向右平移后，

得，于是序号③正确；

易知在区间单调递减，即序号④正确，

综上可得，正确序号为①②③④.

故选：A．

14．给定下列4个独立编号的命题：

①设，，且，则二元函数的最小值为20

②已知，函数在上是增函数，则的最大值为3

③在中，为中点，，在线段上，则的最小值为

④若，，则，，则．

请你根据逻辑推理相关知识，那么上述所有命题中不成立的编号是（    ）

A．①② B．②③ C．③④ D．①④

【答案】C

对于序号①：∵，，且，则，∴二元函数可化为

，故序号①正确；

对于序号②：∵，函数在上是增函数，即，使在上是增函数，则，显然，而，

于是，故的最大值为3．∴序号②正确．

对于序号③：由已知条件，∵，当且仅当时取等号，故序号③错误．

对于序号④：∵，∴，由于，则，

又，则，由于，于是．而，故序号④错误，综上知，不成立的序号为③④，而正确的序号为①②．

故选：C．

15．△ABC中，BD是AC边上的高，A=，cosB=-，则=（　　）

A． B． C． D．

【答案】A

解：

由正弦定理可知

，即   

故选A．

16．已知函数在区间上有且仅有2个零点，对于下列4个结论：①在区间上存在，满足；②在区间有且仅有1个最大值点；③在区间上单调递增；④的取值范围是，其中所有正确结论的编号是(    )

A．①③ B．①③④ C．②③ D．①④

【答案】B

，

，

令，则，

由题意在上只能有两解和，

，（*）

因为上必有，

故在上存在满足，①成立；

开对应的（显然在上）一定是最大值点，

因对应的值有可能在上，故②结论错误；

解（*）得，所以④成立；

当时，，

由于，

故，

此时是增函数，从而在上单调递增. 所以③成立

综上，①③④成立，

故选：B.

17．函数的部分图象如图中实线所示，图中圆与的图象交于，两点，且在轴上，下列说法：①函数的最小正周期是；②函数的图象关于点成中心对称；③点的坐标是，其中正确结论的个数是（    ）

A．0 B．1 C．2 D．3

【答案】B

①中，根据函数的图象以及圆的对称性，

可得，两点关于圆心对称，所以，

于是，所以，解得，函数的周期为，所以①错误；

②中，由函数图象关于点对称，及周期知，

函数图象的对称中心为，

而不存在的解，所以②错误；

③中，由及的相位为0，得，

所以，，从而，所以③正确.

故选：B.

18．若面积为1的满足，则边的最小值为（    ）

A．1 B． C． D．2

【答案】C

解：的面积，且，

，

，

根据余弦定理得：

，

即，

可得，

，

则，

解得：，

即边的最小值为.

故选：C.

19．若不等式，对于成立，则，分别等于（    ）

A．； B．； C．； D．；

【答案】D

由，则，

当或时，即或时，，

当时，即时，，

所以当或时，，

当时，，

设函数，则在上单调递增，在上单调递减，

且函数的图象关于直线对称，所以，

所以，解得，

又由，解得，

所以，.

故选：D.

A．①② B．②③④ C．①③④ D．①②④

【答案】D

函数，函数的定义域为，

，

所以函数为奇函数．故①正确．

，所以函数的最小值正周期为，故函数为周期函数，故②正确．

当时，，，不对；故③错误；

由在单调递增，而在单调递减，可知在单调递增，

函数在单调递增，根据①可知是奇函数，在区间，单调递增，

则在区间内单调递增；故④正确；

故选：．

21．平面四边形为凸四边形，且，，，，则的取值范围为（    ）

A． B． C． D．

【答案】D

设，在中，，所以，解得，

延长交于点，则由得，，

若，则，

显然点在线段（不含端点）上，所以的取值范围是．

故选：D．

22．已知的三个内角所对的边分别为，满足，且，则的形状为（   ）

A．等边三角形 B．等腰直角三角形

C．顶角为的等腰三角形 D．顶角为的等腰三角形

【答案】D

由题

即，由正弦定理及余弦定理得

即

故 整理得 ，故

故为顶角为的等腰三角形

故选D

23．在中，内角，，的对边分别为，，，其中为钝角，且满足，，若点与点在的两侧，且，，，四点共圆，则四边形面积的最大值为（    ）

A． B． C． D．

【答案】C

由,得,由正弦定理得

,又为钝角,,又四点共圆

,在中,由余弦定理得:

即，当且仅当时,等号成立.

同理,在中，，即，,

四边形面积的最大值为.

故选:.

24．函数的图像向左平移个单位长度后对应的函数是奇函数，函数．若关于的方程在内有两个不同的解，则的值为（     ）

A． B． C． D．

【答案】D

函数的图像向左平移个单位长度后，可得的图象.

由条件为奇函数，则，即

又，所以，即

关于的方程在内有两个不同的解，

即在内有两个不同的解，

即在内有两个不同的解，

即，其中(为锐角) 在内有两个不同的解，

即方程即在内有两个不同的解，

由，则，

所以，

所以

则，即，

所以，

故选：D

25．设中角，，所对的边分别为，，，下列式子一定成立的是（    ）．

A．

B．

C．．

D．

【答案】C

对A，令，可判断等式不成立，故A错误；

对B,由余弦定理可得，故B错误；

对于C选项，由可得，

即，

整理得，移项可得C选项，故C正确；

对于D选项，由，有，，而，

可得，故D错误，

故选：C．

26．已知中，的对边长度分别为，已知点为该三角形的外接圆圆心，点分别为边的中点，则（   ）

A． B． C． D．

【答案】D

如图：


在三角形中，AB=c,BC=a,AC=b.
，
同理，
所以

=：：，

由正弦定理，可得=，

故选：D.

27．若直线与函数的图象相交于点，，且，则线段与函数的图象所围成的图形面积是

A． B． C． D．

【答案】A

【解析】

线段与函数的图象所围成的图形面积如图阴影部分所示，其面积为 ，选A

28．已知，现将函数的图象向右平移个单位后得到函数的图象，若两函数与图象的对称中心完全相同，则满足题意的的个数为（    ）

A．1 B．2

C．3 D．4

【答案】B

依题化简得：，根据正余弦曲线与正切曲线的图象性质，欲使得两函数图象对称中心一致，须为奇函数，且只能为，有如图的两类情况．

29．已知三角形的三边长是公差为2的等差数列，且最大角的正弦值为，则这个三角形的周长是（   ）

A．18 B．15 C．21 D．24

【答案】B

根据题意设△ABC的三边长分别为a，a+2，a+4，且a+4所对的角为最大角α，

∵sinα，∴cosα或，

当cosα时，α＝60°，不合题意，舍去；

当cosα时，α＝120°，由余弦定理得：cosα＝cos120°，

解得：a＝3或a＝﹣2（不合题意，舍去），

则这个三角形周长为a+a+2+a+4＝3a+6＝9+6＝15．

故选B．

30．已知函数有且只有三个零点，则属于(    )

A． B． C． D．

【答案】D

由已知，有且仅有三个不同零点等价于方程有且仅有三个

不同实根，等价于与有且仅有三个不同交点，

如图

当与相切时，满足题意，因为，

所以，且，消a得

由诱导公式，有，

又，所以.

故选：D