
初中数学浙教版九年级下册3.2 简单几何体的三视图课堂检测
展开3.2简单几何体的三视图
班级: 姓名:
一、单选题
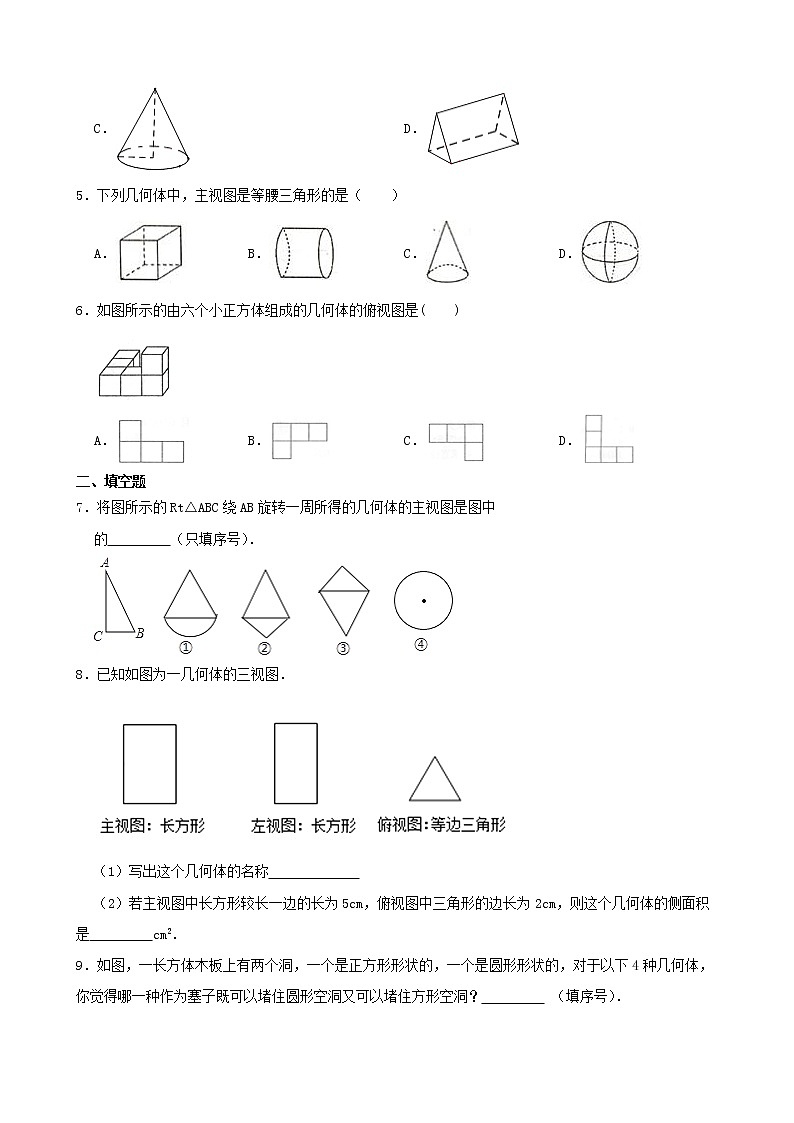
1.如图,一个放置在水平桌面上的圆柱,它的主(正)视图是( )
A.B.C.D.
【答案】C
【解析】解:圆柱的主(正)视图为矩形.
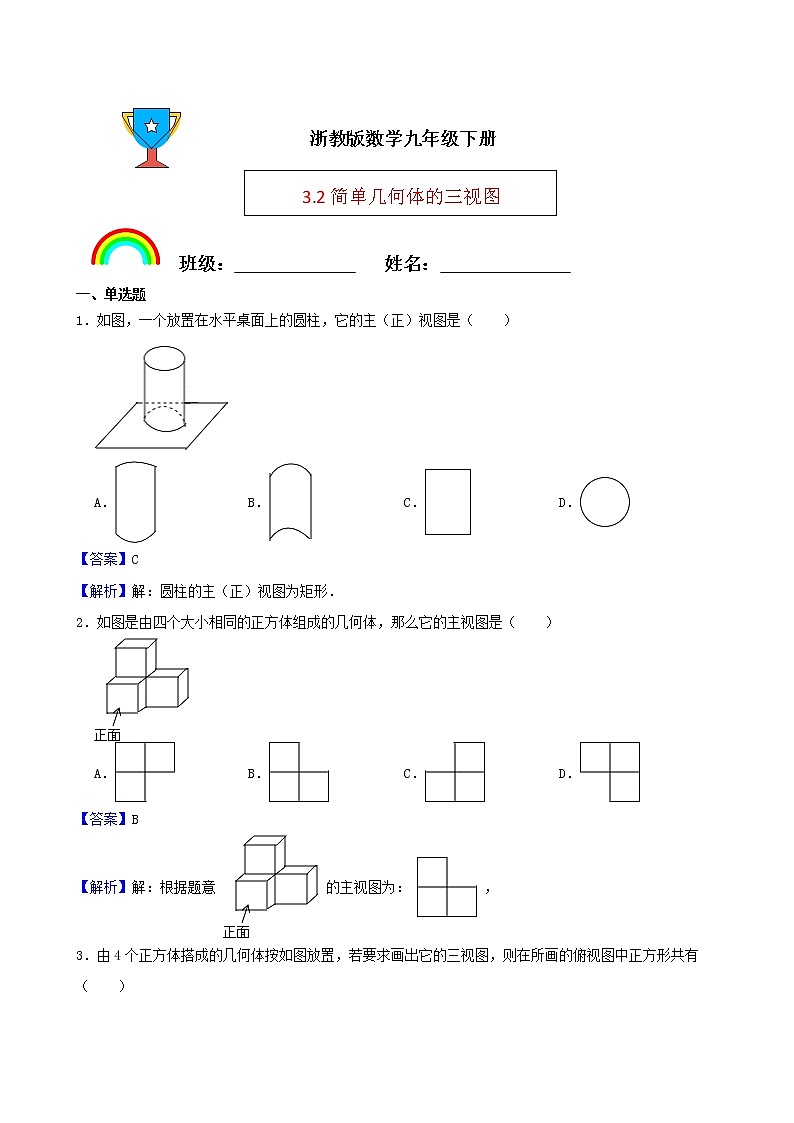
2.如图是由四个大小相同的正方体组成的几何体,那么它的主视图是( )
A.B.C.D.
【答案】B
【解析】解:根据题意 的主视图为: ,
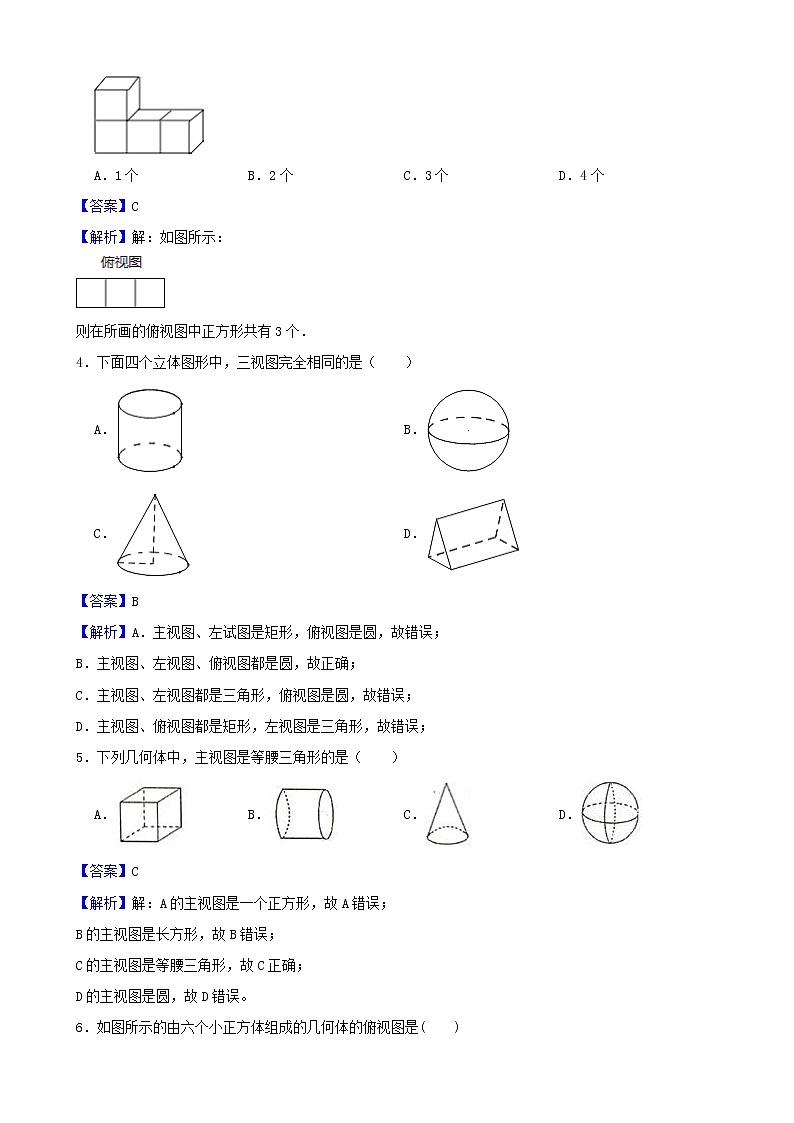
3.由4个正方体搭成的几何体按如图放置,若要求画出它的三视图,则在所画的俯视图中正方形共有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】解:如图所示:
则在所画的俯视图中正方形共有3个.
4.下面四个立体图形中,三视图完全相同的是( )
A.B.
C.D.
【答案】B
【解析】A.主视图、左试图是矩形,俯视图是圆,故错误;
B.主视图、左视图、俯视图都是圆,故正确;
C.主视图、左视图都是三角形,俯视图是圆,故错误;
D.主视图、俯视图都是矩形,左视图是三角形,故错误;
5.下列几何体中,主视图是等腰三角形的是( )
A.B.C.D.
【答案】C
【解析】解:A的主视图是一个正方形,故A错误;
B的主视图是长方形,故B错误;
C的主视图是等腰三角形,故C正确;
D的主视图是圆,故D错误。
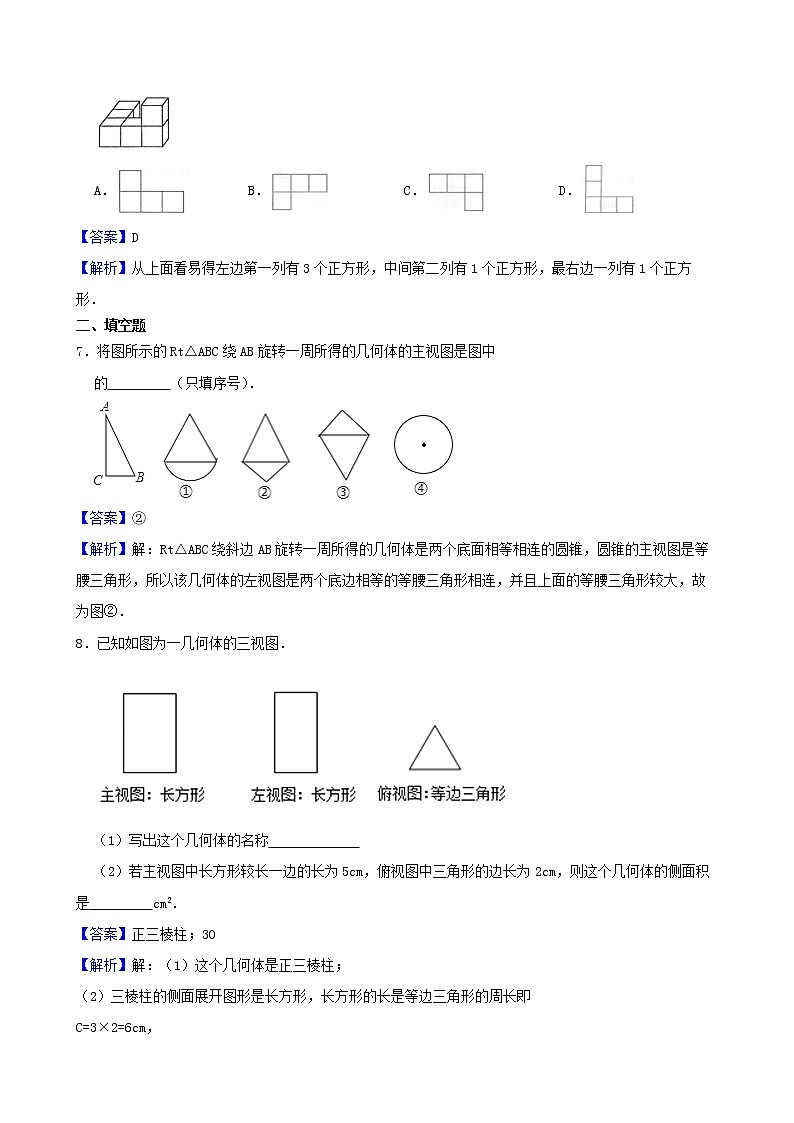
6.如图所示的由六个小正方体组成的几何体的俯视图是( )
A.B.C.D.
【答案】D
【解析】从上面看易得左边第一列有3个正方形,中间第二列有1个正方形,最右边一列有1个正方形.
二、填空题
7.将图所示的Rt△ABC绕AB旋转一周所得的几何体的主视图是图中
的 (只填序号).
【答案】②
【解析】解:Rt△ABC绕斜边AB旋转一周所得的几何体是两个底面相等相连的圆锥,圆锥的主视图是等腰三角形,所以该几何体的左视图是两个底边相等的等腰三角形相连,并且上面的等腰三角形较大,故为图②.
8.已知如图为一几何体的三视图.
(1)写出这个几何体的名称
(2)若主视图中长方形较长一边的长为5cm,俯视图中三角形的边长为2cm,则这个几何体的侧面积是 cm2.
【答案】正三棱柱;30
【解析】解:(1)这个几何体是正三棱柱;
(2)三棱柱的侧面展开图形是长方形,长方形的长是等边三角形的周长即
C=3×2=6cm,
根据题意可知主视图的长方形的长是三棱柱的高,所以三棱柱侧面展开图形的面积为:
S=6×5=30cm2.
答:这个几何体的侧面面积为30cm2.
9.如图,一长方体木板上有两个洞,一个是正方形形状的,一个是圆形形状的,对于以下4种几何体,你觉得哪一种作为塞子既可以堵住圆形空洞又可以堵住方形空洞? (填序号).
【答案】②
【解析】解:圆柱的俯视图是圆,可以堵住圆形空洞,它的正视图和左视图是长方形,可以堵住方形空洞,故圆柱是最佳选项,
10.如图是某圆锥的主视图和左视图,该圆锥的侧面积是 .
【答案】20π
【解析】解:由题可得,圆锥的底面直径为8,高为3,
则圆锥的底面周长为8π,
圆锥的母线长为 32+(8÷2)2=5 ,
则圆锥的侧面积 =12×8π×5=20π .
11.已知圆锥如图所示放置,.其主视图面积为12,俯视图的周长为6π,则该圆锥的侧面积为 .
【答案】15 π
【解析】∵俯视图的周长为6π, ∴底面直径为6π÷π=6,
又∵主视图面积12, ∴主视图的高为:12×2÷6=4,
∴圆锥母线的长为: (6÷2)2+42=5 , ∴该圆锥的侧面积为:S=πrl=15π( cm2 ).
12.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 .
【答案】48+123
【解析】三视图就是主视图(正视图)、俯视图、左视图的总称。从物体的前面向后面投射所得的视图称主视图(正视图)——能反映物体的前面形状;从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状;从物体的左面向右面投射所得的视图称左视图——能反映物体的左面形状。利用知识:主府长对正,主左高平齐,府左宽相等,得该几何体底面正六边形,AB=4,正六边形被分成6个全等的等边三角形,边长AC=2
S底=6S△AOD=6×12×2×3=63
S侧=2×4=8
该几何体的表面积为2 S底 +6 S侧 =48+12 3
三、解答题
13.学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);
(2)分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.
【答案】解:由题意得:
(1)2+1.5(x﹣1)=1.5x+0.5
(2)由三视图可知共有12个碟子
∴叠成一摞的高度=1.5×12+0.5=18.5(cm)
【解析】由表中给出的碟子个数与碟子高度的规律,可以看出碟子数为x时,碟子的高度为2+1.5(x﹣1).
14.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积.(结果可保留根号)
【答案】解 根据该几何体的三视图知道其是一个六棱柱,
∵其高为12cm,底面半径为5,
∴其侧面积为6×5×12=360cm2
密封纸盒的底面积为:12×5×32×5×12=753cm2,
∴其全面积为:(75 3+360)cm2.
【解析】根据该几何体的三视图知道其是一个六棱柱,其表面积是六个面的面积加上两个底的面积.
15.如图物体是由6个相同的小正方体搭成的,请你画出它的三视图.
【答案】解:如图所示:
【解析】主视图有3列,每列小正方形数目分别为2,2,1;左视图有2列,每列小正方形数目分别为2,1;俯视图有3列,每行小正方形数目分别为1,2,1.
16.分别画出如图所示几何体的三视图,并求几何体的表面积和体积.
【答案】解:①
由勾股定理易得主视图中等腰三角形的腰长为5cm,
表面积为:6×2×2+8×2×2+2×6×4÷2+2×5×8+6×8=208cm2;
体积为:(6×2+6×4÷2)×8=192cm3;
②
表面积为:9×4.5×2+4.5×9×2+(4.5×4.5﹣1.5×3)×2+3×9×2=247.5cm2;
体积为:(4.5×4.5﹣1.5×3)×9=141.75cm3;
③
表面积为:15×5×2+10×15+(2×10×5﹣π×32)+ 12 π(10﹣2﹣2)×15=(460+36π)cm2;
体积为:(10×5﹣ 12 π×32)×15=(750﹣67.5π)cm3.
【解析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;计算表面积找到所有面的和相加即可;所给几何体的体积均为相应的底面积乘高,把相关数值代入即可求解.
17.如图,分别从正面、左面、上面观察该立体图形,能得到什么平面图形.
【答案】解:从正面看该几何体是三角形,从左面看该几何体是长方形,从上面看该几何体是一长方形中带一条竖线.
【解析】细心观察图中几何体的摆放,从正面看该几何体是三角形,从左面看该几何体是长方形,从上面看该几何体是一长方形中带一条竖线.
18.由几个相同的边长为1的小立方块搭成的几何体的俯视图如图,方格中的数字表示该位置的小立方块的个数.
(1)请在图方格纸中分别画出该几何体的主视图和左视图;
(2)根据三视图,这个几何体的表面积为多少个平方单位?(包括面积)
【答案】解:(1)如图所示:
;
(2)能看到的:第一层表面积为12,第二层表面积为:7,第三层表面积为:5,
∴这个几何体的表面积为24个平方单位.
答案:这个几何体的表面积为24个平方单位.
【解析】依据简单几何体知识即可得出答案。碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
浙教版九年级下册第三章 投影与三视图3.2 简单几何体的三视图优秀达标测试: 这是一份浙教版九年级下册第三章 投影与三视图3.2 简单几何体的三视图优秀达标测试,共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版九年级下册3.2 简单几何体的三视图随堂练习题: 这是一份浙教版九年级下册3.2 简单几何体的三视图随堂练习题,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学浙教版九年级下册3.2 简单几何体的三视图优秀课后测评: 这是一份初中数学浙教版九年级下册3.2 简单几何体的三视图优秀课后测评,文件包含第3章三视图与表面展开图32简单几何体的三视图pdf、第3章三视图与表面展开图32简单几何体的三视图教材参考答案pdf、第3章三视图与表面展开图32简单几何体的三视图本书习题参考答案pdf等3份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。














