苏州中学园区校初三数学2022-2023学年10月月考试卷（含答案）

这是一份苏州中学园区校初三数学2022-2023学年10月月考试卷（含答案），共21页。试卷主要包含了三角形的内心是，如图，⊙O是△ABC的内切圆等内容，欢迎下载使用。

2022年10月初三数学阶段性测试
一．单选题（每题3分，共24分）
1．三角形的内心是（　　）
A．三角形三条中线的交点 B．三角形三条高线的交点
C．三角形三边垂直平分线的交点 D．三角形三条角平分线的交点
2．如图，已知点A，B，C依次在⊙O上，∠B﹣∠A＝40°，则∠AOB的度数为（　　）
A．70° B．72° C．80° D．84°

第2题 第3题 第5题
3．如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠C＝50°，则∠B的大小等于（　　）
A．20° B．25° C．40° D．50°
4．若圆锥的底面圆半径是，圆锥的侧面展开图是一个半径为扇形，则此扇形的圆心角为（　　）
A．60° B．90° C．120° D．150°
5．如图，⊙O是△ABC的内切圆．若∠BAC＝70°，则∠BOC的度数为（　　）
A．110° B．125° C．135° D．140°
6．一圆锥体形状的水晶饰品，母线长是10cm，底面圆的直径是5cm，点A为圆锥底面圆周上一点，从A点开始绕圆锥侧面缠一圈彩带回到A点，则彩带最少用多少厘米（接口处重合部分忽略不计）（　　）
A．10πcm B．10cm C．5πcm D．5cm
7．如图，将⊙O沿弦AB折叠，恰好经过圆心O，若⊙O的半径为3，则劣的长为（　　）
A．π B．π C．2π D．3π

第7题 第8题
8．如图，在等边△ABC中，AB＝4，点D为AB的中点，动点E、F分别在AD、BC上，且EF＝2，作△BEF的外接圆⊙O，交AC于点G、H．当动点E从点D向点A运动时，线段GH长度的变化情况为（　　）
A．一直不变 B．一直变大 C．先变小再变大 D．先变大再变小
二、填空题（每题3分，共24分）
9．直角三角形的两条直角边分别是5和12，则它的内切圆半径为　 　．
10．如图，已知PA，PB分别切⊙O于A、B，CD切⊙O于E，PO＝13，AO＝5，则△PCD周长为　 　．

第10题 第11题 第12题
11．如图，在矩形ABCD中，AB＝6，BC＝4，⊙O是以AB为直径的圆，则直线DC与⊙O的位置关系是　 　．
12．如图所示，一个宽为2cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），那么该光盘的直径是 　 　cm．
13．一条弦把圆分成1：4两部分，那么这条弦所对的圆周角的度数为 　 　．
14．如图，正六边形ABCDEF的边长为2，以A为圆心，AC的长为半径画弧，得，连接AC，AE，则图中阴影部分的面积为 　 　．
15．如图，在⊙O中，AD⊥BC，连接AB、CD，当AB＝2，CD＝6时，则⊙O半径长为 　 　．

第14题 第15题 第16题
16．在矩形ABCD中，AB＝10，AD＝6，点N是线段BC的中点，点E，G分别为射线DA，线段AB上的动点，CE交以DE为直径的圆于点M，则GM+GN的最小值为　 　．
三、解答题（共52分）
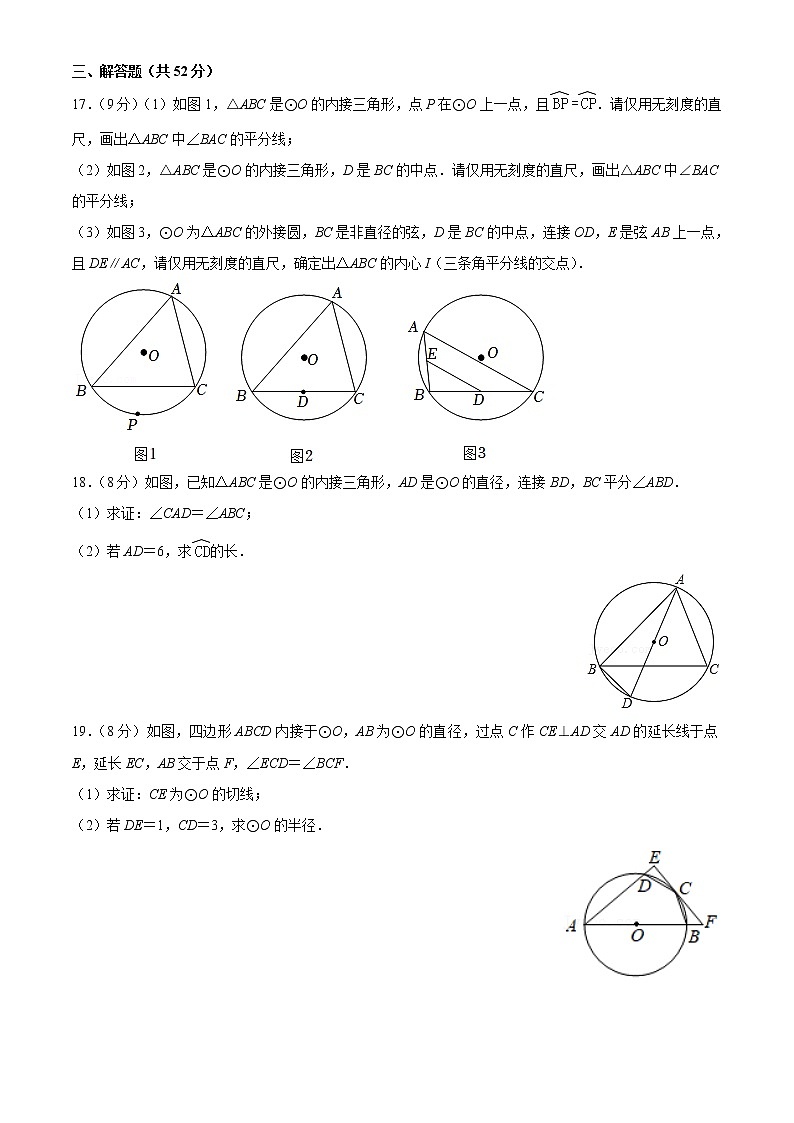
17．（9分）（1）如图1，△ABC是⊙O的内接三角形，点P在⊙O上一点，且．请仅用无刻度的直尺，画出△ABC中∠BAC的平分线；
（2）如图2，△ABC是⊙O的内接三角形，D是BC的中点．请仅用无刻度的直尺，画出△ABC中∠BAC的平分线；
（3）如图3，⊙O为△ABC的外接圆，BC是非直径的弦，D是BC的中点，连接OD，E是弦AB上一点，且DE∥AC，请仅用无刻度的直尺，确定出△ABC的内心I（三条角平分线的交点）．

18．（8分）如图，已知△ABC是⊙O的内接三角形，AD是⊙O的直径，连接BD，BC平分∠ABD．
（1）求证：∠CAD＝∠ABC；
（2）若AD＝6，求的长．

19．（8分）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，过点C作CE⊥AD交AD的延长线于点E，延长EC，AB交于点F，∠ECD＝∠BCF．
（1）求证：CE为⊙O的切线；
（2）若DE＝1，CD＝3，求⊙O的半径．


20．（9分）【了解概念】
我们知道，折线段是由两条不在同一直线上且有公共端点的线段组成的图形．如图1，线段MQ、QN组成折线段MQ．N若点P在折线段MQN上，MP＝PQ+QN，则称点P是折线段MQN的中点．

【理解应用】
（1）如图2，⊙O的半径为2，PA是⊙O的切线，A为切点，点B是折线段POA的中点．若∠APO＝30°，则PB＝　 　；
（2）如图3，⊙O中，，D是上一点，AH⊥BD，垂足为H．求证：点H是折线段BDC的中点；
【拓展提升】
（3）如图4，A，P，B，C是⊙O上的四个点，AB＝AC＝2，求PB・PC的值．

21．（8分）阅读以下材料，并按要求完成相应的任务．
已知平面上两点A、B，则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．
阿氏圆基本解法：构造三角形相似．
【问题】如图1，在平面直角坐标系中，在x轴，y轴上分别有点C（m，0），D（0，n），点P是平面内一动点，且OP＝r，设＝k，求PC+kPD的最小值．

阿氏圆的关键解题步骤：
第一步：如图1，在OD上取点M，使得OM：OP＝OP：OD＝k；
第二步：证明kPD＝PM；第三步：连接CM，此时CM即为所求的最小值．
下面是该题的解答过程（部分）：
解：在OD上取点M，使得OM：OP＝OP：OD＝k，
又∵∠POD＝∠MOP，∴△POM∽△DOP．
任务：
（1）将以上解答过程补充完整．
（2）如图2，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为△ABC内一动点，满足CD＝2，利用（1）中的结论，请直接写出AD+BD的最小值．

22．（10分）如图①，小慧同学把一个正三角形纸片（即△OAB）放在直线l1上．OA边与直线l1重合，然后将三角形纸片绕着顶点A按顺时针方向旋转120°，此时点O运动到了点O1处，点B运动到了点B1处；小慧又将三角形纸片AO1B1，绕点B1按顺时针方向旋转120°，此时点A运动到了点A1处，点O1运动到了点O2处（即顶点O经过上述两次旋转到达O2处）．
小慧还发现：三角形纸片在上述两次旋转的过程中．顶点O运动所形成的图形是两段圆弧，即和，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和．
小慧进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l2上，OA边与直线l2重合，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时点O运动到了点O1处（即点B处），点C运动到了点C1处，点B运动到了点B2处，小慧又将正方形纸片AO1C1B1绕顶点B1按顺时针方向旋转90°，…．按上述方法经过若干次旋转后，她提出了如下问题：
问题①：若正方形纸片OABC按上述方法经过3次旋转，求顶点O经过的路程，并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积；若正方形纸片OABC按上述方法经过5次旋转．求顶点O经过的路程；
问题②：正方形纸片OABC按上述方法经过多少次旋转，顶点O经过的路程是？
请你解答上述两个问题。

∴∠B＝∠OAB，
∵∠AOC＝∠B+∠OAB＝40°，
∴∠B＝20°，
故选：A．

4．若圆锥的底面圆半径是，圆锥的侧面展开图是一个半径为扇形，则此扇形的圆心角为（　　）
A．60° B．90° C．120° D．150°
【分析】先由半径求得圆锥底面周长，再由扇形的圆心角的度数＝圆锥底面周长×180÷3π计算．
【解答】解：圆锥底面周长＝2×π×＝2π，
∴扇形的圆心角的度数＝2π×180÷3π＝120°．
故选：C．
5．B
6．一圆锥体形状的水晶饰品，母线长是10cm，底面圆的直径是5cm，点A为圆锥底面圆周上一点，从A点开始绕圆锥侧面缠一圈彩带回到A点，则彩带最少用多少厘米（接口处重合部分忽略不计）（　　）
A．10πcm B．10cm C．5πcm D．5cm
【分析】利用圆锥侧面展开图的弧长等于底面圆的周长，进而得出扇形圆心角的度数，再利用勾股定理求出AA′的长．
【解答】解：由两点间直线距离最短可知，圆锥侧面展开图AA′最短，
由题意可得出：OA＝OA′＝10cm，
＝＝5π，
解得：n＝90°，
∴∠AOA′＝90°，
∴AA′＝＝10（cm），
故选：B．

7．如图，将⊙O沿弦AB折叠，恰好经过圆心O，若⊙O的半径为3，则劣的长为（　　）

A．π B．π C．2π D．3π

11．如图，在矩形ABCD中，AB＝6，BC＝4，⊙O是以AB为直径的圆，则直线DC与⊙O的位置关系是　相离　．

【分析】AB为直径，AB＝6，则半径是3；矩形ABCD中，BC＝4，则圆心到CD的距离为4．根据距离大于半径判定相离．
【解答】解：∵矩形ABCD中，BC＝4，
∴圆心到CD的距离为4．
∵AB为直径，AB＝6，
∴半径是3．
∵4＞3，∴直线DC与⊙O相离．
12．如图所示，一个宽为2cm的刻度尺在圆形光盘上移动，当刻度尺的一边与光盘相切时，另一边与光盘边缘两个交点处的读数恰好是“2”和“10”（单位：cm），那么该光盘的直径是 　10　cm．

【分析】本题先根据垂径定理构造出直角三角形，然后在直角三角形中已知弦长和弓形高，根据勾股定理求出半径，从而得解．
【解答】解：如图，设圆心为O，弦为AB，切点为C．如图所示．则AB＝8cm，CD＝2cm．
连接OC，交AB于D点．连接OA．
∵尺的对边平行，光盘与外边缘相切，
∴OC⊥AB．
∴AD＝4cm．
设半径为Rcm，则R2＝42+（R﹣2）2，
解得R＝5，
∴该光盘的直径是10cm．
故答案为：10

13．一条弦把圆分成1：4两部分，那么这条弦所对的圆周角的度数为 　36°或144°　．
【分析】根据题意画出图形，得出两种情况，求出两段弧的度数，即可求出答案．

【分析】找出M点的运动轨迹，同时通过作点N关于AB的对称点N'的方式可以将GN进行转换．
【解答】解：如图所示，作N关于AB的对称点N'，取DC中点F，连接DM，FM，GN'．

可得GN＝GN'，
∵M在以DE为直径的圆上，
∴DM⊥EC，
∴△DMC为直角三角形，
∵F为Rt△DMC斜边的中点，
∴MF＝＝＝5，
此时当MF，MG，GN'三边共线时，有MF+MG+GN'长度的最小值等于FN'，
∵F，N分别是DC，CB的中点，
∴FC＝＝5，BN'＝BN＝＝3，
∴CN'＝BC+BN'＝9，
∴FN'＝＝，
∴MF+MG+GN'长度的最小值为，
∵MF＝5，GN＝GN′
∴GM+GN的最小值为﹣5，
故答案为：．
17．（1）如图1，△ABC是⊙O的内接三角形，点P在⊙O上一点，且．请仅用无刻度的直尺，画出△ABC中∠BAC的平分线；
（2）如图2，△ABC是⊙O的内接三角形，D是BC的中点．请仅用无刻度的直尺，画出△ABC中∠BAC的平分线；
（3）如图3，⊙O为△ABC的外接圆，BC是非直径的弦，D是BC的中点，连接OD，E是弦AB上一点，且DE∥AC，请仅用无刻度的直尺，确定出△ABC的内心I（三条角平分线的交点）．

【分析】（1）连接AP，则AP平分∠BAC；
（2）延长OD交⊙O于E，依据垂径定理即可得到E为的中点，连接AE，则AE平分∠BAC；
（3）依据平行线分线段成比例定理即可得到E为AB的中点，延长OD，OE，根据垂径定理，即可得到G，F分别为，的中点，进而得出CF平分∠ACB，AG平分∠BAC，则交点I即为△ABC的内心．
【解答】解：（1）连接AP，则AP平分∠BAC．

（2）如图2所示，AE即为∠BAC的平分线．

（3）如图2所示，点I即为所求．

18．如图，已知△ABC是⊙O的内接三角形，AD是⊙O的直径，连接BD，BC平分∠ABD．
（1）求证：∠CAD＝∠ABC；
（2）若AD＝6，求的长．

【分析】（1）由角平分线的性质和圆周角定理可得∠DBC＝∠ABC＝∠CAD；
（2）由圆周角定理可得，由弧长公式可求解．
【解答】解：（1）∵BC平分∠ABD，
∴∠DBC＝∠ABC，
∵∠CAD＝∠DBC，
∴∠CAD＝∠ABC；
（2）∵∠CAD＝∠ABC，
∴＝，
∵AD是⊙O的直径，AD＝6，
∴的长＝××π×6＝π．
19．如图，四边形ABCD内接于⊙O，AB为⊙O的直径，过点C作CE⊥AD交AD的延长线于点E，延长EC，AB交于点F，∠ECD＝∠BCF．
（1）求证：CE为⊙O的切线；
（2）若DE＝1，CD＝3，求⊙O的半径．

【分析】（1）如图1，连接OC，先根据四边形ABCD内接于⊙O，得∠CDE＝∠OBC，再根据等量代换和直角三角形的性质可得∠OCE＝90°，由切线的判定可得结论；
（2）如图2，过点O作OG⊥AE于G，连接OC，OD，则∠OGE＝90°，先根据三个角是直角的四边形是矩形得四边形OGEC是矩形，设⊙O的半径为x，根据勾股定理列方程可得结论．
【解答】（1）证明：如图1，连接OC，

∵OB＝OC，
∴∠OCB＝∠OBC，
∵四边形ABCD内接于⊙O，
∴∠CDE＝∠OBC，
∵CE⊥AD，
∴∠E＝∠CDE+∠ECD＝90°，
∵∠ECD＝∠BCF，
∴∠OCB+∠BCF＝90°，
∴∠OCE＝90°，即OC⊥EF，
∵OC是⊙O的半径，
∴CE为⊙O的切线；
（2）解：如图2，过点O作OG⊥AE于G，连接OC，OD，则∠OGE＝90°，
∵∠E＝∠OCE＝90°，
∴四边形OGEC是矩形，
∴OC＝EG，OG＝EC，

设⊙O的半径为x，
Rt△CDE中，CD＝3，DE＝1，
∴EC＝＝2，
∴OG＝2，GD＝x﹣1，OD＝x，
由勾股定理得：OD2＝OG2+DG2，
∴x2＝（2）2+（x﹣1）2，
解得：x＝4.5，
∴⊙O的半径是4.5．
20．【了解概念】
我们知道，折线段是由两条不在同一直线上且有公共端点的线段组成的图形．如图1，线段MQ、QN组成折线段MQ．N若点P在折线段MQN上，MP＝PQ+QN，则称点P是折线段MQN的中点．

【理解应用】
（1）如图2，⊙O的半径为2，PA是⊙O的切线，A为切点，点B是折线段POA的中点．若∠APO＝30°，则PB＝　3　；
（2）如图3，⊙O中，，D是上一点，AH⊥BD，垂足为H．求证：点H是折线段BDC的中点；
【拓展提升】
（3）如图4，A，P，B，C是⊙O上的四个点，AB＝AC＝2，求PB・PC的值．
【分析】（1）由切线的性质得出OA⊥PA，由∠APO＝30°，OA＝2，得出OP＝4，再根据“折线段中点的定义”即可得到答案；
（2）先证明△ABM为等腰三角形，再证明△AMC为等腰三角形，继而得出DC＝DM，进一步即可证明结论；
（3）作AE⊥PC于点E，根据（2）的结论和勾股定理表示出PB和PC的长度，进一步计算即可得出PB・PC的值．
【解答】解：（1）∵PA是⊙O的切线，
∴OA⊥PA，
∵∠APO＝30°，OA＝2，
∴OP＝4，
∴OP+OA＝4+2＝6，
∵点B是折线段POA的中点，
∴PB＝（PA+OA）＝×6＝3，
故答案为：3；
（2）如图，延长BD到M使BH＝HM，连接AM、CM，

∵AH⊥BD，BH＝HM，
∴AM＝AB，
∴∠ABM＝∠AMB，
∵∠ACD＝∠ABD，
∴∠ACD＝∠AMD，
∵AM＝AC＝AB，
∴△AMC是等腰三角形，
∴∠ACM＝AMC，
∴∠ACM﹣∠ACD＝∠AMC﹣∠AMB，
∴∠DCM＝∠DMC，
∴DC＝DM，
∵HM＝DM+DH，
∴HM＝DC+DH，
∵HM＝BH，
∴BH＝HD+DC，
∴点H是折线段BDC的中点；
（3）如图，作AE⊥PC于点E，

由（2）可知E为折线段CPB中点，即CE＝EP+PB，
∴PB＝CE﹣EP，
在Rt△AEC中，CE＝＝，
在Rt△AEP中，EP＝＝，
∴PB＝﹣，
∵PC＝CE+EP
＝+，
∴PB•PC＝（﹣）（+）
＝（12﹣AE2）﹣（5﹣AE2）
＝12﹣AE2﹣5+AE2
＝7．
21．阅读以下材料，并按要求完成相应的任务．
已知平面上两点A、B，则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．
阿氏圆基本解法：构造三角形相似．
【问题】如图1，在平面直角坐标系中，在x轴，y轴上分别有点C（m，0），D（0，n），点P是平面内一动点，且OP＝r，设＝k，求PC+kPD的最小值．

阿氏圆的关键解题步骤：
第一步：如图1，在OD上取点M，使得OM：OP＝OP：OD＝k；
第二步：证明kPD＝PM；第三步：连接CM，此时CM即为所求的最小值．
下面是该题的解答过程（部分）：
解：在OD上取点M，使得OM：OP＝OP：OD＝k，
又∵∠POD＝∠MOP，∴△POM∽△DOP．
任务：
（1）将以上解答过程补充完整．
（2）如图2，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为△ABC内一动点，满足CD＝2，利用（1）中的结论，请直接写出AD+BD的最小值．
【分析】（1）在OD上取点M，使得OM：OP＝OP：OD＝k，利用相似三角形的性质以及两点之间线段最短解决问题即可．
（2）利用（1）中结论计算即可．
【解答】解（1）在OD上取点M，使得OM：OP＝OP：OD＝k，
又∵∠POD＝∠MOP，
∴△POM∽△DOP．
∴MP：PD＝k，
∴MP＝kPD，
∴PC+kPD＝PC+MP，当PC+kPD取最小值时，PC+MP有最小值，即C，P，M三点共线时有最小值，
利用勾股定理得．
（2）∵AC＝m＝4，＝，在CB上取一点M，使得CM＝CD＝，

∴的最小值为．
22．如图①，小慧同学把一个正三角形纸片（即△OAB）放在直线l1上．OA边与直线l1重合，然后将三角形纸片绕着顶点A按顺时针方向旋转120°，此时点O运动到了点O1处，点B运动到了点B1处；小慧又将三角形纸片AO1B1，绕点B1按顺时针方向旋转120°，此时点A运动到了点A1处，点O1运动到了点O2处（即顶点O经过上述两次旋转到达O2处）．
小慧还发现：三角形纸片在上述两次旋转的过程中．顶点O运动所形成的图形是两段圆弧，即和，顶点O所经过的路程是这两段圆弧的长度之和，并且这两段圆弧与直线l1围成的图形面积等于扇形A001的面积、△AO1B1的面积和扇形B1O1O2的面积之和．
小慧进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l2上，OA边与直线l2重合，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时点O运动到了点O1处（即点B处），点C运动到了点C1处，点B运动到了点B2处，小慧又将正方形纸片AO1C1B1绕顶点B1按顺时针方向旋转90°，…．按上述方法经过若干次旋转后，她提出了如下问题：