初中18.2.3 正方形当堂检测题

这是一份初中18.2.3 正方形当堂检测题，共9页。


2. 我们知道四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A、B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D处，则点C的对应点C′的坐标为（ ）

A.3,1B.2,1C.1,3D.2,3

3. 如图，Rt△ABC中，∠ACB=90∘，若AB=15cm，则正方形ADEC和正方形BCFG的面积之和为( )

A.150cm2B.200cm2C.225cm2D.无法计算

4. 如图所示，四边形OABC是正方形，边长为3，点A、C分别在x轴、y轴的正半轴上，点D在OA上，且D点的坐标为1,0，P是OB上一动点，则PA+PD的最小值为( )

A.210B.10C.2D.3

5. 如图，P为正方形ABCD内一动点，PA=AB=4，M为PB的中点，则CM的最小值为( )

A.125B.135C.22D.25−2

6. 如图，正方形ABCD的对角线BD是菱形BEFD的一边，菱形BEFD的对角线交正方形ABCD的一边CD于点P，∠FPC的度数是( )

A.135∘B.120∘C.112.5∘D.67.5∘

7. 如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5∘，EF⊥AB，垂足为F，则EF的长为( )

A.4−22B.32−4C.1D.2

8. 已知正方形ABCD，以CD为边作等边△CDE，则∠AED的度数是________．

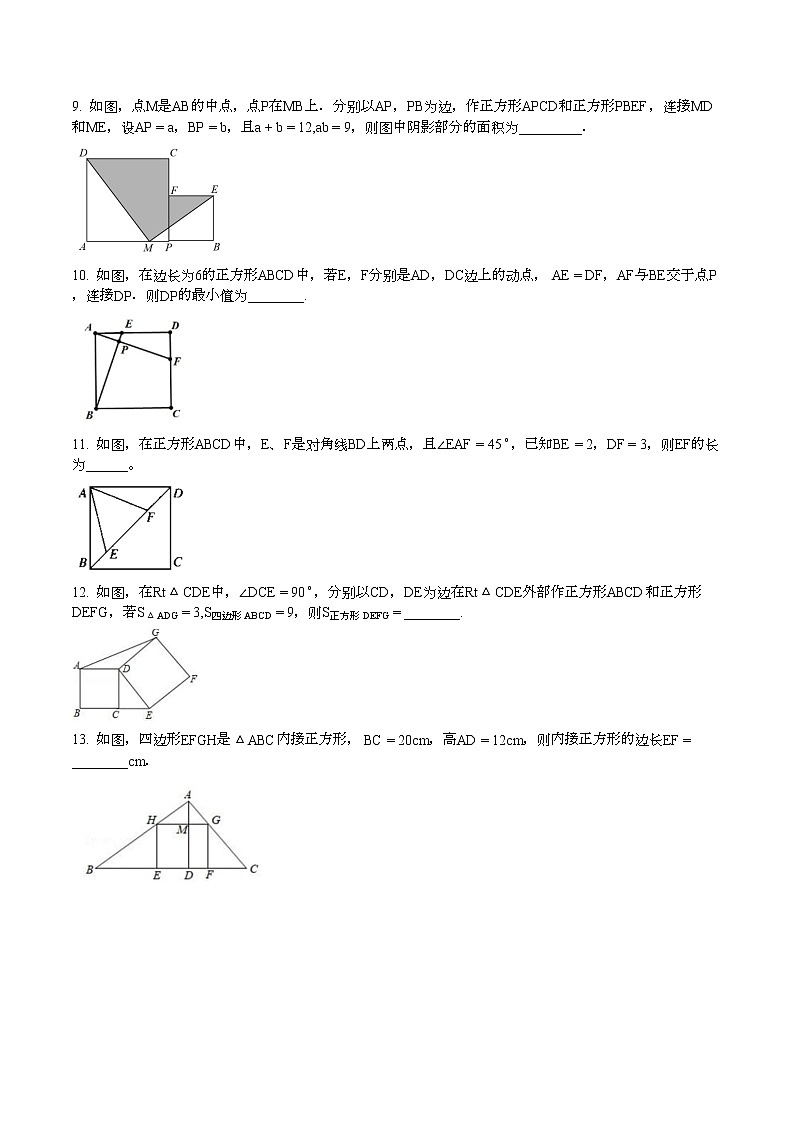
9. 如图，点M是AB的中点，点P在MB上．分别以AP，PB为边，作正方形APCD和正方形PBEF，连接MD和ME，设AP=a，BP=b，且a+b=12,ab=9，则图中阴影部分的面积为_________．

10. 如图，在边长为6的正方形ABCD中，若E，F分别是AD，DC边上的动点， AE=DF，AF与BE交于点P，连接DP．则DP的最小值为________.

11. 如图，在正方形ABCD中，E、F是对角线BD上两点，且∠EAF=45∘，已知BE=2，DF=3，则EF的长为______。

12. 如图，在Rt△CDE中，∠DCE=90∘，分别以CD，DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG，若S△ADG=3,S四边形ABCD=9，则S正方形DEFG=________.

13. 如图，四边形EFGH是△ABC内接正方形， BC=20cm，高AD=12cm，则内接正方形的边长EF=________cm．


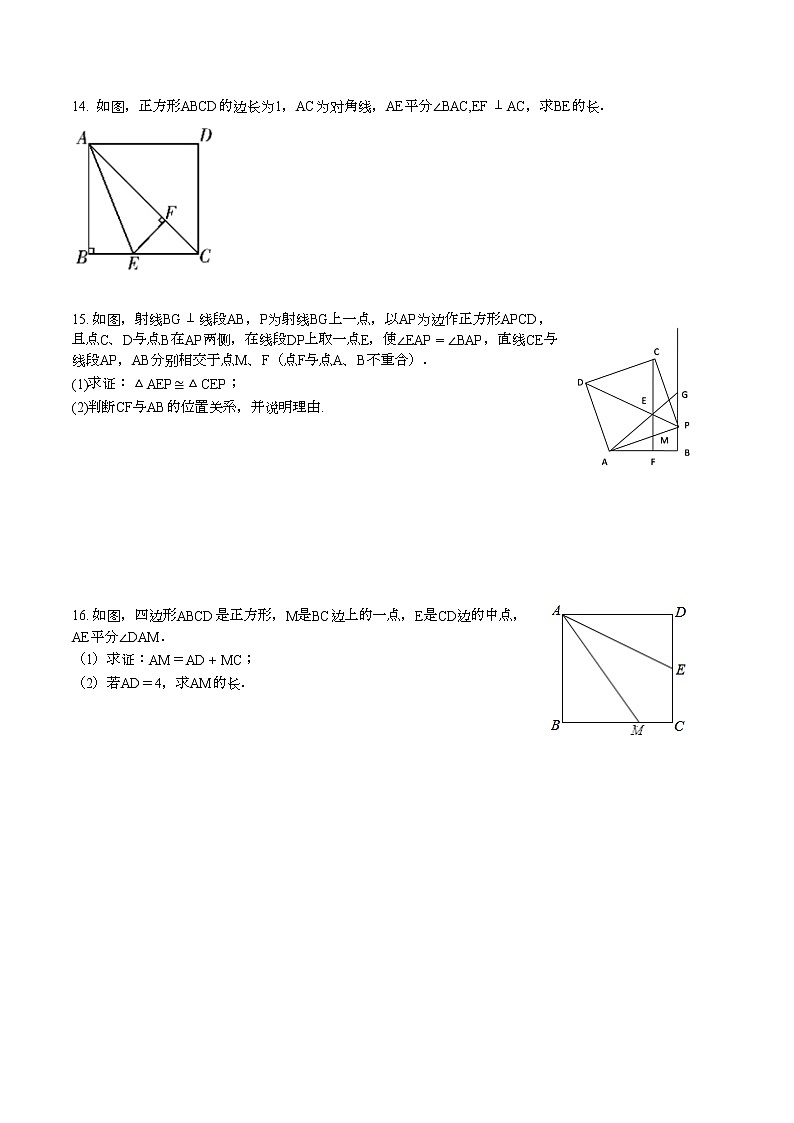
14. 如图，正方形ABCD的边长为1，AC为对角线，AE平分∠BAC,EF⊥AC，求BE的长．


15. 如图，射线BG⊥线段AB，P为射线BG上一点，以AP为边作正方形APCD，且点C、D与点B在AP两侧，在线段DP上取一点E，使∠EAP=∠BAP，直线CE与线段AP，AB分别相交于点M、F（点F与点A、B不重合）．
(1)求证：△AEP≅△CEP；
(2)判断CF与AB的位置关系，并说明理由.

16. 如图，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
（1）求证：AM＝AD+MC；
（2）若AD＝4，求AM的长．

17. 如图，四边形ABCD与四边形AEFG均为正方形，DE与BG交于点H，BG与AE交于点M．
(1)求证：BG=DE；
(2)求证：DH2+GH2=DG2；
(3)将正方形ABCD绕点A逆时针旋转0∘<∠BAE<180∘，设△ABE的面积为S1，△ADG的面积为S2，判断S1与S2大小关系，并证明你的结论．

18. 如图所示，在四边形ABCD中，AD//BC，∠B=90∘，AD=24cm，BC=26cm．动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C出发沿着CB方向向点B以3cm/s的速度运动．点P，Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．

(1)经过多长时间，四边形PQCD是平行四边形？
(2)经过多长时间，四边形PQBA是矩形？
(3)若AB=8，如果Q点的移动速度不变，要使PQBA是正方形，则P点移动速度是多少？
参考答案与试题解析
一、 选择题
1.
【答案】
C
2.
【答案】
D
3.
【答案】
C
4.
【答案】
B
5.
【答案】
D
6.
【答案】
C
7.
【答案】
A
二、 填空题
8.
【答案】
15∘或75∘
9.
【答案】
90
10.
【答案】
35−3
11.
【答案】
3
12.
【答案】
13
13.
【答案】
7.5
三、 解答题
14.
【答案】
解：在正方形ABCD中，∠B=90∘,AB=BC=1
∴ AC=AB2+BC2=2
又AE平分∠BAC,EF⊥AC
∴ ∠BAE=∠FAE，∠B=∠AFE，BE=EF，
∴ △ABE≅△AFEAAS）．
∴ AB=AF，
又∠ECF=45∘，
∴ BE=EF=FC=AC−AF=2−1
15.
【答案】
(1)证明：∵ 四边形APCD为正方形，
∴ DP平分∠APC，PC=PA，
∴ ∠APD=∠CPD=45∘，
又PE=PE，
∴ △AEP≅△CEP；
(2)解：CF⊥AB，理由如下：
∵ △AEP≅△CEP，
∴ ∠EAP=∠FCP．
∵ ∠EAP=∠BAP，
∴ ∠FCP=∠BAP．
∵ ∠FCP+∠CMP=90∘，∠AMF=∠CMP，
∴ ∠AMF+∠PAB=90∘，
∴ ∠AFM=90∘，
∴ CF⊥AB．
16.
【答案】
（1）证明：延长AE、BC交于点N，如图所示.
∵ 四边形ABCD是正方形，
∴ AD//BC，
∴ ∠DAE=∠ENC.
∵ AE平分∠DAM，
∴ ∠DAE=∠MAE，
∴ ∠ENC=∠MAE，
∴ AM=MN.
在△ADE和△NCE中，
∠DAE=∠CNE∠AED=∠CENDE=CE，
∴ △ADE≅△NCEAAS，
∴ AD=NC，
∴ AM=MN=MC+NC=AD+MC.
（2）解：∵ 四边形ABCD是正方形，
∴ AB=BC=AD=4,∠B=90∘.
设MC=x，则BM=4−x,
∴ AM=AB2+BM2=42+4−x2，
∵ AM=AD+MC=4+x，
∴ 42+4−x2=4+x，
解得：x=1，
∴ AM=5.
17.
【答案】
(1)证明：∵ 四边形ABCD与四边形AEFG均为正方形，
∴ ∠BAD=∠EAG=90∘，AG=AE，AB=AD，
∴ ∠BAD+∠BAE=∠EAG+∠BAE，即∠EAD=∠GAB，
∴ △EAD≅△GAB，
∴ BG=DE．
(2)证明：由(1)知△EAD≅△GAB，
∴ ∠BGA=∠DEA．
∵ ∠BGA+∠GMA=90∘，∠AMG=∠EMH，
∴ ∠DEA+∠EMH=90∘,
∴ BG⊥DE,
∴ DH2+GH2=DG2．
(3)解：S1=S2. 证明如下：
过点D作DP⊥GA交GA的延长线于P，过点B作BN⊥AE交AE的延长线于N．
∵ ∠BAE+∠BAP=∠DAP+∠BAP=90∘，
∴ ∠BAE=∠DAP，
∴ △PAD≅△NAB，
∴ DP=BN．
∵ S1=12AE⋅BN，S2=12AG⋅DP，
∴ S1=S2．
18.
【答案】
解：(1)∵ PD//CQ，
∴ 只要当PD=CQ时，四边形PQCD是平行四边形，
设运动时间为t，PD=24−t，CQ=3t，
列式：24−t=3t，
解得t=6，
∴ 经过6秒，四边形PQCD是平行四边形.
(2)∵ AP//BQ且∠B=90∘，
∴ 只要当AP=BQ时，四边形PQAB是矩形，
设运动时间为t，AP=t，BQ=26−3t，
列式：t=26−3t，
解得t=132，
∴ 经过132秒，四边形PQBA是矩形.
(3)当BQ=AB=8时，四边形PQBA是正方形，
设运动时间为t，
列式：26−3t=8，
解得t=6，
∵ PA=6⋅vP=8，
解得vP=43cm/s．