初中数学苏科版七年级下册12.2 证明授课课件ppt

这是一份初中数学苏科版七年级下册12.2 证明授课课件ppt，文件包含122证明pptx、122证明doc等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。

第12章 证明2 证明
现阶段我们在数学上学习的命题由几类？
（包括定义、基本事实和定理）
判定一个命题是真命题的方法:
(1)通过推理的方式,即根据已知的事实来推断未知事实；
(2)人们经过长期实践后而公认为正确的.
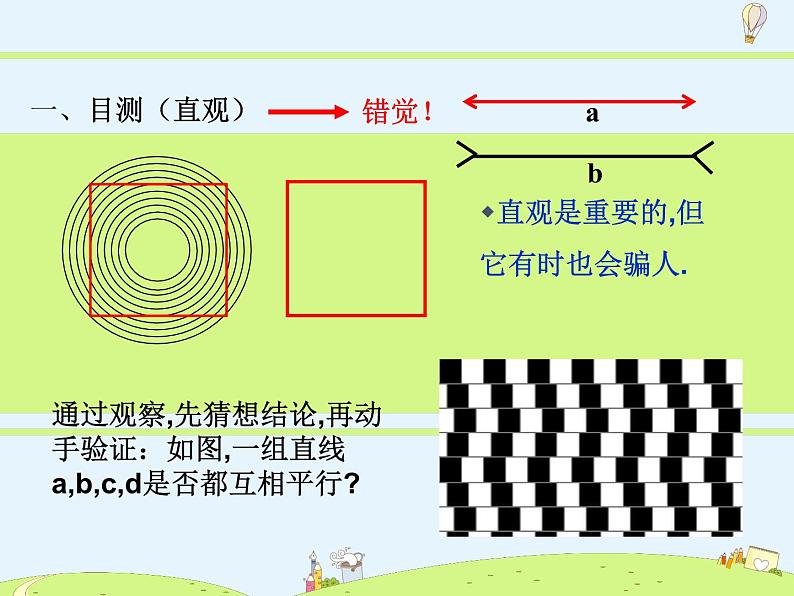
通过观察,先猜想结论,再动手验证：如图,一组直线a,b,c,d是否都互相平行?
直观是重要的,但它有时也会骗人.
如何判断一个命题是真命题？
当n=6时， n2-3n+7 =25不是素数
当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是素数．那么,命题“对于自然数n,代数式n2-3n+7的值都是素数”是真命题吗?
四、判定一个命题是真命题的方法：
通过推理的方式,即根据已知的事实来推断未知事实；
要判定一个命题是真命题，往往需要从命题的条件出发，根据已知的定义、基本事实、定理，一步一步推出结论成立，这样的推理过程叫做证明 。
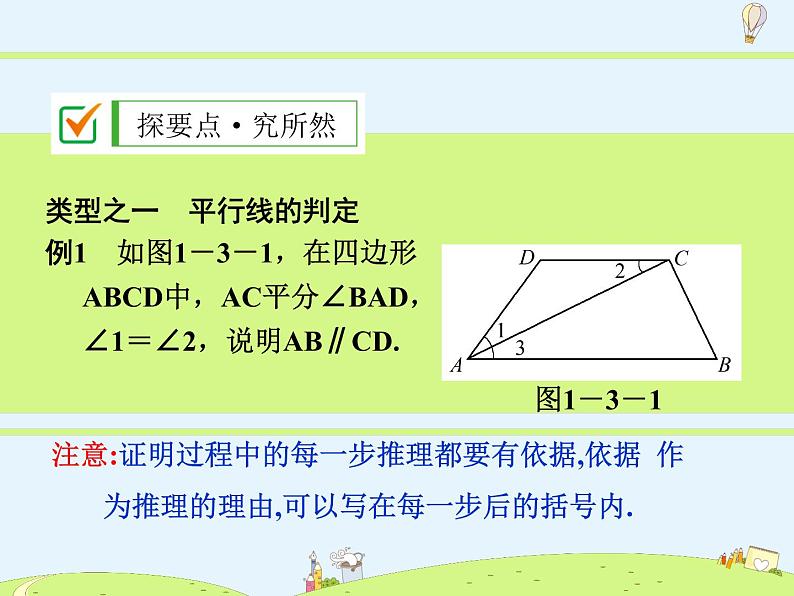
类型之一　平行线的判定例1　如图1－3－1，在四边形ABCD中，AC平分∠BAD，∠1＝∠2，说明AB∥CD.
注意:证明过程中的每一步推理都要有依据,依据 作为推理的理由,可以写在每一步后的括号内.
第2课时 三角形的内角和定理及推论
对于三角形，我们已经有哪些认识？
1.三角形的内角和性质：三角形三个内角的和等于_________．2．三角形的外角定义：由三角形一条边的延长线和另一条相邻的边组成的角．性质1：三角形的一个外角等于与它不相邻的两个___________．性质2：三角形的一个外角大于与它不相邻的任何一个内角．
三角形的三个内角的和等于180°.
如图，∠A，∠B，∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
实验1：先将三角形纸片的一角折向其对边，使顶点落在对边上，折线与对边平行（图1），然后把另处两角相向对折，使其顶点与已折角的顶点相嵌合（图2）、（图3），最后得到（图4）所示的结果。
例1、求证：三角形三个内角的和等于180º.
实验2： 将三角形纸片的顶角剪下，随意将它们拼凑在一起。
在证明三角形的内角和时，小明的想法是把三个角“凑”到A处，他过点A作直线DE//BC，（如图）。他的想法可行吗？
证明　过点A作DE∥BC.则∠C＝∠CAE，∠B＝∠BAD（两直线平行，内错角相等）∴∠BAC+∠B+∠C＝∠BAC+∠BAD+∠CAE　＝∠DAE＝180°（平角的定义）
你还有其他的证明方法么？
3．证明几何命题的格式格式：(1)按照题意画出图形；(2)分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论；(3)在“证明”中写出推理过程．
三角形的内角和的运用例　如图1－3－12，在△ABC中，∠A＝60°，∠B∶∠C＝1∶5.求∠B的度数．