2020-2021年湖北省麻城市某校初三（下）5月月考数学试卷

这是一份2020-2021年湖北省麻城市某校初三（下）5月月考数学试卷，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 在有理数−4，0，−1，3中，最小的数是( )
A.−1B.0C.−4D.3

2. 新型冠状病毒有包膜，直径在60−220纳米之间，平均直径为110纳米左右，颗粒呈圆形或者椭圆形，对紫外线和热敏感，在75%酒精乙醚、甲醛、含氯消毒液等可使其灭活，将110纳米用科学记数法表示为( )（1纳米=10−9米）
A.11×10−7米B.1.1×10−7米C.11×10−8米D.1.1×10−8米

3. 计算(−2a3)2÷a2的结果是( )
A.−2a3B.−2a4C.4a3D.4a4

4. 如图所示几何体的主视图是( )

A.B.C.D.

5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：
根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择( )
A.甲B.乙C.丙D.丁

6. 如图，一条公路的转弯处是一段圆弧(AB），点O是这段弧所在圆的圆心，AB=40m，点C是AB的中点，且CD=10m，则这段弯路所在圆的半径为( )

A.25mB.24mC.30mD.60m

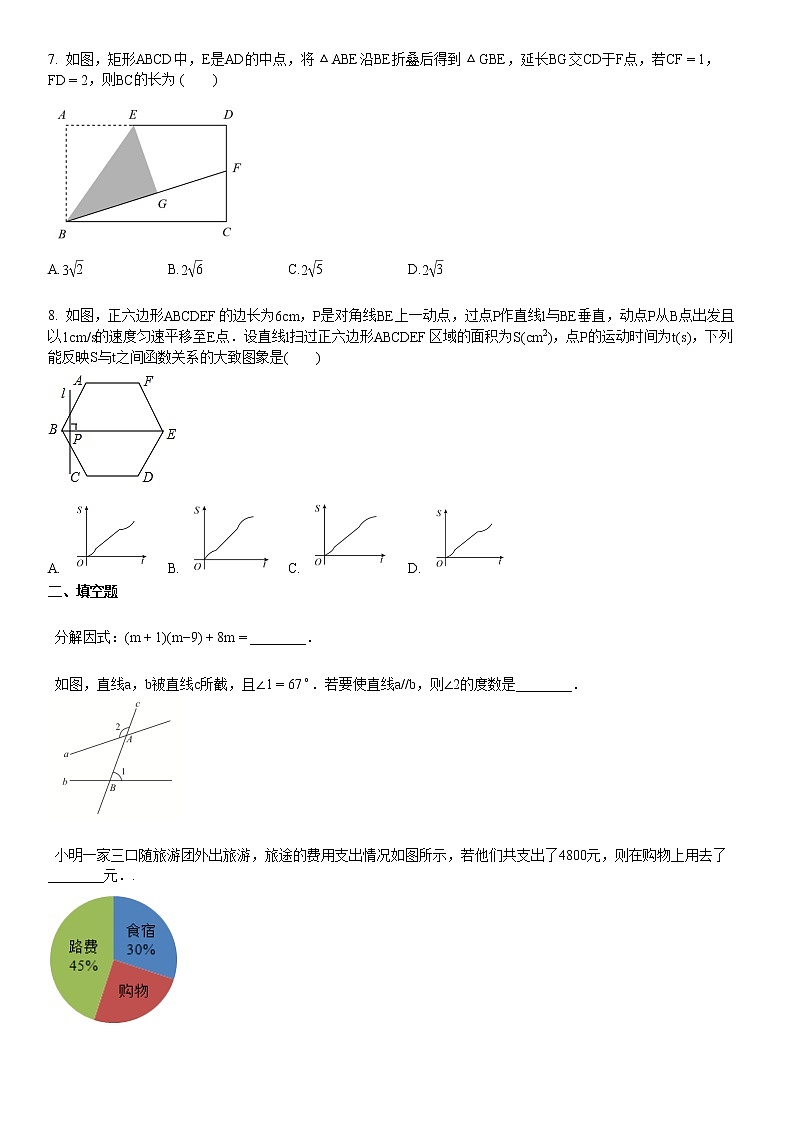
7. 如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交CD于F点，若CF=1，FD=2，则BC的长为 ( )

A.32B.26C.25D.23

8. 如图，正六边形ABCDEF的边长为6cm，P是对角线BE上一动点，过点P作直线l与BE垂直，动点P从B点出发且以1cm/s的速度匀速平移至E点．设直线l扫过正六边形ABCDEF区域的面积为S(cm2)，点P的运动时间为t(s)，下列能反映S与t之间函数关系的大致图象是( )

A.B.C.D.
二、填空题

分解因式：(m+1)(m−9)+8m=________．

如图，直线a，b被直线c所截，且∠1=67∘．若要使直线a//b，则∠2的度数是________．


小明一家三口随旅游团外出旅游，旅途的费用支出情况如图所示，若他们共支出了4800元，则在购物上用去了________元．.


若关于x的不等式x−1≤a有四个非负整数解，a的取值范围是________．

已知x1，x2是一元二次方程x2−4x−7=0的两个实数根，则x12+4x1x2+x22的值是________．

如图，一艘渔船位于灯塔P的北偏东30∘方向，距离灯塔18海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东55∘方向上的B处，此时渔船与灯塔P的距离约为________海里.（结果取整数).(参考数据：sin55∘≈0.8，cs55∘≈0.6，tan55∘≈1.4）


数学的美学无处不在，数学家们研究发现，弹拨琴弦发出声音的音调高低取决于弦的长度，绷得一样紧的几根弦，如果长度的比能够表示成整数的比，发出的声音就比较和谐．例如，三根弦长度之比是15:12:10，把它们绷得一样紧，用同样的力弹拨，它们将分别发出调和的乐声d，mi，s．研究15，12，10这三个数的倒数发现：112−115=110−112．我们称15，12，10这三个数为一组调和数．现有一组调和数：x，6，4(x>6)，则x的值是________．

如图所示，在平面直角坐标系中，已知点A(−1, 0)，B(0,3)，对△OAB连续作旋转变换，依次得到△1，△2，△3，△4，⋯，则△2019的直角顶点的坐标为________．

三、解答题

计算：|3−1|−4sin60∘+16−1 .

如图，△ABC是等边三角形，AE=CD，BQ⊥AD于Q，BE交AD于P.

(1)求证：△ABE≅△CAD；

(2)求∠PBQ的度数.

在不透明的箱子里放有4个乒乓球．每个乒乓球上分别写有数字1，2，3，4，从箱子中摸出一个球记下数字后放回箱中，摇匀后再摸出一个球记下数字．若将第一次摸出的球上的数字记为点的横坐标，第二次摸出的球上的数字记为点的纵坐标．
(1)请用列表法或树状图法写出两次摸球后所有可能的结果；

(2)求这样的点在直线y=5−x上的概率.

如图，在平面直角坐标系xOy中，已知正比例函数y=12x的图象与反比例函数y=kx的图象交于A(a, −2)，B两点．

(1)求反比例函数的表达式和点B的坐标；

(2)P是第一象限内反比例函数图象上一点，过点P作y轴的平行线，交直线AB于点C，连接PO，若△POC的面积为3，求点P的坐标．

我市在创建全国文明城市过程中，决定购买A，B两种树苗对某路段道路进行绿化改造，已知购买A种树苗8棵，B种树苗3棵，需要950元；若购买A种树苗5棵，B种树苗6棵，则需要800元．
(1)求购买A，B两种树苗每棵各需多少元？

(2)考虑到绿化效果和资金周转，购进A种树苗不能少于52棵，且用于购买这两种树苗的资金不能超过7650元，若购进这两种树苗共100棵，则有哪几种购买方案？

(3)某包工队承包种植任务，若种好一棵A种树苗可获工钱30元，种好一棵B种树苗可获工钱20元，在第(2)问的各种购买方案中，种好这100棵树苗，哪一种购买方案所付的种植工钱最少？最少工钱是多少元？

如图，⊙O为等边△ABC的外接圆，D为直径CE延长线上的一点，连接AD，AD=AC．

(1)求证：AD是⊙O的切线；

(2)若CD=6，求阴影部分的面积．

某电子科技公司开发一种新产品，公司对经营的盈亏情况每月最后一天结算1次．在1∼12月份中，公司前x个月累计获得的总利润y（万元）与销售时间x（月）之间满足二次函数关系式y=a(x−ℎ)2+k，二次函数y=a(x−ℎ)2+k的一部分图象如图所示，点A为抛物线的顶点，且点A，B，C的横坐标分别为4，10，12，点A，B的纵坐标分别为−16，20．

(1)试确定函数关系式y=a(x−ℎ)2+k；

(2)分别求出前9个月公司累计获得的利润以及10月份一个月内所获得的利润；

(3)在前12个月中，哪个月该公司一个月内所获得的利润最多？最多利润是多少万元？

已知抛物线y=a(x−2)2+c经过点A(−2, 0)和C(0, 94)，与x轴交于另一点B，顶点为D．
(1)求抛物线的解析式，并写出D点的坐标；

(2)如图，点E，F分别在线段AB，BD上（E点不与A，B重合），且∠DEF=∠A，则△DEF能否为等腰三角形？若能，求出BE的长；若不能，请说明理由；

(3)若点P在抛物线上，且S△PBDS△CBD=m，试确定满足条件的点P的个数．
参考答案与试题解析
2020-2021年湖北省麻城市某校初三（下）5月月考数学试卷
一、选择题
1.
【答案】
C
【考点】
有理数大小比较
【解析】
根据正数大于零，零大于负数进行解答即可
【解答】
解：根据正数大于零，零大于负数，可得−4<−1<0<3，
所以最小的数是−4.
故选C.
2.
【答案】
B
【考点】
科学记数法--表示较小的数
【解析】
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】
解：110纳米=110×10−9米=1.1×10−7米.
故选B.
3.
【答案】
D
【考点】
整式的除法
幂的乘方与积的乘方
【解析】
原式先利用幂的乘方与积的乘方运算法则计算，再利用单项式除以单项式法则计算即可得到结果．
【解答】
解：原式=4a6÷a2=4a4.
故选D．
4.
【答案】
C
【考点】
简单几何体的三视图
【解析】
此题暂无解析
【解答】
解：因为从前面看几何体是一个正方形，
所以该几何体的主视图是正方形.
故选C.
5.
【答案】
A
【考点】
方差
算术平均数
【解析】
无
【解答】
解：∵ x甲=x丙>x乙=x丁，
∴ 从甲和丙中选择一人参加比赛，
∵ s甲2∴ 选择甲参赛.
故选A.
6.
【答案】
A
【考点】
垂径定理的应用
勾股定理
【解析】
根据题意，可以推出AD＝BD＝20，若设半径为r，则OD＝r−10，OB＝r，结合勾股定理可推出半径r的值．
【解答】
解：连结OD，如图所示：
∵ C是弧AB的中点，D为AB的中点，
∴ OC⊥AB，AD=DB=20m.
在Rt△AOD中，OA2=OD2+AD2，
设半径为r得：r2=(r−10)2+202，
解得：r=25m，
∴ 这段弯路所在圆的半径为25m.
故选A.
7.
【答案】
B
【考点】
翻折变换（折叠问题）
矩形的性质
勾股定理
全等三角形的性质与判定
平行线分线段成比例
【解析】
首先过点E作EM⊥BC于M，交BF于N，易证得△ENG≅△BNM(AAS)，MN是△BCF的中位线，根据全等三角形的性质，即可求得GN=MN，由折叠的性质，可得BG=3，继而求得BF的值，又由勾股定理，即可求得BC的长．
【解答】
解：过点E作EM⊥BC于M，交BF于N，
∵ 四边形ABCD是矩形，
∴ ∠A=∠ABC=90∘，AD=BC.
∵ ∠EMB=90∘，
∴ 四边形ABME是矩形，
∴ AE=BM，则CM=DE.
由折叠的性质，得AE=GE，∠EGN=∠A=90∘，
∴ EG=BM.
∵ ∠ENG=∠BNM，
∴ △ENG≅△BNM(AAS)，
∴ NG=NM.
∵ E是AD的中点，
∴ AE=ED=BM=CM.
∵ EM // CD，
∴ BN:NF=BM:CM，
∴ BN=NF，
∴ NM = 12CF = 12，
∴ NG = 12.
∵ BG=AB=CD=CF+DF=3，
∴ BN=BG−NG=3 − 12 = 52，
∴ BF=2BN=5，
∴ BC = BF2 − CF2 = 52 − 12 = 26.
故选B.
8.
【答案】
C
【考点】
动点问题
二次函数的性质
二次函数的图象
二次函数的应用
【解析】
从给出的图象中看，中间位置的图象一致，只要计算两边取值中的图象即可作出判断；
先计算点P从B到G时扫过的面积S，发现是二次函数，且开口向下，可以否定A和B，再计算点P从9≤t≤12时扫过的面积为正六边形的面积−△EMN的面积，计算得到一个开口向下的二次函数，由此作判断．
【解答】
解：如图，连接AC，交BE于G，
在Rt△ABG中，AB=6，∠ABG=60∘，
∴ ∠BAG=30∘，
∴ BG = 12AB=3，
由勾股定理，得AG=62−32=33，
∴ AC=2AG=63，
由题意，得BP=t，
当0≤t≤3时，PM = 3t，
∴ MN=23t，
∴ S=S△BMN =12MN⋅PB=12⋅3t2=32t2，故选项A，B不正确；
当9≤t≤12时，PE=12−t，
∵ ∠MEP=60∘，
∴ tan∠MEP=PMPE，
∴ PM =3(12−t)，
∴ MN=2PM=23(12−t)，
∴ S=S正六边形−S△EMN ，
=2×12(AF+BE)×AG − 12MN⋅PE，
=(6+12)×33−12×23(12−t)(12−t)，
=543 − 3(144−24t+t2)，
=−3t2+243t−903，
又−3<0，则二次函数的开口向下，
故选项C正确，D不正确.
故选C.
二、填空题
【答案】
(m+3)(m−3)
【考点】
因式分解-运用公式法
【解析】
先利用多项式的乘法运算法则展开，合并同类项后再利用平方差公式分解因式即可．
【解答】
解：(m+1)(m−9)+8m，
=m2−9m+m−9+8m，
=m2−9，
=(m+3)(m−3).
故答案为：(m+3)(m−3).
【答案】
113∘
【考点】
平行线的性质
平行线的判定与性质
【解析】
如图，过A点作a′//b .
∵ ∠3=∠1时， a′//b，
∵ ∠1=67∘，
∴ ∠3=67∘，
∴ ∠2=180∘−∠3=113∘，
故答案为： 113∘ .
【解答】
解：如图，过A点作a′//b ，
当∠3=∠1=67∘时， a′//b，
则∠2=180∘−∠3=113∘.
故答案为： 113∘ .
【答案】
1200
【考点】
扇形统计图
【解析】
根据统计扇形图我们可知小明一家在购物上用去了总支出的25%，因此让总支出乘以25%就可得到他们在购物上的支出．
【解答】
解：∵ 小明一家支出分为三种即路费、食宿和购物，且路费、食宿占了75%，
∴ 购物占总支出的1−75%=25%，
∴ 总购物支出为4800×25%=1200（元）.
故答案为：1200.
【答案】
2≤a<3
【考点】
一元一次不等式的整数解
【解析】
由不等式x−1≤a得x≤a+1，根据不等式有四个非负整数解知3≤a+1<4，求解可得．
【解答】
解：解不等式x−1≤a，解得x≤a+1.
∵ 不等式有四个非负整数解，
∴ 3≤a+1<4，
解得2≤a<3.
故答案为：2≤a<3.
【答案】
2
【考点】
根与系数的关系
一元二次方程的解
【解析】
根据根与系数的关系求解．
【解答】
解：∵ x1，x2是一元二次方程x2−4x−7=0的两个实数根，
∴ x1+x2=4，x1x2=−7，
∴ x12+4x1x2+x22=(x1+x2)2+2x1x2=16−14=2.
故答案为：2.
【答案】
11
【考点】
解直角三角形的应用-方向角问题
勾股定理的应用
【解析】
根据正弦和余弦的定义计算即可．
【解答】
解：如图：
在Rt△APC中，PC=AP×cs∠APC=9，
在Rt△PCB中，PB=PCsin∠B≈11（海里），
故答案为：11.
【答案】
12
【考点】
解分式方程
【解析】
首先根据题意可得到方程：16−1x=14−16，然后解分式方程，把分式的两边乘以最简公分母12x去分母，然后去括号，移项，合并同类项，把x的系数化为1，最后一定要检验．
【解答】
解：根据题意，得16−1x=14−16，
去分母，得2x−12=3x−2x，
移项，得2x+2x−3x=12，
合并同类项，得x=12．
检验，把x=12代入最简公分母12x≠0，
故原分式方程的解为x=12．
故答案为：12．
【答案】
(2019+6733, 0)
【考点】
规律型：点的坐标
坐标与图形变化-旋转
勾股定理
【解析】
根据勾股定理列式求出AB的长，再根据第四个三角形与第一个三角形的位置相同可知每三个三角形为一个循环组依次循环，然
后求出一个循环组旋转前进的长度，再用2019除以3，根据商为673可知第2019个三角形的直角顶点为循环组的最后一个三角形
的顶点，求出即可．
【解答】
解：由题意，得点A−1,0，B0,3，
则AB=12+32=2，
由图可知，每三个三角形为一个循环组依次循环，
且一个循环组前进的长度为3+2+1=3+3，
又2019÷3=673，
则△2019的直角顶点是第673个循环组的最后一个三角形的直角顶点，
673×3+3=2019+6733，
所以△2019 的直角顶点的坐标为2019+6733,0.
故答案为：2019+6733,0.
三、解答题
【答案】
解：原式=3−1−4×32+6
=3−1−23+6
=−3+5.
【考点】
特殊角的三角函数值
零指数幂、负整数指数幂
实数的运算
绝对值
【解析】
原式=3−1−4×32+6
=3−1−23+6
=−3+5 .
【解答】
解：原式=3−1−4×32+6
=3−1−23+6
=−3+5.
【答案】
(1)证明：∵ △ABC是等边三角形，
∴ AB=AC，∠BAC=∠C=60∘.
在△ABE与△CAD中，
AB=AC,∠BAC=∠C,AE=CD,
∴ △ABE≅△CAD(SAS).
(2)由(1)得△ABE≅△CAD，
∴ ∠ABE=∠CAD，
∴ ∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP
=∠BAC=60∘.
∵ BQ⊥AD，
∴ ∠PBQ=90∘−∠BPQ=30∘.
【考点】
等边三角形的性质
全等三角形的判定
全等三角形的性质
【解析】
（1）根据等边三角形的性质可得AB=AC，∠BAC=∠C=60∘，然后利用“边角边”即可证明两三角形；
（2）由SAS可得△ABE≅△CAD，进而得出对应角相等，再通过角之间的转化即可求解∠BPD的度数，进而求得结论．
【解答】
(1)证明：∵ △ABC是等边三角形，
∴ AB=AC，∠BAC=∠C=60∘.
在△ABE与△CAD中，
AB=AC,∠BAC=∠C,AE=CD,
∴ △ABE≅△CAD(SAS).
(2)由(1)得△ABE≅△CAD，
∴ ∠ABE=∠CAD，
∴ ∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP
=∠BAC=60∘.
∵ BQ⊥AD，
∴ ∠PBQ=90∘−∠BPQ=30∘.
【答案】
解：(1)由题意得，列表如下：
则共有16种等可能的结果.
(2)∵ 这样的点落在直线y=5−x上的有
(1, 4)，(2, 3)，(3, 2)，(4, 1)，
∴ 这样的点落在直线y=5−x上的概率为416=14.
【考点】
列表法与树状图法
概率公式
【解析】
(1)首先根据题意列出表格，然后由表格即可求得所有等可能的结果；
(2)根据(1)中的表格求得这样的点落在直线y=5−x上的情况，然后利用概率公式求解即可求得答案．
【解答】
解：(1)由题意得，列表如下：
则共有16种等可能的结果.
(2)∵ 这样的点落在直线y=5−x上的有
(1, 4)，(2, 3)，(3, 2)，(4, 1)，
∴ 这样的点落在直线y=5−x上的概率为416=14.
【答案】
解：(1)把A(a, −2)代入y=12x，可得a=−4，
∴ A(−4, −2).
把A(−4, −2)代入y=kx，可得k=8，
∴ 反比例函数的表达式为y=8x，
∵ 点B与点A关于原点对称，
∴ B(4, 2).
(2)如图所示，过P作PE⊥x轴于E，交AB于C，
设P(m, 8m)，则C(m, 12m)，
∵ △POC的面积为3，
∴ 12m×|12m−8m|=3，
解得m=27或2，
∴ P(27, 477)或(2, 4)．
【考点】
三角形的面积
关于原点对称的点的坐标
反比例函数综合题
待定系数法求反比例函数解析式
【解析】
（1）把A(a, −2)代入y=12x，可得A(−4, −2)，把A(−4, −2)代入y=kx，可得反比例函数的表达式为y=8x，再根据点B与点A关于原点对称，即可得到B的坐标；
（2）过P作PE⊥x轴于E，交AB于C，先设P(m, 8m)，则C(m, 12m)，根据△POC的面积为3，可得方程12m×|12m−8m|＝3，求得m的值，即可得到点P的坐标．
【解答】
解：(1)把A(a, −2)代入y=12x，可得a=−4，
∴ A(−4, −2).
把A(−4, −2)代入y=kx，可得k=8，
∴ 反比例函数的表达式为y=8x，
∵ 点B与点A关于原点对称，
∴ B(4, 2).
(2)如图所示，过P作PE⊥x轴于E，交AB于C，
设P(m, 8m)，则C(m, 12m)，
∵ △POC的面积为3，
∴ 12m×|12m−8m|=3，
解得m=27或2，
∴ P(27, 477)或(2, 4)．
【答案】
解：(1)设A种树苗每棵x元，B种树苗每棵y元，
根据题意，得8x+3y=950,5x+6y=800,
解得x=100,y=50.
答：A种树苗每棵100元，B种树苗每棵50元.
(2)设购进A种树苗m棵，则购进B种树苗(100−m)棵，
根据题意，得m≥52,100−m≥0,100m+50(100−m)≤7650,
解得52≤m≤53，
所以购买的方案有两种：
①购进A种树苗52棵，B种树苗48棵；
②购进A种树苗53棵，B种树苗47棵.
(3)方案①的费用为52×30+48×20=2520（元），
方案②的费用为53×30+47×20=2530（元），
所以购进A种树苗52棵，B种树苗48棵所付工钱最少，最少工钱为2520元.
【考点】
二元一次方程组的应用——其他问题
一元一次不等式组的应用
【解析】
（1）设A种树苗每棵x元，B种树苗每棵y元，根据“购买A种树苗8棵，B种树苗3棵，需要950元；若购买A种树苗5棵，B种树苗6棵，则需要800元”列二元一次方程组求解可得；
（2）设购进A种树苗m棵，则购进B种树苗(100−m)棵，根据“A种树苗不能少于52棵，且用于购买这两种树苗的资金不能超过7650元”列不等式组求解可得；
（3）根据（2）中所得方案，分别计算得出费用即可．
【解答】
解：(1)设A种树苗每棵x元，B种树苗每棵y元，
根据题意，得8x+3y=950,5x+6y=800,
解得x=100,y=50.
答：A种树苗每棵100元，B种树苗每棵50元.
(2)设购进A种树苗m棵，则购进B种树苗(100−m)棵，
根据题意，得m≥52,100−m≥0,100m+50(100−m)≤7650,
解得52≤m≤53，
所以购买的方案有两种：
①购进A种树苗52棵，B种树苗48棵；
②购进A种树苗53棵，B种树苗47棵.
(3)方案①的费用为52×30+48×20=2520（元），
方案②的费用为53×30+47×20=2530（元），
所以购进A种树苗52棵，B种树苗48棵所付工钱最少，最少工钱为2520元.
【答案】
(1)证明：如图，连接OA，设AB与CD交于点F，
∵ ⊙O为等边△ABC的外接圆，D为直径CE延长线上的一点，
∴ ∠ACD=12∠ACB=30∘，CD⊥AB，
∵ AD=AC，
∴ ∠D=∠ACD=30∘，
∴ ∠DAC=180∘−30∘−30∘=120∘，
∵ OA=OC，
∴ ∠OAC=∠ACD=30∘，
∴ ∠OAD=120∘−30∘=90∘，
∴ AD⊥OA，
∴ AD是⊙O的切线.
(2)解：由(1)可知，CD⊥AB，∠D=30∘，
∵ AD=AC，
∴ DF=CF=12CD=3，
∴ AF=33DF=3，
∴ AD=2AF=23，
∵ ∠OAD=90∘, ∠D=30∘，
∴ ∠AOD=60∘，
∴ OA=33AD=2，
∴ S阴影=S△OAD−S扇形AOE
=12×2×23−60∘×π×22360∘=23−23π.
【考点】
等边三角形的性质
三角形的外接圆与外心
切线的判定
等腰梯形的性质
锐角三角函数的定义
扇形面积的计算
求阴影部分的面积
【解析】
（1）连接OA，由等边三角形的性质得出∠ACD = 12∠ACB＝30∘，CD⊥AB，由等腰三角形的性质得出∠D＝∠ACD＝30∘，求出∠DAC＝120∘，∠OAC＝∠ACD＝30∘，得出∠OAD＝90∘，即可得出结论；
（2）由等腰三角形的性质和直角三角形的性质求出DF＝CF = 12CD＝3，AD＝2AF＝23，OA = 33AD＝2，阴影部分的面积＝△OAD的面积-扇形AOE的面积，由三角形面积公式和扇形面积公式即可得出答案．
【解答】
(1)证明：如图，连接OA，设AB与CD交于点F，
∵ ⊙O为等边△ABC的外接圆，D为直径CE延长线上的一点，
∴ ∠ACD=12∠ACB=30∘，CD⊥AB，
∵ AD=AC，
∴ ∠D=∠ACD=30∘，
∴ ∠DAC=180∘−30∘−30∘=120∘，
∵ OA=OC，
∴ ∠OAC=∠ACD=30∘，
∴ ∠OAD=120∘−30∘=90∘，
∴ AD⊥OA，
∴ AD是⊙O的切线.
(2)解：由(1)可知，CD⊥AB，∠D=30∘，
∵ AD=AC，
∴ DF=CF=12CD=3，
∴ AF=33DF=3，
∴ AD=2AF=23，
∵ ∠OAD=90∘, ∠D=30∘，
∴ ∠AOD=60∘，
∴ OA=33AD=2，
∴ S阴影=S△OAD−S扇形AOE
=12×2×23−60∘×π×22360∘=23−23π.
【答案】
解：(1)根据题意可设：y=a(x−4)2−16，
当x=10时，y=20，
所以a(10−4)2−16=20，
解得a=1，
所以函数关系式为y=(x−4)2−16．
(2)当x=9时，y=(9−4)2−16=9，
所以前9个月公司累计获得的利润为9万元.
由题意可知，当x=10时，y=20，
因为20−9=11，
所以10月份一个月内所获得的利润11万元．
(3)设在前12个月中，第n个月该公司一个月内所获得的利润为s（万元），
则s=(n−4)2−16−[(n−1−4)2−16]=2n−9，
因为s是关于n的一次函数，且2>0，
所以s随着n的增大而增大。
因为n的最大值为12，
所以当n=12时，smax=15，
所以第12月份该公司一个月内所获得的利润最多，最多利润是15万元．
【考点】
二次函数的应用
【解析】
(1)根据题意此抛物线的顶点坐标为(4, −16)，设出抛物线的顶点式，把(10, 20)代入即可求出a的值，把a的值代入抛物线的顶点式中即可确定出抛物线的解析式；
(2)相邻两个月份的总利润的差即为某月利润．
(3)根据前x个月内所获得的利润减去前x−1个月内所获得的利润，再减去16即可表示出第x个月内所获得的利润，为关于x的一次函数，且为增函数，得到x取最大为12时，把x=12代入即可求出最多的利润．
【解答】
解：(1)根据题意可设：y=a(x−4)2−16，
当x=10时，y=20，
所以a(10−4)2−16=20，
解得a=1，
所以函数关系式为y=(x−4)2−16．
(2)当x=9时，y=(9−4)2−16=9，
所以前9个月公司累计获得的利润为9万元.
由题意可知，当x=10时，y=20，
因为20−9=11，
所以10月份一个月内所获得的利润11万元．
(3)设在前12个月中，第n个月该公司一个月内所获得的利润为s（万元），
则s=(n−4)2−16−[(n−1−4)2−16]=2n−9，
因为s是关于n的一次函数，且2>0，
所以s随着n的增大而增大。
因为n的最大值为12，
所以当n=12时，smax=15，
所以第12月份该公司一个月内所获得的利润最多，最多利润是15万元．
【答案】
解：(1)由题意：16a+c=0，4a+c=94，
解得a=−316，c=3，
∴ 抛物线的解析式为y=−316(x−2)2+3，
∴ 顶点D坐标(2, 3)．
(2)可能．
∵ A(−2, 0)，D(2, 3)，根据抛物线性质知点B(6, 0)，
∴ AB=8，AD=BD=5.
①当DE=DF时，∠DFE=∠DEF=∠DAB=∠ABD，
∴ EF // AB，此时E与A重合，与条件矛盾，不成立.
②当DE=EF时，
∵ ∠DEF=∠DAB,
∠DAB+∠AED+∠ADE=180∘，
∠AED+∠DEF+∠FEB=180∘，
∴ ∠ADE=∠FEB.
又∵ ∠DAB=∠ABD，
∴ △BEF∽△ADE.
又DE=EF，
∴ △BEF≅△ADE，
∴ BE=AD=5.
③当DF=EF时，∠EDF=∠DEF=∠DAB=∠DBA，
∴ △FDE∽△DAB，
∴ EFBD=DEAB，
∴ EFDE=BDAB=58.
∵ △BEF∽△ADE，
∴ EBAD=EFDE=58，
∴ EB=58AD=258.
故当BE的长为5或258时，△DEF为等腰三角形．
(3)如图，连接BD，当点P在线段BD的右侧时，作DH⊥AB于H，
连接PD，PH，PB．
设P(n, −316(n−2)2+3)，
则S△PBD=S△PBH+S△PDH−S△BDH
=12×4×[−316(n−2)2+3]+12×3×(n−2)−12×4×3
=−38(n−4)2+32.
∵ −38<0，
∴ 当n=4时，△PBD的面积最大值为32.
由题意知，S△CBD=92.
∵ S△PBDS△CBD=m，
∴ 当点P在BD的右侧时，m的最大值=3292=13.
观察图象可知：当0当m=13时，满足条件的点P的个数有3个，
当m>13时，满足条件的点P的个数有2个（此时点P在BD的左侧）．
【考点】
等腰三角形的性质与判定
相似三角形的性质与判定
全等三角形的性质与判定
二次函数综合题
待定系数法求二次函数解析式
二次函数图象上点的坐标特征
【解析】
(1)利用待定系数法，转化为解方程组即可解决问题．
(2)可能．分三种情形①当DE=DF时；②当DE=EF时；③当DF=EF时，分别求解即可．
(3)如图，连接BD，当点P在线段BD的右侧时，作DH⊥AB于H，连接PD，PH，PB．设P(n, −316(n−2)2+3)，构建二次函数求出△PBD的面积最大值，再根据对称性即可解决问题．
【解答】
解：(1)由题意：16a+c=0，4a+c=94，
解得a=−316，c=3，
∴ 抛物线的解析式为y=−316(x−2)2+3，
∴ 顶点D坐标(2, 3)．
(2)可能．
∵ A(−2, 0)，D(2, 3)，根据抛物线性质知点B(6, 0)，
∴ AB=8，AD=BD=5.
①当DE=DF时，∠DFE=∠DEF=∠DAB=∠ABD，
∴ EF // AB，此时E与A重合，与条件矛盾，不成立.
②当DE=EF时，
∵ ∠DEF=∠DAB,
∠DAB+∠AED+∠ADE=180∘，
∠AED+∠DEF+∠FEB=180∘，
∴ ∠ADE=∠FEB.
又∵ ∠DAB=∠ABD，
∴ △BEF∽△ADE.
又DE=EF，
∴ △BEF≅△ADE，
∴ BE=AD=5.
③当DF=EF时，∠EDF=∠DEF=∠DAB=∠DBA，
∴ △FDE∽△DAB，
∴ EFBD=DEAB，
∴ EFDE=BDAB=58.
∵ △BEF∽△ADE，
∴ EBAD=EFDE=58，
∴ EB=58AD=258.
故当BE的长为5或258时，△DEF为等腰三角形．
(3)如图，连接BD，当点P在线段BD的右侧时，作DH⊥AB于H，
连接PD，PH，PB．
设P(n, −316(n−2)2+3)，
则S△PBD=S△PBH+S△PDH−S△BDH
=12×4×[−316(n−2)2+3]+12×3×(n−2)−12×4×3
=−38(n−4)2+32.
∵ −38<0，
∴ 当n=4时，△PBD的面积最大值为32.
由题意知，S△CBD=92.
∵ S△PBDS△CBD=m，
∴ 当点P在BD的右侧时，m的最大值=3292=13.
观察图象可知：当0当m=13时，满足条件的点P的个数有3个，
当m>13时，满足条件的点P的个数有2个（此时点P在BD的左侧）．甲
乙
丙
丁
平均数（cm）
185
180
185
180
方差
3.6
4.6
5.4
6.1
第一次
第二次
1
2
3
4
1
(1, 1)
(2, 1)
(3, 1)
(4, 1)
2
(1, 2)
(2, 2)
(3, 2)
(4, 2)
3
(1, 3)
(2, 3)
(3, 3)
(4, 3)
4
(1, 4)
(2, 4)
(3, 4)
(4, 4)
第一次第二次
1
2
3
4
1
(1, 1)
(2, 1)
(3, 1)
(4, 1)
2
(1, 2)
(2, 2)
(3, 2)
(4, 2)
3
(1, 3)
(2, 3)
(3, 3)
(4, 3)
4
(1, 4)
(2, 4)
(3, 4)
(4, 4)