2020-2021学年湖北省麻城市某校初三（下）4月月考数学试卷

这是一份2020-2021学年湖北省麻城市某校初三（下）4月月考数学试卷，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


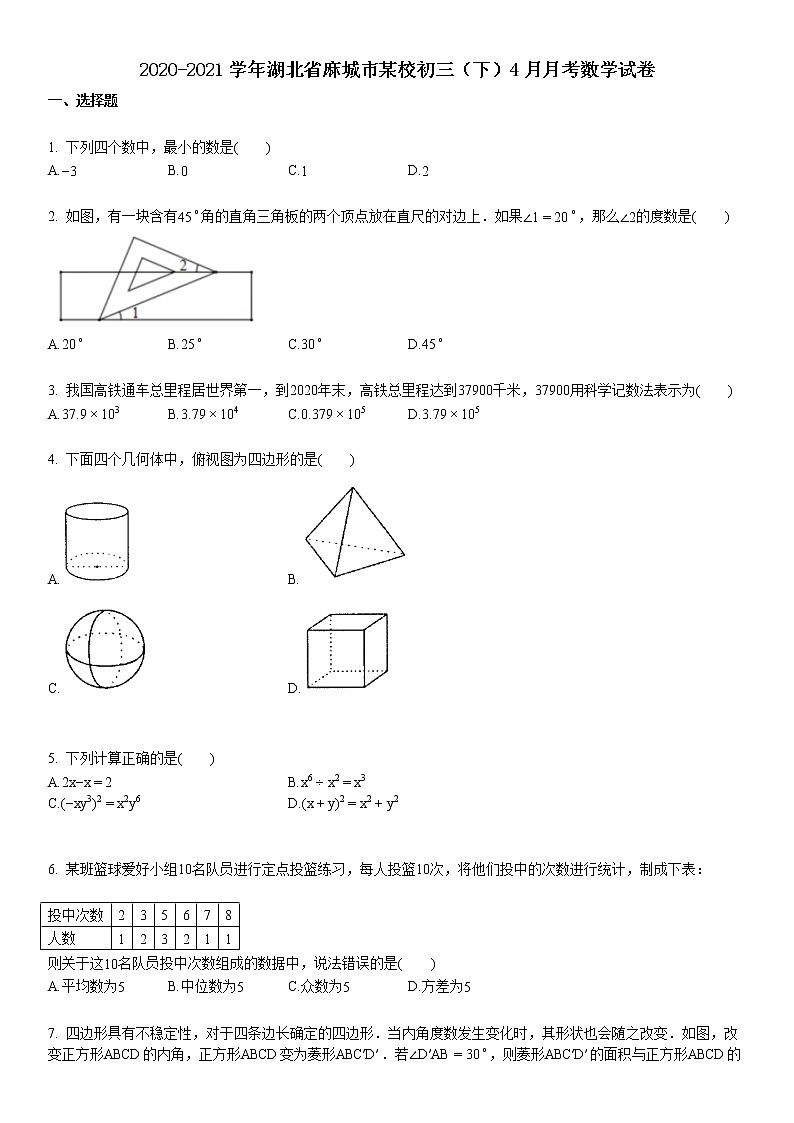
1. 下列四个数中，最小的数是( )
A.−3B.0C.1D.2

2. 如图，有一块含有45∘角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20∘，那么∠2的度数是( )

A.20∘B.25∘C.30∘D.45∘

3. 我国高铁通车总里程居世界第一，到2020年末，高铁总里程达到37900千米，37900用科学记数法表示为( )
A.37.9×103×104×105×105

4. 下面四个几何体中，俯视图为四边形的是( )
A.B.
C.D.

5. 下列计算正确的是( )
A.2x−x=2B.x6÷x2=x3
C.(−xy3)2=x2y6D.(x+y)2=x2+y2

6. 某班篮球爱好小组10名队员进行定点投篮练习，每人投篮10次，将他们投中的次数进行统计，制成下表：
则关于这10名队员投中次数组成的数据中，说法错误的是( )
A.平均数为5B.中位数为5C.众数为5D.方差为5

7. 四边形具有不稳定性，对于四条边长确定的四边形．当内角度数发生变化时，其形状也会随之改变．如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC′D′．若∠D′AB=30∘，则菱形ABC′D′的面积与正方形ABCD的面积之比是( )

A.12B.22C.32D.1

8. 如图，在△ABC中，AC=BC，∠ACB=90∘，AB=2．动点P沿AB从点A向点B移动，过点P作AB的垂线，交折线ACB于点Q．记AP=x，△APQ的面积为y，则y关于x的函数图像大致是( )

A.B.
C.D.
二、填空题

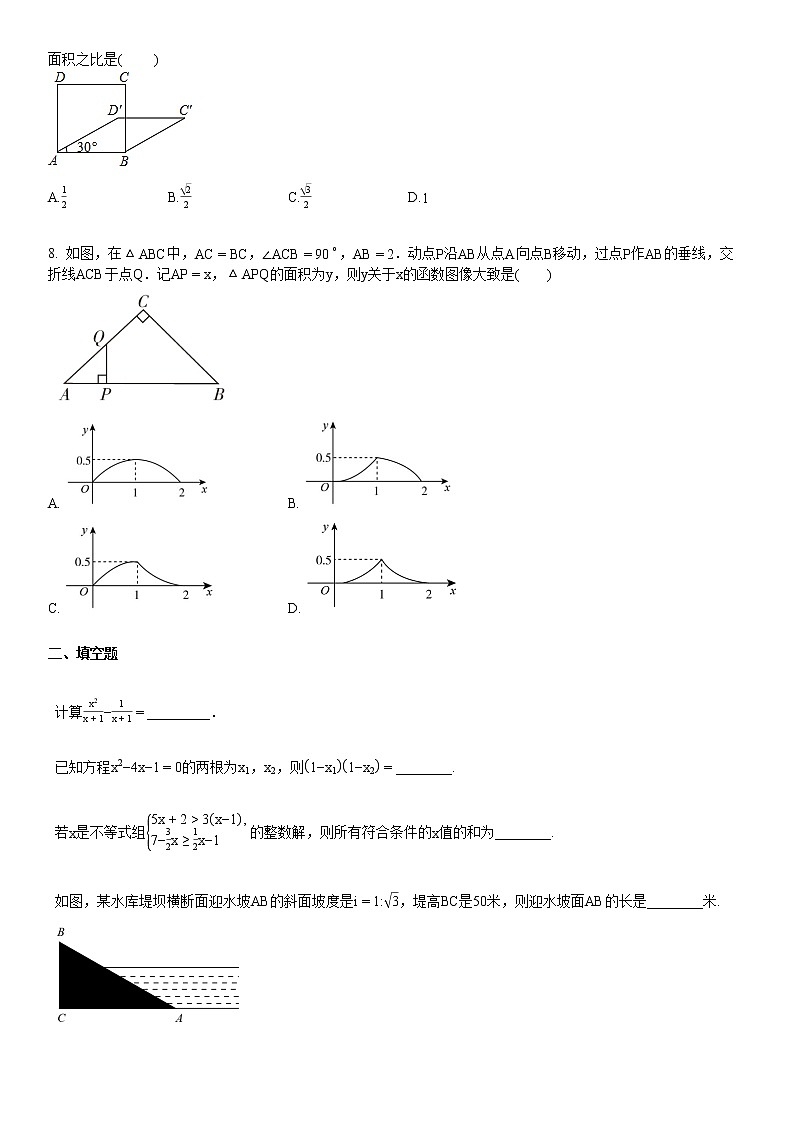
计算x2x+1−1x+1=_________．

已知方程x2−4x−1=0的两根为x1，x2，则1−x11−x2=________.

若x是不等式组5x+2>3x−1,7−32x≥12x−1 的整数解，则所有符合条件的x值的和为________.

如图，某水库堤坝横断面迎水坡AB的斜面坡度是i=1:3，堤高BC是50米，则迎水坡面AB的长是________米.


中华文化源远流长，《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表，被称为“四大古典名著”．孝咸中学为了了解学生在寒假期间对四大古典名著的阅读情况，就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查，根据调查结果绘制成如图不完整的两幅统计图：
根据以上信息，本次调查所得数据中，扇形统计图中“读完了4部”所在扇形的圆心角为________度.

如图，在Rt△ABC中，∠ABC=90∘，AB=1，BC=12．进行如下操作：
①以点C为圆心，以BC的长为半径画弧交AC于点D；
②以点A为圆心，以AD的长为半径画弧交AB于点E．
根据以上作图步骤，则AE的长为________.


我国古代数学家杨辉发现了如图所示的三角形，我们称之为“杨辉三角”，它具有一定的规律性，从图中取一列数：1，3，6，10，⋯，分别记为a1=1，a2=3，a3=6，a4=10，⋯，那么1a1+1a2+1a3+⋯+1a10的值是________.


如图，在Rt△ABC中，∠ACB=90∘，点D为AB的中点，将△ACD沿CD折叠得到△ECD，连接BE．若CA=1，CB=2，则线段BE=________.

三、解答题

计算:8+13−2−|1−2|−2cs45∘.

已知：如图，AB=DC，AC=DB，AC和BD相交于点O，点E是BC的中点，连接OE．

(1)求证：△ABC≅△DCB；

(2)求∠BEO的度数．

将背面相同，正面分别标有数字1，2，3，4的四张卡片洗匀后，背面朝上放在桌面上．
(1)从中随机抽取一张卡片，求该卡片正面上的数字是偶数的概率；

(2)先从中随机抽取一张卡片（不放回），将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，则组成的两位数恰好是4的倍数的概率是多少？请用树状图或列表法加以说明．

已知：如图，反比例函数y=kx(k≠0)与一次函数y=−x+b的图象在第一象限交于点A(1, 3)，点B(3, 1).
(1)求反比例函数和一次函数的解析式；

(2)已知点P(a, 0)(a>0)，过点P作平行于y轴的直线，在第一象限内交一次函数y=−x+b的图象于点M，交反比例函数y=kx的图象于点N．若PM>PN，结合函数图象直接写出a的取值范围．

已知：如图，AB为⊙O的直径，点C为⊙O上一点，∠ACB的平分线与⊙O交于点D，与AB交于点E．点F为DC的延长线上一点，满足∠FBC=∠BDC．

(1)求证：BF与⊙O相切；

(2)若BD=6，BC=22，求AC的值．

某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎，每扎1000张，已知体彩中心有A，B，C三种不同价格的彩票，进价分别是A彩票每张1.5元，B彩票每张2元，C彩票每张2.5元．
(1)若经销商同时购进两种不同型号的彩票20扎，用去45000元，请你设计进票方案；

(2)若销售A型彩票一张获手续费0.2元，B型彩票一张获手续费0.3元，C型彩票一张获手续费0.5元．在购进两种彩票的方案中，为使销售完时获得手续费最多，你选择哪种进票方案？

(3)若经销商准备用45000元同时购进A，B，C三种彩票20扎，请你设计进票方案．

红星企业加大技术创新，研发出一种新产品，对新产品的生产和销售进行了规划．从2021年1月开始生产并销售该种产品，该种产品的生产成本为6万元/件，设第x（1≤x≤12，且x为整数）月份该种产品的售价为y万元/件，y与x之间的函数关系如图所示．

(1)直接写出y与x之间的函数解析式，并写出自变量x的取值范围；

(2)第x月份生产并销售的产品数量为z件，z=2x+8（1≤x≤12，且x为整数）．该企业在第几月份所获的月利润最大？最大月利润为多少万元？

已知：抛物线y=x2+bx+c经过点A−1,0和点C0,−3，与x轴交于另一点B．
(1)求抛物线的解析式；

(2)点P为第四象限内抛物线上的点，连接CP，AP，AC，设点P的横坐标为m0①如图1，当CP⊥AC时，求tan∠PAB的值；
②如图2，连接AC，过点P作x轴的垂线，垂足为点D，过点C作AP的垂线，与射线PD交于点E，与x轴交于点F．当∠EAD=∠ACO时，求m的值．
参考答案与试题解析
2020-2021学年湖北省麻城市某校初三（下）4月月考数学试卷
一、选择题
1.
【答案】
A
【考点】
有理数大小比较
【解析】
根据有理数的大小比较方法，找出最小的数即可．
【解答】
解：由有理数比较大小的方法可知，2>1>0>−3，
故四个数中，最小的数是−3．
故选A．
2.
【答案】
B
【考点】
平行线的性质
【解析】
根据两直线平行，内错角相等求出∠3，再求解即可．
【解答】
解：如图，
∵直尺的上下两边平行，∠1=20∘，
∴∠3=∠1=20∘，
∴∠2=45∘−20∘=25∘．
故选B．
3.
【答案】
B
【考点】
科学记数法--表示较大的数
【解析】
此题暂无解析
【解答】
解：37900=3.79×104.
故选B.
4.
【答案】
D
【考点】
简单几何体的三视图
【解析】
根据俯视图的定义分析即可解答.
【解答】
解：A，该几何体的俯视图是圆，故A错误；
B，该几何体的俯视图是三角形，故B错误；
C，该几何体的俯视图是圆，故C错误；
D，该几何体的俯视图是四边形，故D正确.
故选D.
5.
【答案】
C
【考点】
同底数幂的除法
幂的乘方与积的乘方
完全平方公式
合并同类项
【解析】
根据同底数幂的除法，合并同类项法则，积的乘方和完全平方公式求出每个式子的值，再判断即可．
【解答】
解：A，2x−x=x，故本选项错误；
B，x6÷x2=x6−2=x4，故本选项错误；
C，(−xy3)2=x2y6，故本选项正确；
D，(x+y)2=x2+2xy+y2，故本选项错误.
故选C.
6.
【答案】
D
【考点】
算术平均数
中位数
众数
方差
【解析】
根据定义求出这组数据的平均数、中位数和众数、方差，根据结果即可选出正确的一项.
【解答】
解：A，因为x=2×1+3×2+5×3+6×2+7×1+8×11+2+3+2+1+1=5，故A正确；
B，因为把这一组数据按从小到大的顺序排列后，处在最中间位置的两个数都是5，所以中位数是5，故B正确；
C，因为在这一组数据中5出现了3次，出现的次数最多，所以众数是5，故C正确；
D，因为s2=1102−52+3−52+⋯+7−52+8−52=2.7，故D错误.
故选D.
7.
【答案】
A
【考点】
含30度角的直角三角形
菱形的面积
正方形的性质
【解析】
根据30∘角所对的直角边等于斜边的一半可知菱形ABC′D′的高等于AB的一半，再根据正方形的面积公式和平行四边形的面积公式即可得解．
【解答】
解：根据题意可知菱形ABC′D′的高等于AB的一半，
∴ 菱形ABC′D′的面积为12AB2，正方形ABCD的面积为AB2．
∴ 菱形ABC′D′的面积与正方形ABCD的面积之比是12．
故选A.
8.
【答案】
B
【考点】
等腰三角形的性质
函数的图象
根据实际问题列二次函数关系式
【解析】
过点C作CD⊥AB，垂足为D，然后求出y与x之间的函数关系式，最后根据关系式即可选出正确的一项.
【解答】
解：如图，过点C作CD⊥AB，垂足为D.
∵AC=BC，∠ACB=90∘，AB=2，
∴ ∠A=∠B=45∘，AD=CD=BD=1.
∵QP⊥AB，
∴AP=QP=x，
∴当点P在点D的左侧时，y=12x20≤x≤1；
当点P在点D的右侧时，y=12x2−x=−12x2+x1根据函数的解析式可知只有B正确.
故选B.
二、填空题
【答案】
x−1
【考点】
分式的加减运算
【解析】
根据分式的减法和除法法则以及平方差公式可得.
【解答】
解：x2x+1−1x+1
=x2−1x+1
=(x+1)(x−1)x+1
=x−1.
故答案为：x−1.
【答案】
−4
【考点】
根与系数的关系
多项式乘多项式
【解析】
根据一元二次方程根与系数的关系可得x1+x2=4，x1⋅x2=−1，然后根据多项式乘多项式计算1−x11−x2，再把x1+x2=4，x1⋅x2=−1代入计算即可.
【解答】
解：∵ x1，x2是方程x2−4x−1=0的两个根，
∴ x1+x2=4，x1⋅x2=−1.
∴ 1−x11−x2
=1−x1−x2+x1⋅x2
=1−x1+x2+x1⋅x2
=1−4−1
=−4.
故答案为：−4.
【答案】
7
【考点】
一元一次不等式组的整数解
【解析】
先求出不等式组的解集，得到整数解，再求和即可.
【解答】
解：5x+2>3x−1①，7−32x≥12x−1②，
解不等式①得： 5x+2>3x−3，
2x>−5，
x>−52 ，
解不等式②得： −32x−12x≥−1−7，
−2x≥−8，
x≤4，
∴ 不等式组的解集为 −52∵ x是不等式组的整数解，
∴ x可取−2，−1，0，1，2，3，4，
∴−2+−1+0+1+2+3+4=7 ，
所有符合条件的x值的和为7.
故答案为：7.
【答案】
100
【考点】
解直角三角形的应用-坡度坡角问题
含30度角的直角三角形
【解析】
首先根据坡度求出∠BAC=30∘，然后根据直角三角形的性质即可求出AB的长.
【解答】
解：∵ 迎水坡AB的斜面坡度是i=1:3，
∴ tan∠BAC=13=33，
∴ ∠BAC=30∘，
∴ AB=2BC=2×50=100（米）.
故答案为：100.
【答案】
72∘
【考点】
扇形统计图
条形统计图
【解析】
用360∘乘以4部人数所占比例即可.
【解答】
解：本次调查的总人数为10÷25%=40（人），
由条形图知“4部”的有8人，
所以扇形统计图中“读完了4部”所在扇形的圆心角为360∘×840=72∘.
故答案为：72∘.
【答案】
5−12
【考点】
勾股定理
作图—尺规作图的定义
【解析】
此题暂无解析
【解答】
解：∵∠ABC=90∘，
∴AC2=AB2+BC2 =12+122=54，
∴AC=52.
∵BC=12，
∴CD=BC=12，
∴AD=AE=AC−CD=52−12 =5−12.
故答案为：5−12.
【答案】
2011
【考点】
有理数的加法
规律型：数字的变化类
【解析】
根据已知条件找出规律：an=nn+12，再计算即可.
【解答】
解： ∵a1=1 ，a2=3， a3=6 ，a4=10，⋯，
可得出an=nn+12，
∴ 1a1+1a2+1a3+⋯+1a10
=21×2+22×3+23×4+⋯+210×11
=2×11×2+12×3+13×4+⋯+110×11
=2×1−12+12−13+13−14+⋯+110−111
=2×1−111
=2×1011
=2011.
故答案为： 2011.
【答案】
355
【考点】
翻折变换（折叠问题）
勾股定理
三角形中位线定理
【解析】
利用翻折变换（折叠问题）性质解题
【解答】
解：连接AE，设AE与CD交于点O，如图，
由折叠性质可知，DC⊥AE，且 AO= EO，
又∵ AC=1，BC=2，∠BCA=90∘，
∴ AB=BC2+AC2=12+22 =5.
又∵ D是AB的中点，∴ CD=AD=BD= 52.
设DO=a，则CO=DC−DO= 52−a.
又∵ AD2−DO2=AO2， CA2−CO2=AO2，
∴ AD2−DO2=CA2−CO2，即522−a2=12−52−a2，
解得a=3510，
即OD=3510.
又∵ BD=AD，EO=AO，
∴ OD=12BE(三角形中位线定理)，
∴ BE=2OD=2×3510=355.
故答案为：355.
三、解答题
【答案】
解：原式=22+9−2−1−2×22
=22+9−2+1−2
=10．
【考点】
算术平方根
零指数幂、负整数指数幂
实数的运算
绝对值
特殊角的三角函数值
【解析】
此题暂无解析
【解答】
解：原式=22+9−2−1−2×22
=22+9−2+1−2
=10．
【答案】
(1)证明：在△ABC和△DCB中，
AB=DC,AC=DB,BC=CB,
∴ △ABC≅△DCB.
(2)解：∵ △ABC≅△DCB，
∴ ∠ACB=∠DBC，∴ OB=OC.
∵ E是BC的中点，
∴ ∠BEO=∠CEO=12∠BEC=90∘.
【考点】
全等三角形的判定
全等三角形的性质
【解析】


【解答】
(1)证明：在△ABC和△DCB中，
AB=DC,AC=DB,BC=CB,
∴ △ABC≅△DCB.
(2)解：∵ △ABC≅△DCB，
∴ ∠ACB=∠DBC，∴ OB=OC.
∵ E是BC的中点，
∴ ∠BEO=∠CEO=12∠BEC=90∘.
【答案】
解：(1)从中随机抽取一张卡片有4种情况，抽到的卡片正面上的数字是偶数的有两种，
故P(偶数) =24=12.
(2)列表如下：
共有12种情况，其中恰好是4的倍数的有3种情况，
∴ P(4的倍数) =312=14．
【考点】
概率公式
列表法与树状图法
【解析】
无
无
【解答】
解：(1)从中随机抽取一张卡片有4种情况，抽到的卡片正面上的数字是偶数的有两种，
故P(偶数) =24=12.
(2)列表如下：
共有12种情况，其中恰好是4的倍数的有3种情况，
∴ P(4的倍数) =312=14．
【答案】
解：(1)∵ 反比例函数y=kx(k≠0)的图象与一次函数y=−x+b的图象在第一象限交于A(1, 3)，B(3, 1)两点，
∴ 3=k1，3=−1+b，
∴ k=3，b=4，
∴ 反比例函数和一次函数的表达式分别为y=3x，y=−x+4；
(2)由图象可得：当1PN．
【考点】
反比例函数与一次函数的综合
待定系数法求反比例函数解析式
待定系数法求一次函数解析式
【解析】
（1）利用待定系数法即可求得；
（2）根据图象可解．
【解答】
解：(1)∵ 反比例函数y=kx(k≠0)的图象与一次函数y=−x+b的图象在第一象限交于A(1, 3)，B(3, 1)两点，
∴ 3=k1，3=−1+b，
∴ k=3，b=4，
∴ 反比例函数和一次函数的表达式分别为y=3x，y=−x+4；
(2)由图象可得：当1PN．
【答案】
(1)证明：∵ AB为⊙O直径，
∴ ∠ACB=90∘，
∴ ∠CAB+∠CBA=90∘．
∵ ∠FBC=∠BDC，∠BDC=∠BAC，
∴ ∠FBC+∠CBA=90∘，
即∠FBA=90∘，
∴ BF⊥OB，
即BF与⊙O相切．
(2)解：如图，连接AD.
∵ CD平分△ACB，
∴ ∠ACD=∠BCD=45∘，
∴ ∠BAD=∠ABD=∠BCD=∠ACD=45∘，
∴ ∠ADB=90∘．
在Rt△ADB中，∵ BD=6，
∴ AB=BDsin∠BAD=6sin45∘=62，
∴ AC=AB2−BC2=622−222=8．
【考点】
圆周角定理
切线的判定
圆心角、弧、弦的关系
勾股定理
【解析】
无
无
【解答】
(1)证明：∵ AB为⊙O直径，
∴ ∠ACB=90∘，
∴ ∠CAB+∠CBA=90∘．
∵ ∠FBC=∠BDC，∠BDC=∠BAC，
∴ ∠FBC+∠CBA=90∘，
即∠FBA=90∘，
∴ BF⊥OB，
即BF与⊙O相切．
(2)解：如图，连接AD.
∵ CD平分△ACB，
∴ ∠ACD=∠BCD=45∘，
∴ ∠BAD=∠ABD=∠BCD=∠ACD=45∘，
∴ ∠ADB=90∘．
在Rt△ADB中，∵ BD=6，
∴ AB=BDsin∠BAD=6sin45∘=62，
∴ AC=AB2−BC2=622−222=8．
【答案】
解：(1)若设购进A种彩票x张，B种彩票y张，
根据题意，得x+y=1000×20,1.5x+2y=45000,
解得x=−10000，y=30000，
由于x<0，故不符合题意；
若设购进A种彩票x张，C种彩票y张，
根据题意，得x+y=1000×20,1.5x+2.5y=45000,
解得x=5000，y=15000；
若设购进B种彩票x张，C种彩票y张，
根据题意，得x+y=1000×20,2x+2.5y=45000,
解得x=10000，y=10000，
综上所述，若经销商同时购进两种不同型号的彩票共有两种方案可行，
即购买A种彩票5扎，C种彩票15扎或B种彩票与C种彩票各10扎.
(2)若购进A种彩票5扎，C种彩票15扎，
销售完后获手续费为0.2×5000+0.5×15000=8500（元）；
若购进B种彩票与C种彩票各10扎，
销售完后获手续费为0.3×10000+0.5×10000=8000（元），
所以为使销售完时获得手续最多选择的方案为A种彩票5扎，C种彩票15扎.
(3)若经销商准备用45000元同时购进A，B，C三种彩票20扎．
设购进A种彩票m扎，B种彩票n扎，C种彩票ℎ扎，
由题意，得m+n+ℎ=20，
1.5×1000m+2×1000n+2.5×1000ℎ=45000，
即ℎ=m+10，
所以n=−2m+10，
因为m，n都是正数，
所以1≤m<5，
又m为整数共有4种进票方案，具体如下：
方案1:A种1扎，B种8扎，C种11扎；
方案2:A种2扎，B种6扎，C种12扎；
方案3:A种3扎，B种4扎，C种13扎；
方案4:A种4扎，B种2扎，C种14扎．
【考点】
二元一次方程组的应用——销售问题
【解析】
（1）因为彩票有A，B，C三种不同型号，而经销商同时只购进两种，所以要将A，B，C两两组合，分三种情况：A，B；A，C；B，C，每种情况都可以根据下面两个相等关系列出方程，两种不同型号的彩票扎数之和＝20，购买两种不同型号的彩票钱数之和＝45000，然后根据实际含义确定他们的解．
（2）根据上一问分别求出每一种情况的手续费，然后进行比较，可以得出结果．
（3）有两个等量关系：A彩票扎数+B彩票扎数+C彩票扎数＝20，购买A彩票钱数+购买B彩票钱数+购买C彩票钱数＝45000．设三个未知数，用含有同一个未知数的代数式去表示另外的两个未知数，然后根据三个未知数的取值范围都小于20，得出一元一次不等式组，求出解集，最后根据实际含义确定解．
【解答】
解：(1)若设购进A种彩票x张，B种彩票y张，
根据题意，得x+y=1000×20,1.5x+2y=45000,
解得x=−10000，y=30000，
由于x<0，故不符合题意；
若设购进A种彩票x张，C种彩票y张，
根据题意，得x+y=1000×20,1.5x+2.5y=45000,
解得x=5000，y=15000；
若设购进B种彩票x张，C种彩票y张，
根据题意，得x+y=1000×20,2x+2.5y=45000,
解得x=10000，y=10000，
综上所述，若经销商同时购进两种不同型号的彩票共有两种方案可行，
即购买A种彩票5扎，C种彩票15扎或B种彩票与C种彩票各10扎.
(2)若购进A种彩票5扎，C种彩票15扎，
销售完后获手续费为0.2×5000+0.5×15000=8500（元）；
若购进B种彩票与C种彩票各10扎，
销售完后获手续费为0.3×10000+0.5×10000=8000（元），
所以为使销售完时获得手续最多选择的方案为A种彩票5扎，C种彩票15扎.
(3)若经销商准备用45000元同时购进A，B，C三种彩票20扎．
设购进A种彩票m扎，B种彩票n扎，C种彩票ℎ扎，
由题意，得m+n+ℎ=20，
1.5×1000m+2×1000n+2.5×1000ℎ=45000，
即ℎ=m+10，
所以n=−2m+10，
因为m，n都是正数，
所以1≤m<5，
又m为整数共有4种进票方案，具体如下：
方案1:A种1扎，B种8扎，C种11扎；
方案2:A种2扎，B种6扎，C种12扎；
方案3:A种3扎，B种4扎，C种13扎；
方案4:A种4扎，B种2扎，C种14扎．
【答案】
解：(1)由图可得，当1≤x≤8时，y=10，
当8可得10=8k+b,9=12k+b,解得k=−14,b=12,
所以当8所以函数解析式为 y=10(1≤x≤8,且x为整数）,−14x+12(8(2)设第x月的月利润为w万元，分两种情况：
①当1≤x≤8时， w=10−62x+8=8x+32 ，
∵ w随x的增大而增大，
∴ 当x=8时，w最大=8×8+32=96 （万元）.
②当8w=−14x+12−62x+8=−12x2+10x+48
=−12x−102+98，
∴ 当x=10时，w最大=98（万元） .
综上所述，该企业在第10月份所获的月利润最大，最大月利润为98万元．
【考点】
待定系数法求一次函数解析式
一次函数的应用
二次函数的应用
【解析】

【解答】
解：(1)由图可得，当1≤x≤8时，y=10，
当8可得10=8k+b,9=12k+b,解得k=−14,b=12,
所以当8所以函数解析式为 y=10(1≤x≤8,且x为整数）,−14x+12(8(2)设第x月的月利润为w万元，分两种情况：
①当1≤x≤8时， w=10−62x+8=8x+32 ，
∵ w随x的增大而增大，
∴ 当x=8时，w最大=8×8+32=96 （万元）.
②当8w=−14x+12−62x+8=−12x2+10x+48
=−12x−102+98，
∴ 当x=10时，w最大=98（万元） .
综上所述，该企业在第10月份所获的月利润最大，最大月利润为98万元．
【答案】
解：(1) ∵ y=x2+bx+c 经过A−1,0，C0,−3，
∴1−b+c=0,c=−3,
解得b=−2,c=−3,
∴ y=x2−2x−3.
(2)① 设直线AC的解析式为y=ax+b(a≠0)，
∵ A−1,0，C(0,−3)，
∴ −a+b=0,b=−3,
解得a=−3,b=−3,
∴ 直线AC的解析式为y=−3x−3.
又CP⊥AC，
∴ 可设直线CP的解析式为y=13x+n，
将C(0,−3)代入y=13x+n ，解得n=−3，
∴ y=13x−3 .
设点P的横坐标为m0∵ 点P在抛物线y=x2−2x−3上，也在直线y=13x−3 上，
∴ y=m2−2m−3,y=13m−3,
解得m=73或m=0（舍去），
∴ P73,−209，
∴ tan∠PAB=|yP||xP−xA|=20973+1=23 .
②∵ ∠EAD=∠ACO，且设点P的横坐标为m0∴ tan∠EAD=tan∠ACO=DEAD=OAOC=13，
∴ DE=13AD=131+m.
∵ CF⊥AP，PD⊥x轴，
∴ ∠APD=∠CFO.
又∵ ∠PDA=∠FOC=90∘ ，
∴ △APD∽△CFO，
∴ PDAD=OFOC，
∴ −m2−2m−3m+1=OF3，
∴ OF=9−3m，∴ F9−3m,0．
∵ F9−3m,0，C0,−3，
∴ 直线CF的解析式为y=13−mx−3，
∴ DE=|m3−m−3|=|4m−93−m|，
∴ |4m−93−m|=13m+1，
解得m=2或12或−5±55，
∵ 0∴ m=2或55−5.
【考点】
待定系数法求二次函数解析式
二次函数与一次函数的综合
二次函数图象与几何变换
两直线垂直问题
【解析】
根据待定系数法，将A−1,0, C0,−3代入二次函数解析式，求出b,c的值即可；
(2)①∵A−1,0，C(0,−3)，
设直线AC的解析式为y=ax+b，
∴−a+b=0,b=−3,
解得a=−3,b=−3,
∴直线AC的解析式为y=−3x−3.
又CP⊥AC，
∴可设直线CP的解析式为y=13x+n，
将C(0,−3)代入y=13x+n ，求得n=−3，
∴y=13x−3 .
∵点P在抛物线y=x2−2x−3上，也在直线y=13x−3 上，
∴y=x2−2x−3,y=13x−3,
解得x1=0，x2=73，
∴P73,−209，
∴ tan∠PAB=|yP||xP−xA|=20973+1=23 .
②
∵ ∠EAD=∠ACO，
∴ tan∠EAD=tan∠ACO=OAOC=13，
∴ DE=13AD=131+m.
∵ CF⊥AP，PD⊥x轴，
∴ ∠APD=∠CFO.
又∵ ∠PDA=∠FOC=90∘ ，
∴ △APD∽△CFO，
∴ PDAD=OFOC，
∴ −m2−2m−3m+1=OF3，
∴ OF=9−3m，∴ F9−3m,0．
∵ F9−3m,0，C0,−3，
∴ 直线CF的解析式为y=13−mx−3，
∴ DE=|m3−m−3|=|4m−93−m|，
∴ |4m−93−m|=13m+1，
解得m=2或12或−5±55.
∵ 0∴ m=2或55−5.
【解答】
解：(1) ∵ y=x2+bx+c 经过A−1,0，C0,−3，
∴1−b+c=0,c=−3,
解得b=−2,c=−3,
∴ y=x2−2x−3.
(2)① 设直线AC的解析式为y=ax+b(a≠0)，
∵ A−1,0，C(0,−3)，
∴ −a+b=0,b=−3,
解得a=−3,b=−3,
∴ 直线AC的解析式为y=−3x−3.
又CP⊥AC，
∴ 可设直线CP的解析式为y=13x+n，
将C(0,−3)代入y=13x+n ，解得n=−3，
∴ y=13x−3 .
设点P的横坐标为m0∵ 点P在抛物线y=x2−2x−3上，也在直线y=13x−3 上，
∴ y=m2−2m−3,y=13m−3,
解得m=73或m=0（舍去），
∴ P73,−209，
∴ tan∠PAB=|yP||xP−xA|=20973+1=23 .
②∵ ∠EAD=∠ACO，且设点P的横坐标为m0∴ tan∠EAD=tan∠ACO=DEAD=OAOC=13，
∴ DE=13AD=131+m.
∵ CF⊥AP，PD⊥x轴，
∴ ∠APD=∠CFO.
又∵ ∠PDA=∠FOC=90∘ ，
∴ △APD∽△CFO，
∴ PDAD=OFOC，
∴ −m2−2m−3m+1=OF3，
∴ OF=9−3m，∴ F9−3m,0．
∵ F9−3m,0，C0,−3，
∴ 直线CF的解析式为y=13−mx−3，
∴ DE=|m3−m−3|=|4m−93−m|，
∴ |4m−93−m|=13m+1，
解得m=2或12或−5±55，
∵ 0∴ m=2或55−5.投中次数
2
3
5
6
7
8
人数
1
2
3
2
1
1
1
2
3
4
1
12
13
14
2
21
23
24
3
31
32
34
4
41
42
43
1
2
3
4
1
12
13
14
2
21
23
24
3
31
32
34
4
41
42
43