



数学八年级下册5.2 菱形教学ppt课件
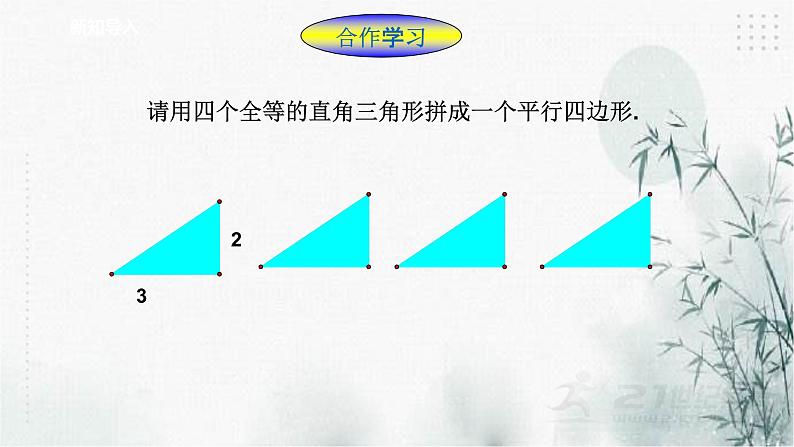
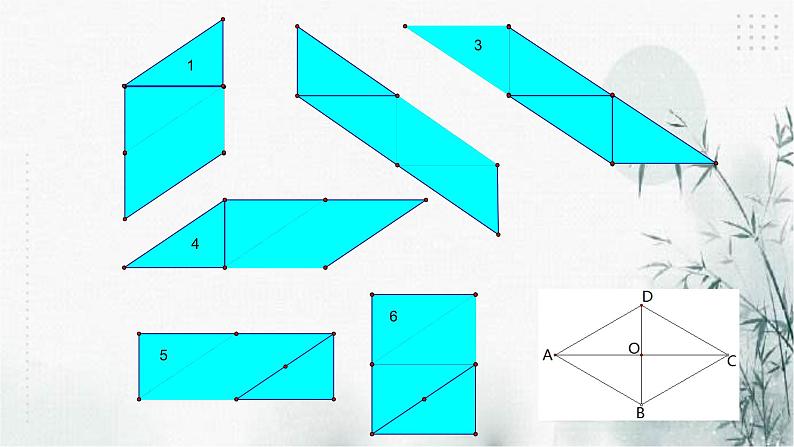
展开请用四个全等的直角三角形拼成一个平行四边形.
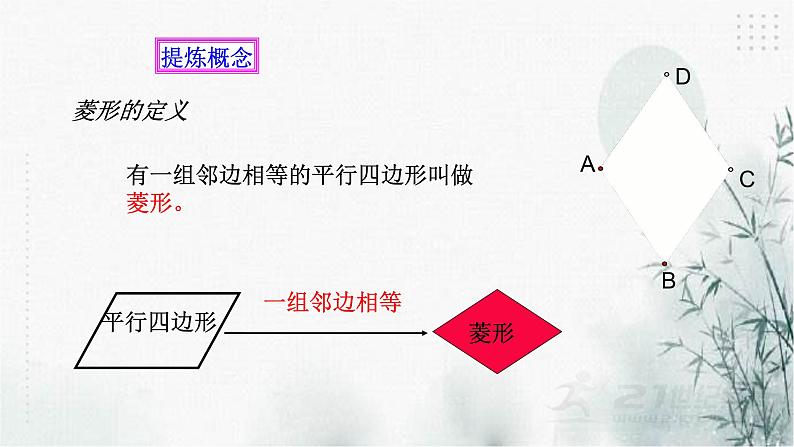
有一组邻边相等的平行四边形叫做菱形。
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
画出菱形的两条对角线,并通过折叠(上下对折、左右对折)手中的图形,得到菱形有哪些平行四边形不具有的性质?从以下方面进行讨论:
1、对称性2、是否有特殊的三角形3、边4、角5、对角线
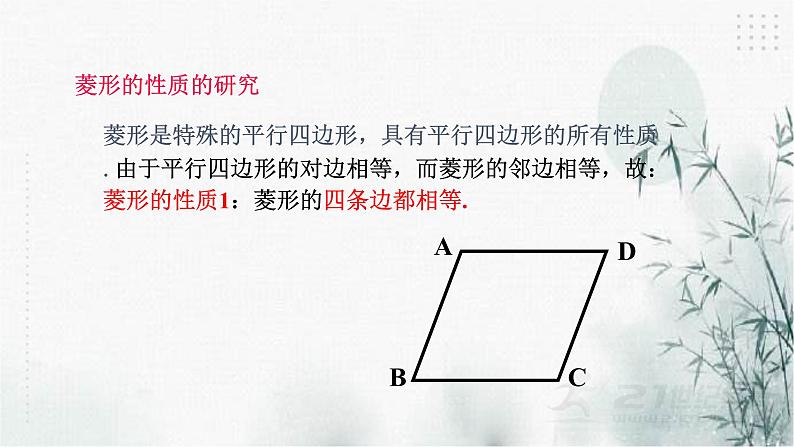
菱形是特殊的平行四边形,具有平行四边形的所有性质.由于平行四边形的对边相等,而菱形的邻边相等,故:菱形的性质1:菱形的四条边都相等.
菱形的两条对角线互相垂直,每一条对角线平分一组对角.
已知:四边形ABCD是菱形.求证: ∠DAC=∠BAC ∠DCA=∠BCA AC⊥BD.
证明:∵四边形ABCD是菱形∴AB=BC=CD=DA又∵ AC = AC∴ △ADC ≌ △ABC∴ ∠DAC=∠BAC ∠DCA=∠BCA
∵四边形ABCD是菱形∴AB=AD,OD=OB又∵ AO = AO∴ △AOD ≌ △AOB∴ ∠DOA=∠BOA又∵ ∠DOA+∠BOA= 180°∴ ∠DOA=∠BOA= 90°∴ AC⊥BD
菱形的性质:1.菱形是特殊的平行四边形,具有一般平行四边形的所有性质.2.特殊的性质:(1) 性质定理1 菱形的四条边都相等.∵四边形ABCD是菱形 , ∴AB=BC=CD=DA.
(2) 性质定理2 菱形的对角线互相垂直,并且每条对角 线平分一组对角.∵四边形ABCD是菱形 , ∴AB⊥CD,AC平分∠DAB和∠DCB.(3) 菱形是轴对称图形,它的对称轴是对角线所在的直线.
例.如图,在菱形ABCD中,对角线AC,BD相交于点O, ∠CAD=30, BD=6,求菱形的边长和对角线AC的长.
解:∵四边形ABCD是菱形,∴AB=CD(菱形的定义)AC平分∠BAD(菱形的每条对角线平分一组对角)∵∠BAC=30°∴∠BAD=60°∴ABD是等边三角形.AB=BD=6又∵OB=OD=3(平行四边形的对角线互相平分)AC⊥BD(菱形的对角线互相垂直)由勾股定理,得AO=AC=2AO=
推广:若菱形的两条对角线长分别为 , ,求菱形的面积。
1.菱形具有而矩形不一定有的性质是 ( )(A) 对角线互相平分 (B) 对角线是内角的平分线(C) 对角线相等 (D) 邻角互补
2.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AB,BC边上的中点,连结EF ,若 EF= , OD=2,则菱形ABCD的面积为________.
3.如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,求AE的长.
解:∵四边形ABCD是菱形,∴AB=BC=CD=AD=5,∴AC⊥BD,AO=1/2AC,BD=2BO,∴∠AOB=90°,∵AC=6,∴AO=3,∴BO=4,∴DB=8,∴菱形ABCD的面积是 1/2×AC•DB=1/2×6×8=24,∴BC•AE=24,AE= .
4.在菱形ABCD中,∠B=60°,点E,F分别在边AB,AD上,且AE=DF.(1)试猜想△ECF的形状,并说明理由;(2)若AB=10,那么△ECF的周长是否存在最小值?如果存在,请求出来;如果不存在,请说明理由.
解:(1)△ECF是等边三角形.理由:连结AC.∵四边形ABCD是菱形,∠B=60°,∴AC=AB=CD,∠CAE=∠D=60°,∠BCD=120°.又∵AE=FD,∴△CEA≌△CFD(SAS),∴CE=CF,∠ACE=∠DCF.又∵∠DCF+∠FCA=1/2∠BCD=60°,∴∠ACE+∠FCA=60°=∠ECF,∴△ECF是等边三角形;
(2)存在.∵△ECF是等边三角形,∴当CE最小时,△ECF的周长最小,∵当CE⊥AB时,CE的长度最小.又∵AB=BC=10,∠B=60°,∠CEB=90°,∴CE= ,∴△ECF的最小周长为 .
每一条对角线平分一组对角
数学八年级下册5.2 菱形授课ppt课件: 这是一份数学八年级下册5.2 菱形授课ppt课件,共22页。PPT课件主要包含了学习目标,探究新知,归纳新知,课堂练习等内容,欢迎下载使用。
数学浙教版5.2 菱形集体备课课件ppt: 这是一份数学浙教版5.2 菱形集体备课课件ppt,共7页。
浙教版5.2 菱形课文ppt课件: 这是一份浙教版5.2 菱形课文ppt课件,共6页。













