2021学年1.3 二次根式的运算课文配套课件ppt

这是一份2021学年1.3 二次根式的运算课文配套课件ppt，共20页。PPT课件主要包含了新知导入，情境引入，124m，试一试，260m，提炼概念，典例精讲，新知讲解，课堂练习，课堂总结等内容，欢迎下载使用。

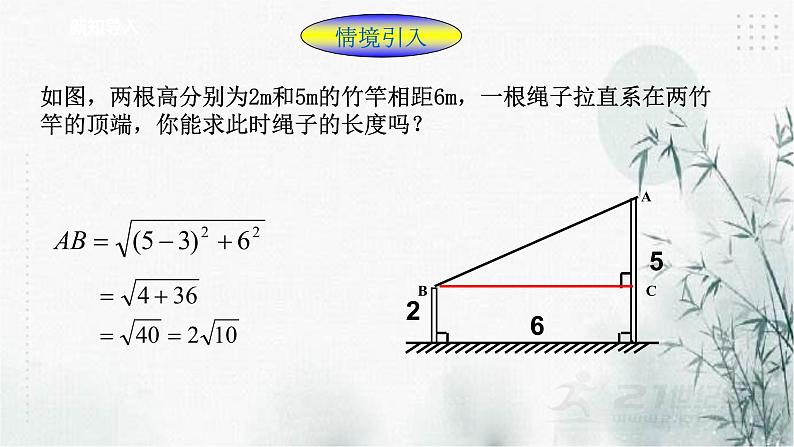
如图，两根高分别为2m和5m的竹竿相距6m，一根绳子拉直系在两竹竿的顶端，你能求此时绳子的长度吗？
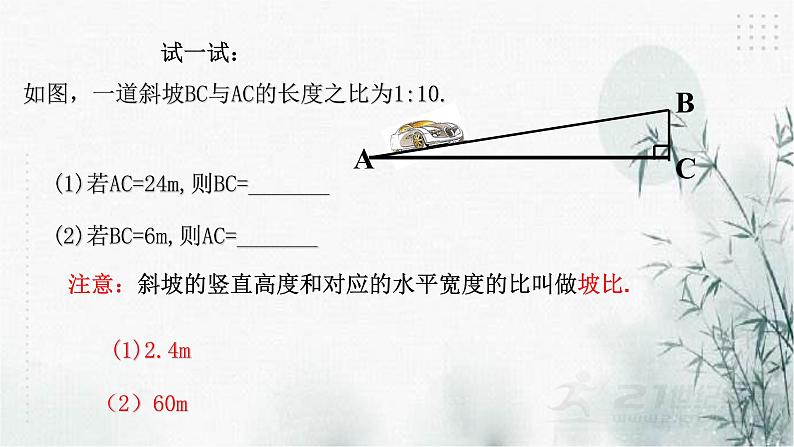
如图，一道斜坡BC与AC的长度之比为1:10.
(1)若AC=24m,则BC=_______
注意：斜坡的竖直高度和对应的水平宽度的比叫做坡比.
(2)若BC=6m,则AC=_______
在日常生活和生产实际中，我们在解决一些问题，尤其是涉及直角三角形的边长计算的问题时，经常用到二次根式及其运算.
二次根式混合运算的结果应写成______________________的形式并且分母中不含二次根式.
最简二次根式（或整式）
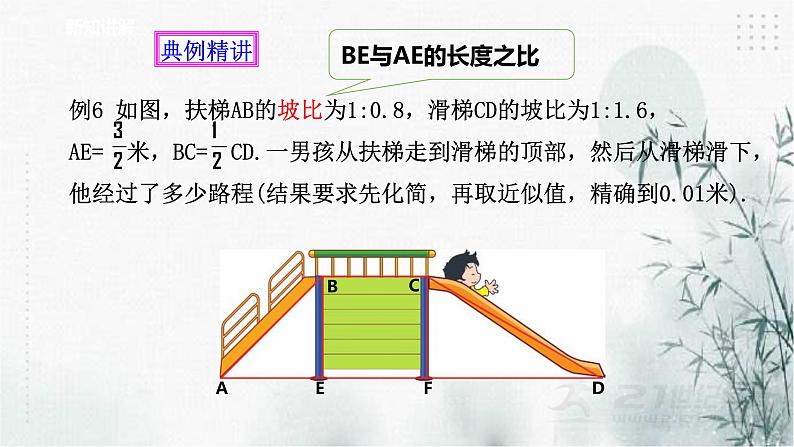
例6 如图，扶梯AB的坡比为1:0.8，滑梯CD的坡比为1:1.6，AE= 米，BC= CD.一男孩从扶梯走到滑梯的顶部，然后从滑梯滑下，他经过了多少路程(结果要求先化简，再取近似值，精确到0.01米).
阅读问题，并结合图形分析问题：（1）所求的路程实际上是哪些线段的和？ 哪些线段的长是已知的？ 哪些线段的长是未知的？ 它们之间有什么关系？（2）列出的算式中有哪些运算？能化简吗？
答：这个男孩经过的总路程约为7.71米.
例7 如图是一张等腰直角三角形彩色纸，AC=BC=40cm，将斜边上的高CD四等分，然后裁出3张宽度相等的长方形纸条.(1)分别求出3张长方形纸条的长度.
解：（1）在Rt△ABC中，AC=BC=40cm,
∵ CD⊥AB，AD=BD ,
同理可得，其余两张长方形纸条的长度依次为：
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠)，如图，正方形美术作品的面积为多少平方厘米cm².
(2)三张长方形纸条连接在一起的总长度为
答：这幅正方形美术作品的面积为200cm2.
1.堤的横断面如图所示．堤高BC是5 m，迎水斜坡AB的长是13 m，那么斜坡AB的坡度是(　 　)
A．1∶3 B．1∶2.6C．1∶2.4 D．1∶2
【解析】 由勾股定理得AC＝12 m.则斜坡AB的坡度＝BC∶AC＝5∶12＝1∶2.4. 选C
(1)求Rt△ABC的面积；(2)求斜边AB的长．
解：(1)∠A＝60°，∠B＝30°；(2)∵∠AOB＝60°＋30°＝90°，∴在Rt△OAB中，设OA＝x，则AB＝2x，
1.用二次根式解决简单的实际问题类型：(1)用二次根式或含二次根式的代数式表示未知量；(2)通过二次根式的四则混合运算求出未知量，并化简．
2.(1)坡度：坡面的垂直高度(h)和水平宽度(l)的比叫做坡度(或坡比)，坡度一般写成1∶m的形式；(2)坡角：坡面与水平面的夹角叫做坡角，记做α；(3)坡度越大，则坡角越大，坡面就越陡，如1∶2>1∶3，则1∶2对应的坡角大，坡面较陡．