苏科版七年级下册12.2 证明习题课件ppt

这是一份苏科版七年级下册12.2 证明习题课件ppt

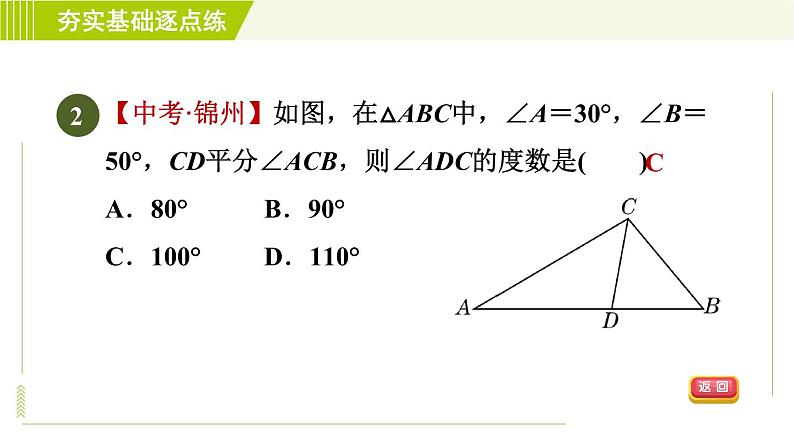
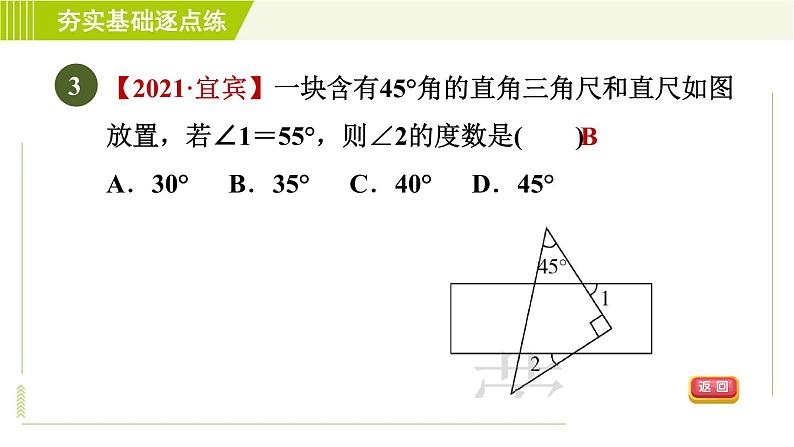
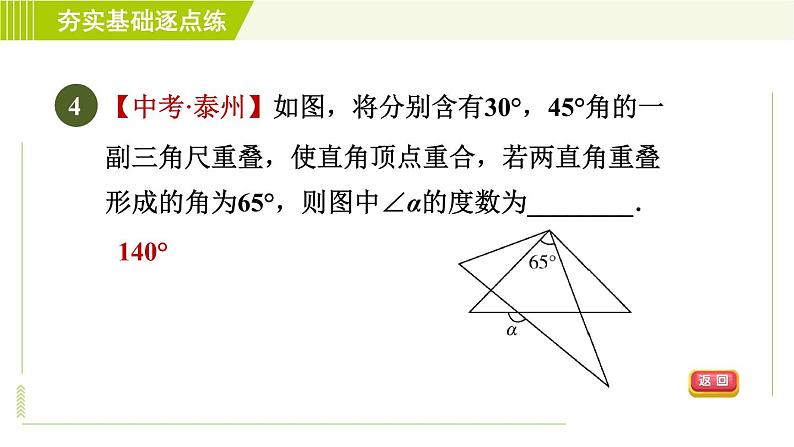
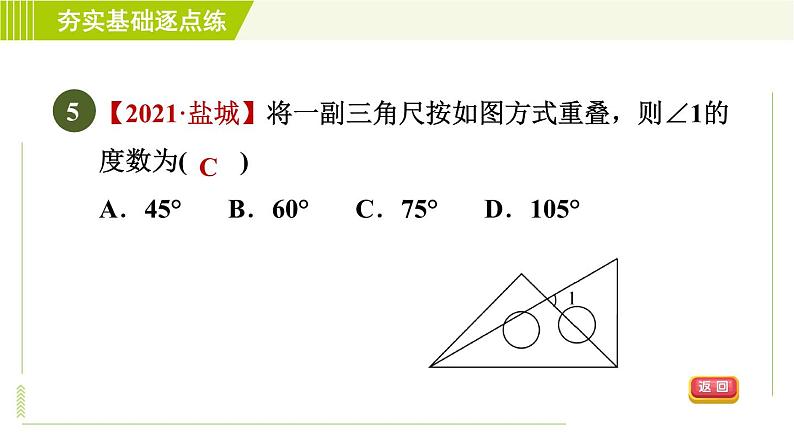
苏科版 七年级下与三角形内角和定理有关的证明12.2.3第12章 证明ACB140°答 案 呈 现习题链接CDCDB习题链接【2021·梧州】在△ABC中，∠A＝20°，∠B＝4∠C，则∠C等于(　　)A．32° B．36° C．40° D．128°A1【中考·锦州】如图，在△ABC中，∠A＝30°，∠B＝50°，CD平分∠ACB，则∠ADC的度数是(　　)A．80° B．90° C．100° D．110°2C【2021·宜宾】一块含有45°角的直角三角尺和直尺如图放置，若∠1＝55°，则∠2的度数是(　　)A．30° B．35° C．40° D．45°3B4【中考·泰州】如图，将分别含有30°，45°角的一副三角尺重叠，使直角顶点重合，若两直角重叠形成的角为65°，则图中∠α的度数为________．140°【2021·盐城】将一副三角尺按如图方式重叠，则∠1的度数为(　　)A．45° B．60° C．75° D．105°5C6如图，∠ACD是△ABC的外角，CE平分∠ACD，若∠A＝60°，∠B＝40°，则∠ECD等于(　　)A．40° B．45° C．50° D．55°C【2021·齐齐哈尔】把直尺与一块三角尺按如图方式放置，若∠1＝47°，则∠2的度数为(　　)A．43° B．47° C．133° D．137°7D【中考·眉山】一副三角尺按如图所示方式摆放，则∠α与∠β的数量关系为(　　)A．∠α＋∠β＝180° B．∠α＋∠β＝225° C．∠α＋∠β＝270° D．∠α＝∠β8B如图，将长方形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F，已知∠BDC＝62°，则∠DFE的度数为(　　)A．31° B．28° C．62° D．56°9D如图，在△ABC中，AD是高，AE，BF是角平分线，它们相交于点O，∠CAB＝50°，∠C＝60°，求∠DAE和∠BOA的度数．解：∵∠CAB＝50°，∠C＝60°，∴∠ABC＝180°－50°－60°＝70°.又∵AD是高，∴∠ADC＝90°，∴∠DAC＝180°－90°－∠C＝30°.∵AE，BF是角平分线，∴∠CBF＝∠ABF＝35°，∠EAF＝25°，∴∠DAE＝∠DAC－∠EAF＝5°，∠AFB＝∠C＋∠CBF＝60°＋35°＝95°，∴∠BOA＝∠EAF＋∠AFB＝25°＋95°＝120°.如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E.(1)若∠B＝35°，∠E＝25°，求∠BAC的度数；解：∵∠B＝35°，∠E＝25°，∴∠ECD＝∠B＋∠E＝60°.∵CE平分∠ACD，∴∠ACE＝∠ECD＝60°，∴∠BAC＝∠ACE＋∠E＝85°.(2)求证：∠BAC＝∠B＋2∠E.证明：∵CE平分∠ACD，∴∠ECD＝∠ACE.∵∠BAC＝∠E＋∠ACE，∴∠BAC＝∠E＋∠ECD.∵∠ECD＝∠B＋∠E，∴∠BAC＝∠E＋∠B＋∠E，∴∠BAC＝2∠E＋∠B.如图，在△ABC中，∠ABC的平分线交AC于点E，过点E作DF∥BC，交AB于点D，且EC平分∠BEF.(1)若∠ADE＝50°，求∠BEC的度数；解：∵DF∥BC，∴∠ADE＝∠ABC＝50°，∠CEF＝∠C.∵BE平分∠ABC，∴∠DBE＝∠EBC＝25°.∵EC平分∠BEF，∴∠CEF＝∠BEC＝∠C.又∵∠BEC＋∠C＋∠EBC＝180°，∴∠BEC＝77.5°.(2)若∠ADE＝α，则∠AED＝________(用含α的代数式表示)．【2021·常熟市期中】已知△ABC中，AD⊥BC于点D，AE平分∠BAC，过点A作直线GH∥BC，且∠GAB＝60°，∠C＝40°，F在BA的延长线上．(1)求∠CAF的度数；解：∵GH∥BC，∠C＝40°，∴∠HAC＝∠C＝40°.∵∠FAH＝∠GAB＝60°，∴∠CAF＝∠HAC＋∠FAH＝100°.(2)求∠DAE的度数．解：∵∠HAC＝40°，∠GAB＝60°，∴∠BAC＝80°.∵AE平分∠BAC，∴∠BAE＝40°.∵GH∥BC，AD⊥BC，∴∠GAD＝90°，∴∠BAD＝90°－60°＝30°，∴∠DAE＝∠BAE－∠BAD＝10°.