高考数学(理数)一轮复习课时作业4《函数及其表示》(原卷版)

课时作业4　函数及其表示

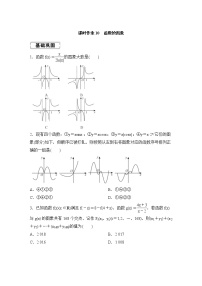
1．下列各组函数中，表示同一函数的是(　　)

A．f(x)＝elnx，g(x)＝x          B．f(x)＝，g(x)＝x－2

C．f(x)＝，g(x)＝sinx       D．f(x)＝|x|，g(x)＝

2．若函数y＝的定义域为R，则实数m的取值范围是(　　)

A.   B.

C.   D.

3．已知f(x5)＝lgx，则f(2)＝(　　)

A.lg2   B.lg5

C.lg2   D.lg3

4．已知函数f(x)＝1－log2x的定义域为[1,4]，则函数y＝f(x)·f(x2)的值域是(　　)

A．[0,1] B．[0,3]

C.   D.

5．若f(x)＝是奇函数，则f(g(－2))的值为(　　)

A.　　　　B．－　　　　C．1　　　　D．－1

6．设函数f(x)＝则满足f(x2－2)＞f(x)的x的取值范围是(　　)

A．(－∞，－1)∪(2，＋∞)

B．(－∞，－)∪(，＋∞)

C．(－∞，－)∪(2，＋∞)

D．(－∞，－1)∪(，＋∞)

7．定义新运算⊕：当a≥b时，a⊕b＝a；当a＜b时，a⊕b＝b2，则函数f(x)＝(1⊕x)x－(2⊕x)，x∈[－2,2]的最大值等于(　　)

A．－1 B．1 

C．6 D．12

8．设函数f(x)＝若f(1)是f(x)的最小值，则实数a的取值范围为(　　)

A．[－1,2) B．[－1,0]

C．[1,2] D．[1，＋∞)

9．函数f(x)＝＋ln(x＋4)的定义域为      _．

10．设函数f(x)＝则使f(x)＝的x的集合为         .

11．记函数f(x)＝的定义域为A，g(x)＝lg[(x－a－1)(2a－x)](a＜1)的定义域为B.若B⊆A，则实数a的取值范围为                 .

12．已知函数f(x)对任意实数x均有f(x)＝－2f(x＋1)，且f(x)在区间[0,1]上有解析式f(x)＝x2.

(1)求f(－1)，f(1.5)；

(2)写出f(x)在区间[－2,2]上的解析式．

13．如图，修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切)．已知环湖弯曲路段为某三次函数图象的一部分，则该函数的解析式为(　　)

A．y＝x3－x2－x B．y＝x3＋x2－3x

C．y＝x3－x D．y＝x3＋x2－2x

14．设函数f(x)＝若f(x)的最大值不超过1，则实数a的取值范围为(　　)

A.   B.

C.   D.