初中数学冀教版八年级下册第二十一章 一次函数综合与测试习题

八年级数学下册第二十一章一次函数专项练习

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、关于一次函数，下列结论不正确的是（       ）

A．图象与直线平行

B．图象与轴的交点坐标是

C．随自变量的增大而减小

D．图象经过第二、三、四象限

2、已知点（﹣1，y1），（4，y2）在一次函数y＝3x+a的图象上，则y1，y2的大小关系是（　　）

A．y1＜y2 B．y1＝y2 C．y1＞y2 D．不能确定

3、如图，一次函数y＝kx＋b（k＞0）的图像过点，则不等式的解集是（     ）

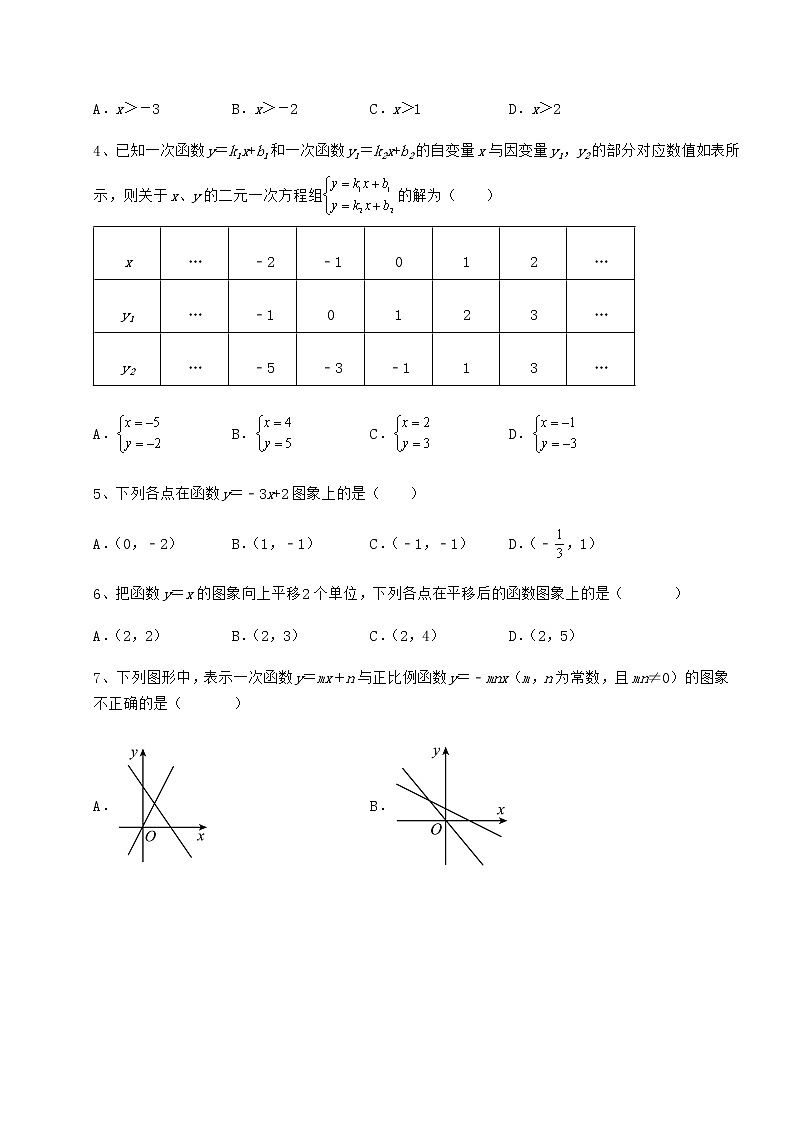
A．x＞－3 B．x＞－2 C．x＞1 D．x＞2

4、已知一次函数y＝k1x+b1和一次函数y1＝k2x+b2的自变量x与因变量y1，y2的部分对应数值如表所示，则关于x、y的二元一次方程组的解为（　　）

A． B． C． D．

5、下列各点在函数y＝﹣3x+2图象上的是（　　）

A．（0，﹣2） B．（1，﹣1） C．（﹣1，﹣1） D．（﹣，1）

6、把函数y＝x的图象向上平移2个单位，下列各点在平移后的函数图象上的是（       ）

A．（2，2） B．（2，3） C．（2，4） D．（2，5）

7、下列图形中，表示一次函数y＝mx＋n与正比例函数y＝﹣mnx（m，n为常数，且mn≠0）的图象不正确的是（       ）

A．  B．

C． D．

8、甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（千米）与甲车行驶的时间t（小时）之间的函数关系如图所示．

则下列结论：

①A，B两城相距300千米；                        

②乙车比甲车晚出发1小时，却早到1小时；

③乙车出发后2.5小时追上甲车；

④当甲、乙两车相距50千米时，或．

其中正确的结论有（       ）

A．1个 B．2个 C．3个 D．4个

9、巴中某快递公司每天上午7：00﹣8：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，下列说法正确的个数为（　　）

①15分钟后，甲仓库内快件数量为180件；

②乙仓库每分钟派送快件数量为8件；

③8：00时，甲仓库内快件数为400件；

④7：20时，两仓库快递件数相同．

A．1个 B．2个 C．3个 D．4个

10、已知正比例函数的图像经过点（2，4）、（1，）、（1，），那么与的大小关系是（        ）

A．  B．  C．  D．无法确定

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、一条笔直的公路上顺次有A，B，C三地，甲车从B地出发匀速向C地行驶，同时乙车从B地出发匀速向A地行驶，到达A地并在A地停留1小时后，调头将速度提高了50% 向C地行驶，两车到达C地均停止运动.在两车行驶的过程中，甲乙两车之间的距离s(千米)与行驶时间t (小时)之间的函数图象如图所示，当甲乙两车第一次相遇时，距A地的距离为_________ 千米．

2、如图1是甲、乙两个圆柱形容器的轴截面示意图，乙容器中有一个圆柱形铁块立放其中（圆柱形铁块的下底面完全落在乙容器底面上），现将甲容器中的水匀速注入乙容器，甲、乙两个容器中水的深度与注水时间（分钟）之间的关系如图2所示，若乙容器中铁块的体积是，则甲容器的底面积是______．

3、求一元一次方程kx＋b＝0的解

从函数值看：求y＝_____时一次函数y＝ kx＋b中x的值

从函数图象看：求直线y＝ kx＋b与_____交点的横坐标

4、已知正比例函数y＝kx（k≠0）的函数值y随x增大而减小，则直线：y＝﹣kx＋k不经过第____象限．

5、一般地，形如y＝kx＋b（k≠0，k、b为常数）的函数，叫做______函数．注意：k是常数，k≠0，k可以是正数、也可以是负数；b可以取______ ．

三、解答题（5小题，每小题10分，共计50分）

1、已知y与x﹣2成正比例，且当x＝1时，y＝﹣2

(1)求变量y与x的函数关系式；

(2)请在给出的平面直角坐标系中画出此函数的图象；

(3)已知点A在函数y＝ax＋b的图象上，请直接写出关于x的不等式ax＋b＞2x﹣4的解集　    　．

2、某厂计划生产A，B两种产品若干件，已知两种产品的成本价和销售价如下表：

(1)第一次工厂用220000元资金生产了A，B两种产品共600件，求两种产品各生产多少件？

(2)第二次工厂生产时，工厂规定A种产品生产数量不得超过B种产品生产数量的一半．工厂计划生产两种产品共3000件，应如何设计生产方案才能获得最大利润，最大利润是多少？

3、直线，与直线相交于点．

(1)求直线的解析式；

(2)横、纵坐标都是整数的点叫做整点．记直线与直线和轴围成的区域内（不含边界）为．

①当时，直接写出区域内的整点个数；

②若区域内的整点恰好为2个，结合函数图象，求的取值范围．

4、－辆货车从甲地到乙地，一辆轿车从乙地到甲地，两车沿同一条公路分别从甲、乙两地同时出发，匀速行驶．已知轿车比货车每小时多行驶20km；两车相遇后休息了24分钟，再同时继续行驶，设两车之间的距离为y（km），货车行驶时间为x（h），请结合图像信息解答下列问题：

(1)货车的速度为______km/h，轿车的速度为______km/h；

(2)求y与x之间的函数关系式（写出x的取值范围），并把函数图像画完整；

(3)货车出发______h，与轿车相距30km．

5、已知一次函数，完成下列问题：

(1)求此函数图像与x轴、y轴的交点坐标；

(2)画出此函数的图像：观察图像，当时，x的取值范围是______．

-参考答案-

一、单选题

1、D

【解析】

【分析】

根据一次函数的性质对A、C、D进行判断；根据一次函数图象上点的坐标特征对D进行判断，，随的增大而增大，函数从左到右上升；，随的增大而减小，函数从左到右下降．由于与轴交于，当时，在轴的正半轴上，直线与轴交于正半轴；当时，在轴的负半轴，直线与轴交于负半轴．

【详解】

解：A、函数的图象与直线平行，故本选项说法正确；

B、把代入，所以它的图象与轴的交点坐标是，故本选项说法正确；

C、，所以随自变量的增大而减小，故本选项说法正确；

D、，，函数图象经过第一、二、四象限，故本选项说法不正确；

故选：D．

【点睛】

本题考查了一次函数的性质，以及k对自变量和因变量间的关系的影响，熟练掌握k的取值对函数的影响是解决本题的关键．

2、A

【解析】

【分析】

根据一次函数y＝3x+a的一次项系数k＞0时，函数值随自变量的增大而增大的性质来求解即可．

【详解】

解：∵一次函数y＝3x+a的一次项系数为3＞0，

∴y随x的增大而增大，

∵点（﹣1，y1），（4，y2）在一次函数y＝3x+a的图象上，﹣1＜4，

∴y1＜y2，

故选：A．

【点睛】

本题考查了一次函数的性质，掌握，时，随的增大而增大是解题的关键．

3、C

【解析】

【分析】

先将（－1，0）代入y＝kx＋b中得到k=b，则不等式化为，根据k＞0解关于x的不等式即可．

【详解】

解：将（－1，0）代入y＝kx＋b中得：－k+b=0，解得：k=b，

则不等式化为，

∵k＞0，

∴（x－2）+1＞0，

解得：x＞1，

故选：C．

【点睛】

本题考查了一次函数与一元一次不等式的关系，根据一次函数图象上的点的坐标特征求得k与b的关系是解答的关键．

4、C

【解析】

【分析】

利用方程组的解就是两个相应的一次函数图象的交点坐标解决问题．

【详解】

解：由表格可知，一次函数y1=k1x+b1和一次函数y2=k2x+b2的图象都经过点(2，3)，

∴一次函数y1=k1x与y=k2x+b的图象的交点坐标为(2，3)，

∴关于x，y的二元一次方程组的解为．

故选：C．

【点睛】

本题考查了一次函数图像交点坐标与方程组解的关系：对于函数y1=k1x+b1，y2=k2x+b2，其图象的交点坐标(x，y)中x，y的值是方程组的解．

5、B

【解析】

【分析】

根据一次函数图象上点的坐标满足函数解析式，逐一判断，即可得到答案．

【详解】

∵，

∴A不符合题意，

∵，

∴B符合题意，

∵，

∴C不符合题意，

∵，

∴D不符合题意，

故选B．

【点睛】

本题主要考查一次函数图象上点的坐标，掌握一次函数图象上点的坐标满足函数解析式，是解题的关键．

6、C

【解析】

【分析】

由函数“上加下减”的原则解题．

【详解】

解：由“上加下减”的原则可知，将直线y＝x的图象向上平移2个单位所得直线的解析式为：y＝x+2，

当x＝2时，y＝2+2＝4，

所以在平移后的函数图象上的是（2，4），

故选：C．

【点睛】

本题考查函数图象的平移，一次函数图象的性质等知识，是基础考点，掌握相关知识是解题关键．

7、B

【解析】

【分析】

利用一次函数的性质逐项进行判断即可解答．

【详解】

解：A、由一次函数的图象可知，，故；由正比例函数的图象可知，两结论一致，故本选项不符合题意；

B、由一次函数的图象可知，，故；由正比例函数的图象可知，两结论不一致，故本选项符合题意；

C. 由一次函数的图象可知，，故；由正比例函数的图象可知，两结论一致，故本选项不符合题意；

D. 由一次函数的图象可知，，故；由正比例函数的图象可知，两结论一致，故本选项不符合题意；

故选B．

【点睛】

本题考查了一次函数的图象性质，要掌握它的性质才能灵活解题．一次函数的图象有四种情况：当，函数的图象经过第一、二、三象限；当，函数的图象经过第一、三、四象限；当，函数的图象经过第一、二、四象限；当，函数的图象经过第二、三、四象限．

8、B

【解析】

【分析】

当不动时，距离300千米，就是A，B两地的距离；甲匀速运动，走完全程用时5小时，乙走完全程用时3小时，确定甲，乙的函数解析式，求交点坐标；分甲出发，乙未动，距离为50千米，甲出发，乙出发，且甲在前50距离50千米，甲在后距离50千米，乙到大时距离为50千米四种情形计算即可．

【详解】

∵（0，300）表示不动时，距离300千米，就是A，B两地的距离，

∴①正确；

∵甲匀速运动，走完全程用时5小时，乙走完全程用时3小时，

∴乙车比甲车晚出发1小时，却早到1小时；

∴②正确；

设，

∴300=5m，

解得m=60，

∴；

设，

∴

解得，

∴；

∴

解得t=2.5，

∴2.5-1=1.5，

∴乙车出发后1.5小时追上甲车；

∴③错误；

当乙未出发时，，

解得t=；

当乙出发，且在甲后面时，，

解得t=；

当乙出发，且在甲前面时，，

解得t=；

当乙到大目的地，甲自己行走时，，

解得t=；

∴④错误；

故选B．

【点睛】

本题考查了函数的图像，一次函数的解析式确定，交点的意义，熟练掌握待定系数法，准确捕获图像信息是解题的关键．

9、B

【解析】

【分析】

根据图象可知15分钟后，甲仓库内快件数量为130件，据此可得甲仓库揽收快件的速度，进而得出时，甲仓库内快件数；由图象可知45分钟，乙仓库派送快件数量为180件，可得乙仓库每分钟派送快件的数量，进而得出乙仓库快件的总数量，然后根据题意列方程即可求出两仓库快递件数相同是时间．

【详解】

解：由题意结合图象可知：

15分钟后，甲仓库内快件数量为130件，故①说法错误；

甲仓库揽收快件的速度为：（件分），

所以时，甲仓库内快件数为：（件，故③说法正确；

（分，

即45分钟乙仓库派送快件数量为180件，

所以乙仓库每分钟派送快件的数量为：（件，故②说法错误；

所以乙仓库快件的总数量为：（件，

设分钟后，两仓库快递件数相同，根据题意得：

，

解得，

即时，两仓库快递件数相同，故④说法正确．

所以说法正确的有③④共2个．

故选：B．

【点睛】

本题考查了一次函数的应用，解题的关键是结合图象，理解图象中点的坐标代表的意义．

10、A

【解析】

【分析】

先求出正比例函数解析式根据正比例函数的图象性质，当k＜0时，函数随x的增大而减小，可得y1与y2的大小．

【详解】

解：∵正比例函数的图像经过点（2，4）、代入解析式得

解得

∴正比例函数为

∵＜0，

∴y随x的增大而减小，

由于-1＜1，故y1<y2．

故选：A．

【点睛】

本题考查了正比例函数图象上点的坐标特征，用到的知识点为：正比例函数的图象，当k＜0时，y随x的增大而减小是解题关键．

二、填空题

1、432

【解析】

【分析】

设甲的速度为v甲，乙的速度为v乙，根据题意可得v甲+v乙=100①，可求出乙追上甲的时间为4.8h，根据题意可得4.8×（1+50%）V乙=2V乙+7.8V甲②，联立①②求出两车的速度即可解答．

【详解】

解：如图：

设甲的速度为v甲，乙的速度为v乙，

OD段：两人的速度和为：200÷2=100（km/h），

即v甲+v乙=100①，

此时乙休息1h，则E处的横坐标为：2+1=3，

则乙用了：7.8-3=4.8（h）追上甲，

则4.8×（1+50%）V乙=2V乙+7.8V甲②，

联立①②得V甲=40，V乙=60，

则第一次相遇是在7.8h时，

距离A地：4.8×（1+50%）×60=432（km）．

故答案为：432．

【点睛】

本题主要考查了一次函数的应用．理解函数图象的点的坐标的实际意义，从而得到甲乙两车的行驶的距离和速度是解题的关键．

2、80

【解析】

【分析】

设甲容器的底面积为，乙容器的底面积为，根据拐点（3，17），得到铁块的高度为17cm，从而得到铁块的底面积为=12（），确定= -3x+15，当x=3时，=6，从而得到6=（25-17），从而得到9=（17-2）（-12），求解即可．

【详解】

设甲容器的底面积为，乙容器的底面积为，

∵拐点（3，17），

∴铁块的高度为17cm，

∴铁块的底面积为=12（），

设=kx+15，

把（5，0）代入，得5k+15=0，

解得k=-3，

∴= -3x+15，

当x=3时，

=6，

∴6=（25-17），

即=，

∵9=（17-2）（-12），

∴=80（），

故答案为：80．

【点睛】

本题考查了一次函数的解析式，圆柱的体积，熟练掌握一次函数解析式的确定，正确读懂函数信息是解题的关键．

3、     0     x轴

【解析】

略

4、二

【解析】

【分析】

根据正比例函数的图象和性质得出的取值范围，再根据的取值和一次函数的增减性进行判断即可．

【详解】

解：正比例函数的函数值随增大而减小，

，

，

即直线：中的，，

因此直线经过一、三、四象限，不过第二象限，

故答案为：二．

【点睛】

本题考查一次函数的图象和性质，解题的关键是掌握一次函数的图象和性质是正确判断的前提，理解一次函数中、的符号决定一次函数的性质也是正确判断的关键．

5、     一次     任意实数

【解析】

略

三、解答题

1、 (1)y＝2x﹣4

(2)见解析

(3)x＜3

【解析】

【分析】

（1）设y＝k（x﹣2）（k为常数，k≠0），把x＝1，y＝﹣2代入得：﹣2＝k（1﹣2），求出k＝2即可；

（2）列表描点连线即可；

（3）先确定A点的坐标是（3，2），把A点的横坐标代入y＝2x﹣4求出函数值=2，即点A也在函数y＝2x﹣4的图象上，点A是函数y＝ax+b和函数y＝2x﹣4的交点，然后利用图像法求不等式的解集即可．

(1)

解：∵y与x﹣2成正比例，

∴设y＝k（x﹣2）（k为常数，k≠0），

把x＝1，y＝﹣2代入得：﹣2＝k（1﹣2），

解得：k＝2，

即y＝k（x﹣2）＝2（x﹣2）＝2x﹣4，

所以变量y与x的函数关系式是y＝2x﹣4；

(2)

列表

描点（0，-4），（2，0），

连线得y＝2x﹣4的图象；

(3)

从图象可知：A点的坐标是（3，2），把A点的横坐标x=3代入y＝2x﹣4时，y=2，

即点A也在函数y＝2x﹣4的图象上，

即点A是函数y＝ax+b和函数y＝2x﹣4的交点，

∴关于x的不等式ax+b＞2x﹣4反应在函数图像函数y＝ax+b在函数y＝2x﹣4图像上方，交点A的左侧，

所以关于x的不等式ax+b＞2x﹣4的解集是x＜3，

故答案为：x＜3．

【点睛】

本题考查待定系数法求函数解析式，描点法画函数图像，用图像法求不等式的解集，掌握待定系数法求函数解析式，描点法画函数图像，用图像法求不等式的解集是解题关键．

2、 (1)A种产品生产400件，B种产品生产200件

(2)A种产品生产1000件时，利润最大为460000元

【解析】

【分析】

（1）设A种产品生产x件，则B种产品生产（600-x）件，根据600件产品用220000元资金，即可列方程求解；

（2）设A种产品生产x件，总利润为w元，得出利润w与A产品数量x的函数关系式，根据增减性可得，A产品生产越多，获利越大，因而x取最大值时，获利最大，据此即可求解．

(1)

解：设A种产品生产x件，则B种产品生产（600-x）件，

由题意得：，

解得：x＝400，

600-x=200，

答：A种产品生产400件，B种产品生产200件.

(2)

解：设A种产品生产x件，总利润为w元，由题意得：

由，

得：，

因为10>0，w随x的增大而增大 ，所以当x＝1000时，w最大＝460000元．

【点睛】

本题考查一元一次方程、一元一次不等式以及一次函数的实际应用. 解答本题的关键是明确题意，利用一次函数的性质和不等式的性质解答．

3、 (1)直线为；

(2)①当时，整点个数为1个，为；②的取值范围为或

【解析】

【分析】

（1）根据待定系数法求得即可；

（2）①当k＝1时代入点A坐标即可求出直线解析式，进而分析出整点个数；

②当k＜0时分别以（1，2），（2，1）；（1，2），（3，1）为边界点代入确定k的值；当k>0时分别以（1，2），（−1，1）；（1，2），（−2，1）为边界点代入确定k的值，根据图形即可求得k的取值范围．

(1)

解：直线过点．

，

直线为．

(2)

解：①当时，，把代入得，

解得：，

，

如图1，

区域内的整点个数为1个，为．

②如图2，若，

当直线过，时，．

当直线过，时，．

，

如图3，若，

当直线过，时，．

当直线过，时，．

．

综上，若区域内的整点恰好为2个，的取值范围为或．

【点睛】

此题主要考查待定系数法求一次函数的解析式，会运用边界点分析问题是解题的关键．

4、 (1)80，100

(2)当时，；当时，；当时，；当时，，图见解析

(3)或

【解析】

【分析】

（1）结合图象可得经过两个小时，两车相遇，设货车的速度为，则轿车的速度为，根据题意列出方程求解即可得；

（2）分别求出各个时间段的函数解析式，然后再函数图象中作出相应直线即可；

（3）将代入（2）中各个时间段的函数解析式，求解，同时考虑解是否在相应时间段内即可．

(1)

解：由图象可得：经过两个小时，两车相遇，

设货车的速度为，则轿车的速度为，

∴，

解得：，，

∴货车的速度为，则轿车的速度为，

故答案为：80；100；

(2)

当时，图象经过，点，

设直线解析式为：，代入得：

，

解得：，

∴当时，；

分钟小时，

∵两车相遇后休息了24分钟，

∴当时，；

当时，轿车距离甲地的路程为：，货车距离乙地的路程为：，

轿车到达甲地还需要：，

货车到达乙地还需要：，

∴当时，；

当时，；

当时，；

当时，；

当时，；

∴函数图象分别经过点，，，

作图如下：

(3)

①当时，令可得：

，

解得：；

②当时，令可得：

，

解得：；

③当时，令可得：

；

解得：：，不符合题意，舍去；

综上可得：货车出发或，与轿车相距30km，

故答案为：或．

【点睛】

题目主要考查一元一次方程的应用，一次函数的应用，利用待定系数法确定一次函数解析式，作函数图象等，理解题意，熟练掌握运用一次函数的基本性质是解题关键．

5、 (1)；

(2)作图见解析；

【解析】

【分析】

（1）分别令，进而即可求得此函数图象与坐标轴的交点坐标；

（2）根据（1）所求得的点的坐标，画出一次函数图象即可，根据图象写出当时，自变量的取值范围即可．

(1)

令，解得，令，解得

则此函数图像与x轴的交点坐标为、与y轴的交点坐标为

(2)

过点；作直线，如图，

根据函数图象可得当时，x的取值范围是:

故答案为：

【点睛】

本题考查了画一次函数图象，一次函数与坐标轴的交点，根据函数图象求自变量的范围，掌握一次函数的图象的性质是解题的关键．