初中数学冀教版八年级下册第二十一章 一次函数综合与测试课后练习题

这是一份初中数学冀教版八年级下册第二十一章 一次函数综合与测试课后练习题，共30页。
八年级数学下册第二十一章一次函数综合测评
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、已知点，在一次函数y＝－2x－b的图像上，则m与n的大小关系是（ ）
A．m＞n B．m＝n C．m＜n D．无法确定
2、如图，在Rt△ABO中，∠OBA＝90°，A（4，4），且，点D为OB的中点，点P为边OA上的动点，使四边形PDBC周长最小的点P的坐标为（ ）

A．（2，2） B．（，） C．（，） D．（，）
3、已知点和点是一次函数图象上的两点，若，则下列关于的值说法正确的是（ ）
A．一定为正数 B．一定为负数 C．一定为0 D．以上都有可能
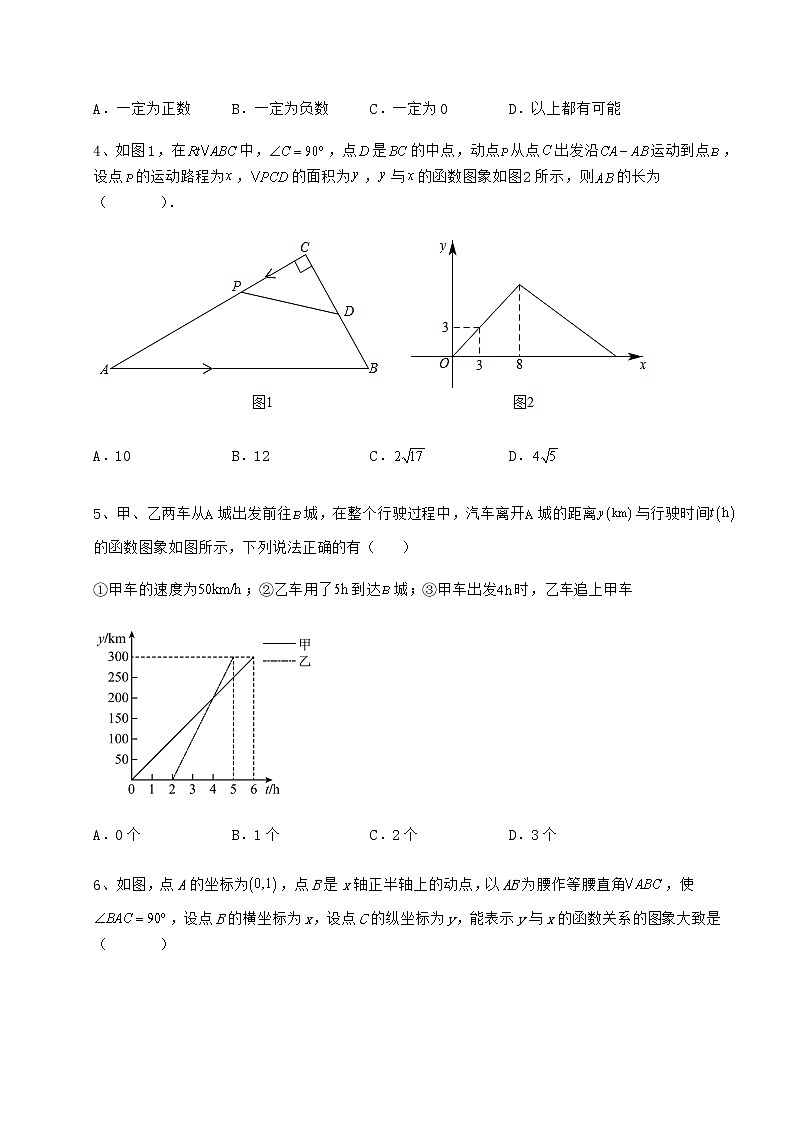
4、如图1，在中，，点是的中点，动点从点出发沿运动到点，设点的运动路程为，的面积为，与的函数图象如图2所示，则的长为（ ）．

A．10 B．12 C． D．
5、甲、乙两车从城出发前往城，在整个行驶过程中，汽车离开城的距离与行驶时间的函数图象如图所示，下列说法正确的有（　　）
①甲车的速度为；②乙车用了到达城；③甲车出发时，乙车追上甲车

A．0个 B．1个 C．2个 D．3个
6、如图，点A的坐标为，点B是x轴正半轴上的动点，以AB为腰作等腰直角，使，设点B的横坐标为x，设点C的纵坐标为y，能表示y与x的函数关系的图象大致是（ ）

A． B．
C． D．
7、一次函数y1＝kx+b与y2＝mx+n的部分自变量和对应函数值如表：
x
…
﹣2
﹣1
0
1
2
…
y1
…
1
2
3
4
5
…

x
…
﹣2
﹣1
0
1
2
…
y2
…
5
2
﹣1
﹣4
﹣7
…
则关于x的不等式kx+b＞mx+n的解集是（　　）
A．x＞0 B．x＜0 C．x＜﹣1 D．x＞﹣1
8、一次函数，，且随的增大而减小，则其图象可能是（ ）
A． B．
C． D．
9、已知一次函数y=mnx与y=mx+n(m，n为常数，且mn≠0)，则它们在同一平面直角坐标系内的图象可能为（ ）
A． B．
C． D．
10、我边防局接到情报，近海处有一可疑船只A正向公海方向行驶，边防局迅速派出快艇B追赶（图1）．图2中，分别表示两船相对于海岸的距离s（海里）与追赶时间t（分）之间的关系，下列说法错误的是（ ）．

A．快艇的速度比可疑船只的速度快0.3海里/分
B．5分钟时快艇和可疑船只的距离为3.5海里
C．若可疑船只一直匀速行驶，则它从海岸出发0.5小时后，快艇才出发追赶
D．当快艇出发分钟后追上可疑船只，此时离海岸海里
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、某工厂有甲、乙、丙、丁四个不同的车间生产电子元件，由于生产设备不同，工人在不同车间日生产量也不一定相同，但皆为整数．某日，该工厂接到一批生产订单，工厂老板想将工人合理分配到不同车间，已知甲车间的工人数与乙车间相同，丙车间的工人数是丁车间的倍且比甲车间工人数多，甲车间与丁车间的工人数之和不少于人且不超过人；甲车间与丁车间每个工人的日生产量相同，乙车间每个工人的日生产量为丙车间每个工人日生产量的倍，甲车间与丙车间每个工人的日生产量之和为件，且甲车间每个工人的日生产量不低于丙车间每个工人日生产量的且不超过件；甲车间、丙车间的日生产之和比乙车间、丁车间的日生产之和少件．则当甲、丙两车间当日生产量之和最多时，该工厂调配前往甲车间的人数为__________人．
2、甲、乙两车分别从，两地同时相向匀速行驶，当乙车到达地后，继续保持原速向远离的方向行驶，而甲车到达地后立即掉头，并保持原速与乙车同向行驶，经过12小时后两车同时到达距地300千米的地（中途休息时间忽略不计）．设两车行驶的时间为（小时），两车之间的距离为（千米），与之间的函数关系如图所示，则当甲车到达地时，乙车距地 __千米．

3、如果点P1(3，y1)，P2(2，y2)在一次函数y=8x-1的图像上，那么y1______y2．(填“＞”、“＜”或“=”)
4、已知一次函数的图象（如图），则不等式 ＜0的解集是___________

5、如图，正比例函数 y＝kx（k≠0）的图像经过点 A（2，4），AB⊥x 轴于点 B，将△ABO 绕点 A逆时针旋转 90°得到△ADC，则直线 AC 的函数表达式为_____．

三、解答题（5小题，每小题10分，共计50分）
1、已知一次函数y＝kx﹣4，当x＝3时，y＝﹣1，求它的解析式以及该直线与坐标轴的交点坐标．
2、已知 A、B 两地相距 3km，甲骑车匀速从 A 地前往 B 地，如图表示甲骑车过程中离 A 地的路程 y 甲（km）与他行驶所用的时间 x（min）之间的关系．根据图像解答下列问题：

(1)甲骑车的速度是 km/min；
(2)若在甲出发时，乙在甲前方 1.2km 的 C 处，两人均沿同一路线同时匀速出发前往 B 地，在第 4 分钟甲追上了乙，两人到达 B 地后停止．请在下面同一平面直角坐标系中画出乙离 B 地的距离 y 乙（km）与所用时间 x（min）的关系的大致图像；
(3)在（2）的条件下，求出两个函数图像的交点坐标，并解释它的实际意义．
3、已知一次函数的图象与轴交于点，与轴交于点
(1)求、两点的坐标；
(2)画出函数的图象
4、为了贯彻落实市委市政府提出的“精准扶贫”精神．某校特制定了一系列关于帮扶A，B两贫困村的计划．现决定从某地运送168箱小鸡到A，B两村养殖，若用大、小货车共18辆，则恰好能一次性运完这批小鸡，已知这两种大、小货车的载货能力分别为10箱/辆和8箱/辆，其运往A、B两村的运费如下表：
目的地车型
A村（元/辆）
B村（元/辆）
大货车
80
90
小货车
40
60
(1)试求这18辆车中大、小货车各多少辆？
(2)现安排其中10辆货车前往A村，其余货车前往B村，设前往4村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数表达式，并直接写出自变量取值范围；
(3)在（2）的条件下，若运往A村的小鸡不少于96箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
5、如图，直线l：与y轴交于点G，直线l上有一动点P，过点P作y轴的平行线PE，过点G作x轴的平行线GE，它们相交于点E．将△PGE沿直线l翻折得到△PGE′，点E的对应点为E′．

(1)如图1，请利用无刻度的直尺和圆规在图1中作出点E的对应点E′；
(2)如图2，当点E的对应点E′落在x轴上时，求点P的坐标；
(3)如图3，直线l上有A，B两点，坐标分别为(－2，－6)，(4，6)，当点P从点A运动到点B的过程中，点E′也随之运动，请直接写出点E′的运动路径长为____________．

-参考答案-
一、单选题
1、A
【解析】
【分析】
由k＝−2＜0，利用一次函数的性质可得出y随x的增大而减小，结合＜可得出m＞n．
【详解】
解：∵k＝−2＜0，
∴y随x的增大而减小，
又∵点A（，m），B（，n）在一次函数y＝−2x＋1的图象上，且＜，
∴m＞n．
故选：A．
【点睛】
本题考查了一次函数的性质，牢记“k＞0，y随x的增大而增大；k＜0，y随x的增大而减小”是解题的关键．
2、C
【解析】
【分析】
先确定点D关于直线AO的对称点E（0，2），确定直线CE的解析式，直线AO的解析式，两个解析式的交点就是所求．
【详解】
∵∠OBA＝90°，A（4，4），且，点D为OB的中点，
∴点D（2，0），AC=1，BC=3，点C（4，3），
设直线AO的解析式为y=kx，
∴4=4k,
解得k=1，
∴直线AO的解析式为y=x，
过点D作DE⊥AO，交y轴于点E，交AO于点F，
∵∠OBA＝90°，A（4，4），
∴∠AOE=∠AOB=45°，
∴∠OED=∠ODE=45°，OE=OD，
∴DF=FE，
∴点E是点D关于直线AO的对称点，
∴点E（0，2），
连接CE，交AO于点P，此时，点P是四边形PCBD周长最小的位置，
设CE的解析式为y=mx+n，

∴，
解得，
∴直线CE的解析式为y=x+2，
∴y=14x+2y=x，
解得，
∴使四边形PDBC周长最小的点P的坐标为（，），
故选C．
【点睛】
本题考查了一次函数的解析式，将军饮马河原理，熟练掌握待定系数法和将军饮马河原理是解题的关键．
3、A
【解析】
【分析】
由 可得一次函数的性质为随的增大而增大，从而可得答案.
【详解】
解：点和点是一次函数图象上的两点，，
随的增大而增大，
即一定为正数，
故选A
【点睛】
本题考查的是一次函数的增减性的应用，掌握“一次函数，随的增大而增大， 则”是解本题的关键.
4、D
【解析】
【分析】
由图像可知， 当时，y与x的函关系为：y=x，当x=8时，y=8，即P与A重合时，的面积为8，据此求出CD，BC，再根据勾股定理求出AB即可P．
【详解】
解：如图2，当时，设y=kx，
将（3，3）代入得，k=1，
，
当P与A重合时，即：PC=AC=8，由图像可知，把x=8代入y=x，y=8，
,
，
,
是BC的中点，

在Rt中，

故选：D．
【点睛】
本题考查了动点问题的函数图象，数形结合并熟练掌握三角形的面积计算公式与勾股定理是解题的关键．
5、C
【解析】
【分析】
求出正比函数的解析式，k值的绝对值表示车的速度；横轴上两个时间点的差表示乙走完全程所用时间，求出一次函数的解析式，确定它与正比例函数的交点坐标，横坐标即为二车相遇时间．
【详解】
设甲的解析式为y=kx，
∴6k=300,
解得k=50，
∴=50x，
∴甲车的速度为，
∴①正确；
∵乙晚出发2小时，
∴乙车用了5-2=3（h）到达城，
∴②错误；
设，
∴，
∴，
∴，
∵，
∴，
即甲行驶4小时，乙追上甲，
∴③正确；
故选C．
【点睛】
本题考查了待定系数法确定函数的解析式，函数图像，交点坐标的确定，解二元一次方程组，熟练掌握待定系数法，准确求交点的坐标是解题的关键．
6、A
【解析】
【分析】
根据题意作出合适的辅助线，可以先证明△ADC和△AOB的关系，即可建立y与x的函数关系，从而可以得到哪个选项是正确的．
【详解】
解：作AD∥x轴，作CD⊥AD于点D，如图所示，

由已知可得，OB=x，OA=1，∠AOB=90°，∠BAC=90°，AB=AC，点C的纵坐标是y，
∵AD∥x轴，
∴∠DAO+∠AOB=180°，
∴∠DAO=90°，
∴∠OAB+∠BAD=∠BAD+∠DAC=90°，
∴∠OAB=∠DAC，
在△OAB和△DAC中
，
∴△OAB≌△DAC（AAS），
∴OB=CD，
∴CD=x，
∵点C到x轴的距离为y，点D到x轴的距离等于点A到x的距离1，
∴y=x+1（x＞0）．
故选：A．
【点睛】
本题考查动点问题的函数图象，全等三角形的性质和判定，等腰三角形的定义．解题的关键是明确题意，建立相应的函数关系式，根据函数关系式判断出正确的函数图象．
7、D
【解析】
【分析】
根据统计表确定两个函数的增减性以及函数的交点，然后根据增减性判断．
【详解】
解：根据表可得y1＝kx+b中y随x的增大而增大；
y2＝mx+n中y随x的增大而减小，且两个函数的交点坐标是（﹣1，2）．
则当x＞﹣1时，kx+b＞mx+n．
故选：D．
【点睛】
本题考查了一次函数与一元一次不等式，一次函数的性质，正确确定增减性以及交点坐标是关键．
8、B
【解析】
【分析】
根据一次函数的图象是随的增大而减小，可得，再由，可得，即可求解．
【详解】
解：一次函数的图象是随的增大而减小，
∴ ，
；
又，
，
一次函数的图象经过第二、三、四象限．
故选：B
【点睛】
本题主要考查了一次函数的图象和性质，熟练掌握一次函数的图象和性质是解题的关键．
9、D
【解析】
【分析】
根据一次函数的图象与系数的关系，由一次函数图象分析可得m、n的符号，进而可得mn的符号，从而判断的图象是否正确，进而比较可得答案．
【详解】
A、由一次函数图象可知，，即，与正比例函数的图象可知，矛盾，故此选项错误；
B、由一次函数图象可知，，即，与正比例函数的图象可知，矛盾，故此选项错误；
C、由一次函数图象可知，，即；正比例函数的图象可知，矛盾，故此选项错误；
D、由一次函数图象可知，，即，与正比例函数的图象可知，故此选项正确；
故选：D．
【点睛】
此题主要考查了一次函数图象，注意：一次函数y=kx+b的图象有四种情况：①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限；②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限；③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限；④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限．
10、C
【解析】
【分析】
根据图象分别计算两船的速度判断A正确；利用图象计算出发5分钟时的距离差判断B正确；可疑船只出发5海里后快艇追赶，计算时间判断C错误正确；设快艇出发t分钟后追上可疑船只，列方程，求解即可判断D正确．
【详解】
解：快艇的速度为，可疑船只的速度为（海里/分），
∴快艇的速度比可疑船只的速度快0.5-0.2=0.3海里/分，故A选项不符合题意；
5分钟时快艇和可疑船只的距离为海里，故B选项不符合题意；
由图象可知：可疑船只出发5海里后快艇追赶，分钟=小时，故选项C符合题意；
设快艇出发t分钟后追上可疑船只，，解得t=，
这时离海岸海里，故D选项不符合题意；
故选：C．
【点睛】
此题考查了一次函数的图象，正确理解函数图象并得到相关信息进行计算是解题的关键．
二、填空题
1、21
【解析】
【分析】
根据题意设甲、乙、丙、丁车间的人数分别为人，甲、乙、丙、丁车间的日生产量分别为，则根据甲车间、丙车间的日生产之和比乙车间、丁车间的日生产之和少件，转化为只含有的方程，进而根据因式分解化简得，根据不等式求得的范围，根据是整数，即可求得的值，进而求得，根据题意列出代数式，并根据一次函数的性质求得当时，取得最大值，即可求得的值，即可解决问题．
【详解】
根据题意设甲、乙、丙、丁车间的人数分别为人，甲、乙、丙、丁车间的日生产量分别为，则
，，
，


即


又

即


即
解得

是整数，即是整数


设甲、丙两车间当日生产量之和为：
则

，则当最大时，取得最大值




即

时，取得最大值
此时
故答案为：21
【点睛】
本题考查了方程组的应用，一元一次不等式的应用，一次函数的性质求最值问题，理清题中各关系量是解题的关键．
2、100
【解析】
【分析】
由图象可知甲车从A地到地用了4小时，从地到地用小时，乙从地到地用了12小时，进而求得甲车的速度，A、两地的距离，乙车的速度，然后根据甲车到达地的时间求解乙车距A地的距离即可．
【详解】
解：由图象可知，甲车从A地到地用了4小时，从地到地用小时，乙从地到地用了12小时
∴甲车的速度是（千米时）
∴、两地之间的距离是千米
∴乙车的速度是（千米时）
∵甲车到达地时，用时4小时
∴此时乙车距A地（千米）
故答案为：100．
【点睛】
本题以行程问题为背景的函数图象的应用．解题的关键是根据函数图象理解题意，求得两车的速度．
3、
【解析】
【分析】
先求出y1，y2的值，再比较出其大小即可．
【详解】
解：∵点P1（3，y1）、P2（2，y2）在一次函数y=8x-1的图象上，
∴y1=8×3-1=23，y2=8×2-1=15，
∵23＞15，
∴y1＞y2．
故答案为：＞．
【点睛】
本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
4、x＜1
【解析】
【分析】
根据一次函数与一元一次不等式的关系即可求出答案．
【详解】
解：∵y=kx+b，kx+b＜0，
∴y＜0，
由图象可知：x＜1，
故答案为：x＜1．
【点睛】
本题考查一次函数与一元一次不等式，解题的关键是正确理解一次函数与一元一次不等式的关系，本题属于基础题型．
5、y=-0.5x+5
【解析】
【分析】
直接把点A（2，4）代入正比例函数y=kx，求出k的值即可；由A（2，4），AB⊥x轴于点B，可得出OB，AB的长，再由△ABO绕点A逆时针旋转90°得到△ADC，由旋转不变性的性质可知DC=OB，AD=AB，故可得出C点坐标，再把C点和A点坐标代入y=ax+b，解出解析式即可．
【详解】
解：∵正比例函数y=kx（k≠0）经过点A（2，4）
∴4=2k，
解得：k=2，
∴y=2x；
∵A（2，4），AB⊥x轴于点B，
∴OB=2，AB=4，
∵△ABO绕点A逆时针旋转90°得到△ADC，
∴DC=OB=2，AD=AB=4
∴C（6，2）
设直线AC的解析式为y=ax+b，
把（2，4）（6，2）代入解析式可得：，
解得：，
所以解析式为：y=-0.5x+5
【点睛】
本题考查的是一次函数图象上点的坐标特点及图形旋转的性质，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
三、解答题
1、一次函数的解析式为y＝x−4，与x轴交点的坐标是（4，0），与y轴的交点坐标是（0，−4）．
【解析】
【分析】
把x、y的值代入y＝kx−4，通过解方程求出k的值得到一次函数的解析式，根据直线与x轴相交时，函数的y值为0，与y轴相交时，函数的x值为0求出该直线与坐标轴的交点坐标．
【详解】
解：∵一次函数y＝kx−4，当x＝3时，y＝−1，
∴−1＝3k−4，解得k＝1，
∴一次函数的解析式为y＝x−4，
∵当y＝0时，x＝4，
当x＝0时，y＝−4，
∴该直线与x轴交点的坐标是（4，0），与y轴的交点坐标是（0，−4）．
【点睛】
本题考查了待定系数法求一次函数的解析式，一次函数与坐标轴的交点．正确求出直线的解析式是解题的关键．
2、 (1)0.5
(2)见解析
(3)（，），它的意义是当出发min后，乙离B的距离和甲离A地的距离都是km
【解析】
【分析】
（1）由甲骑车6min行驶了3km，可得甲骑车的速度是0.5km/min；
（2）设乙的速度为x km/min，求出乙的速度，可得乙出发后9min到达B地，即可作出图象；
（3）由y甲=0.5x，y乙=1.8-0.2x，可得两个函数图象的交点坐标为（，），它的意义是当出发min后，乙离B的距离和甲离A地的距离都是km．
(1)
解：甲骑车6min行驶了3km，
∴甲骑车的速度是3÷6=0.5（km/min），
故答案为：0.5；
(2)
解：设乙的速度为x km/min，由题意得
0.5×4-4x=1.2，
∴x=0.2，
又A、B两地相距3km，A、C两地相距1.2km，
∴B、C两地相距1.8km，
∴乙出发后1.8÷0.2=9（min）到达B地，
在同一平面直角坐标系中画出乙离B地的距离y乙（km）与所用时间x（min）的关系的大致图象如下：

(3)
解：由（1）（2）可知，y甲=0.5x，y乙=1.8-0.2x，
由0.5x=1.8-0.2x得x=，
当x=时，y甲=y乙=，
∴两个函数图象的交点坐标为（，），
它的意义是当出发min后，乙离B的距离和甲离A地的距离都是km．
【点睛】
本题考查一次函数的应用，一元一次方程的应用，解题的关键是读懂题意，求出甲、乙速度从而列出函数关系式．
3、 (1),
(2)见解析
【解析】
【分析】
（1）分别令，即可求得点的坐标；
（2）根据两点，作出一次函数的图象即可
(1)
令，则，即，
令，则，即
(2)
过，作直线的图象，如图所示，

【点睛】
本题考查了一次函数与坐标轴的交点问题，画一次函数图象，掌握一次函数的性质是解题的关键．
4、 (1)大货车用12辆，小货车用6辆
(2)（4≤x≤12，且x为整数）
(3)8辆大货车、2辆小货车前往A村；4辆大货车、4辆小货车前往B村．最少运费为1320元
【解析】
【分析】
（1）设大货车用a辆，小货车用b辆，根据大、小两种货车共18辆，运输168箱小鸡，列方程组求解；
（2）设前往A村的大货车为x辆，则前往B村的大货车为（12- x）辆，前往A村的小货车为（10- x）辆，前往B村的小货车为[6-（10-x）]辆，根据表格所给运费，求出y与x的函数关系式；
（3）结合已知条件，求x的取值范围，由（2）的函数关系式求使总运费最少的货车调配方案．
(1)
设大货车用a辆，小货车用b辆，根据题意得：
解得：．
∴大货车用12辆，小货车用6辆．
(2)
设前往A村的大货车为x辆，则前往B村的大货车为（12- x）辆，前往A村的小货车为（10- x）辆，前往B村的小货车为[6-（10-x）]辆，
y=80x+90（12-x）+40（10-x）+60[6-（10-x）]=10x+1240．

4≤x≤12，且x为整数．
（4≤x≤12，且x为整数）
(3)
由题意得：10x+8（10-x）≥96，解得：x≥8，
又∵4≤x≤12，
∴8≤x≤12且为整数，
∵y=10x+1240，k=10＞0，y随x的增大而增大，
∴当x=8时，y最小，
最小值为y=10×8+1240=1320（元）．
答：使总运费最少的调配方案是：8辆大货车、2辆小货车前往A村；4辆大货车、4辆小货车前往B村．最少运费为1320元．
【点睛】
本题考查了二元一次方程组的应用，一次函数的应用，一元一次不等式组的应用，理解题意列出方程组、关系式、不等式是解题的关键．
5、 (1)见解析
(2)
(3)6
【解析】
【分析】
（1）作出过点E的l的垂线即可解决；
（2）设直线l交x轴于点D，则由直线解析式可求得点D、点G的坐标，从而可得OD的长．由对称性及平行可得，设点P的坐标为(a，2a－2)，则可得点E的坐标，由及勾股定理可求得点的坐标；
（3）分别过点A、B作y轴的平行线，与过点G的垂直于y轴的直线分别交于点C、M，则点E在线段CM上运动，根据对称性知，点运动路径的长度等于CM的长，故只要求得CM的长即可，由A、B两点的坐标即可求得CM的长．
(1)
所作出点E的对应点E′如下图所示：

(2)
设直线l交x轴于点D
在y=2x－2中，令y=0，得x=1；令x=0，得y=－2
则点D、点G的坐标分别为(1，0)、(0，－2)
∴OD=1，OG=2
由对称性的性质得：，
∵GE∥x轴
∴
∴
∴
∴
设点P的坐标为(a，2a－2)，其中a>0，则可得点E的坐标为(a，－2)
∴EG=a
∴
∴
在Rt△中，由勾股定理得：
解得：
当时，
所以点P的坐标为

(3)
分别过点A、B作y轴的平行线，与过点G的垂直于y轴的直线分别交于点C、M，则点E在线段CM上运动，根据对称性知，点运动路径的长度等于CM的长
∵A，B两点的坐标分别为(－2，－6)，(4，6)
∴CM=4－(－2)=6
则点运动路径的长为6
故答案为：6

【点睛】
本题主要考查了一次函数的图象与性质、折叠的性质、尺规作图等知识，一次函数的性质及折叠的性质的应用是本题的关键．