









北师大版 (2019)第二章 平面向量及其应用6 平面向量的应用6.1 余弦定理与正弦定理完整版课件ppt
展开6.1 余弦定理与正弦定理
三、用余弦定理、正弦定理解三角形
第2课时 解三角形的实际应用举例
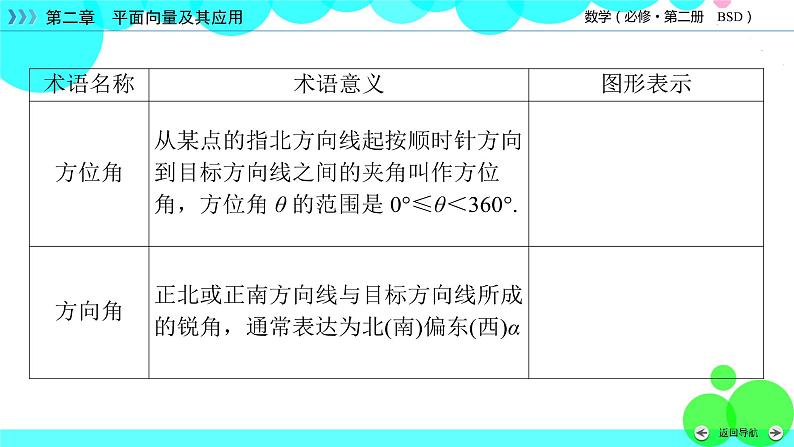
思考:仰角、俯角、方位角有什么区别?提示:三者的参照不同.仰角与俯角是相对水平线而言的,而方位角是相对于正北方向而言的.
利用余弦定理、正弦定理解决实际测量问题时,应具备的测量数据
1.辨析记忆(对的打“√”,错的打“×”)(1)从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为α=β.( )(2)若点P在点Q的北偏东44°,则点Q在点P的东偏北46°.( )(3)方位角大小范围是[0,π).( )[解析] (1)仰角与俯角是相对的,它们是平行线内错角.(2)若点P在点Q的北偏东44°,则点Q在点P的南偏西44°.(3)方位角范围为[0,2π).
2.如图,为了测量障碍物两侧A、B之间的距离,给定下列四组数据,测量时应该用的数据为( )A.α,a,bB.α,β,aC.a,b,γD.α,β,b
(1)如图,为了测量河的宽度,在一岸边选定两点A,B,望对岸的标记物C,测得∠CAB=30°,∠CBA=75°,AB=120 m,则河的宽度是______m.
[归纳提升] 测量距离的基本类型及方案
【对点练习】❶ (1)如图所示,A,B两点在一条河的两岸,测量者在A的同侧,且B点不可到达,测量者在A点所在的岸边选定一点C,测出AC=60 m,∠BAC=75°,∠BCA=45°,则A,B两点间的距离为_________.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两点C与D.现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.
[归纳提升] 测量高度问题的解题策略(1)“空间”向“平面”的转化:测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.(2)“解直角三角形”与“解斜三角形”结合,全面分析所有三角形,仔细规划解题思路.
2.某兴趣小组为了测量塔的高度,如图所示,在地面上一点A处测得塔顶B的仰角为60°,在塔底C处测得A处的俯角为45°.已知山岭高CD为36米,则塔高 BC为( )
4.如图,线段AB,CD分别表示甲、乙两楼,AB⊥BD,CD⊥BD,从甲楼顶部A处测得乙楼顶部C处的仰角为α=30°,测得乙楼底部D的俯角β=60°,已知甲楼高AB=24米,则乙楼高CD=______米.
5.某地电信局信号转播塔建在一山坡上,如图所示,施工人员欲在山坡上A,B两点处测量与地面垂直的塔CD的高,由A,B两地测得塔顶C的仰角分别为60°和45°,又知AB的长为40 m,斜坡与水平面成30°角,求该转播塔的高度.
北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理试讲课ppt课件: 这是一份北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理试讲课ppt课件,文件包含261余弦定理与正弦定理-用余弦定理正弦定理解三角形第三课时-高一数学同步教学课件pptx、261余弦定理与正弦定理-用余弦定理正弦定理解三角形第三课时-高一数学同步练习含答案解析docx、261余弦定理与正弦定理-用余弦定理正弦定理解三角形第三课时-高一数学同步练习docx等3份课件配套教学资源,其中PPT共55页, 欢迎下载使用。
数学必修 第二册1.6 解三角形一等奖课件ppt: 这是一份数学必修 第二册1.6 解三角形一等奖课件ppt,共19页。PPT课件主要包含了学习目标,新知学习,测量问题,典例剖析,测量距离问题,测量高度问题,测量角度问题等内容,欢迎下载使用。
高中数学湘教版(2019)必修 第二册1.6 解三角形评优课课件ppt: 这是一份高中数学湘教版(2019)必修 第二册1.6 解三角形评优课课件ppt,共47页。PPT课件主要包含了学习目标,新知学习,解三角形,余弦定理,正弦定理,典例剖析等内容,欢迎下载使用。













