北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理试讲课ppt课件

这是一份北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理试讲课ppt课件，文件包含261余弦定理与正弦定理-用余弦定理正弦定理解三角形第三课时-高一数学同步教学课件pptx、261余弦定理与正弦定理-用余弦定理正弦定理解三角形第三课时-高一数学同步练习含答案解析docx、261余弦定理与正弦定理-用余弦定理正弦定理解三角形第三课时-高一数学同步练习docx等3份课件配套教学资源，其中PPT共55页， 欢迎下载使用。

第二章 平面向量及其应用
高中/数学/北师大版（2019）/必修第二册
6.1 余弦定理与正弦定理-用余弦定理、正弦定理解三角形
温故知新
引入新课
在三角形的三条边和三个角这6个元素中,如果已知3个(至少含一边长),那么由余弦定理和正弦定理,就可以求得其他3个元素.具体情形如下:情形1　已知两个角的大小与一条边的边长.先由三角形内角和等于180°求出第三个角的大小,然后依据正弦定理求得另外两条边的边长.情形2　已知两条边的边长及其夹角的大小.先由余弦定理求出第三条边的边长,然后再由余弦定理求得第二、第三个角的大小.
一、用余弦定理、正弦定理解三角形
情形3　已知三条边的边长.由余弦定理求出两个角,再利用三角形内角和等于180°求出第三个角.情形4　已知两条边的边长和其中一边对角的大小.首先,由正弦定理求出第二条边所对角的正弦,这时,要判断是两解、一解还是无解.然后,根据三角形内角和等于180°得到第三个角的大小.最后,由余弦定理或正弦定理求得第三条边的边长.
思考1：应用正弦定理可以解决怎样的解三角形问题?提示：(1)已知三角形的任意两个角与一边,求其他两边和另一角.(2)已知三角形的两边与其中一边的对角,求另一边的对角,进而计算出其他的边和角.思考2：应用余弦定理可以解决哪些解三角形问题?提示：(1)已知三角形的两边及其夹角,求其他的边和角.(2)已知三角形的三边,求三个角.
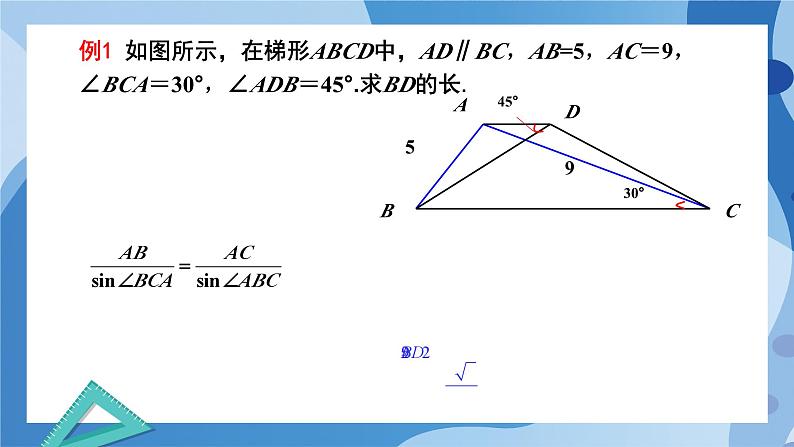
例1 如图所示，在梯形ABCD中，AD∥BC，AB=5，AC＝9，∠BCA＝30°，∠ADB＝45°.求BD的长.
例2 一次机器人足球比赛中,甲队1号机器由点A开始作匀速直线运动,到达B点时,发现足球在点D处正以2倍于自己的速度向点A作匀速直线滚动.如图,已知若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球?
分析 机器人最快截住足球的地方正是机器人与足球同时到达的地方,设为C点.利用速度建立AC与BC之间的关系,再利用余弦定理便可建立方程解决问题.
解.设机器人最快可在C处截住足球,点C在线段AD上.设BC=x dm,由题意,CD=2x dm.
C
AC=AD-CD=(17-2x) dm.
在△BCD中,由余弦定理,得.
即
解得
所以
(不合题意,舍去)
答 该机器人最快可在线段AD上离点A7dm的点C处截住足球.
例3:已知△ABC的角A,B,C所对的边分别是a,b,c,向量m=(a,b),n=(sinB,sinA),p=(b-c,a-c).⑴若m∥n,求证:△ABC为等腰三角形;⑵若m⊥p,c=2,C=60°,求△ABC的面积.
例3:已知△ABC的角A,B,C所对的边分别是a,b,c,向量m=(a,b),n=(sinB,sinA),p=(b-c,a-c).⑴若m∥n,求证:△ABC为等腰三角形;⑵若m⊥p,c=2,C=60°,求△ABC的面积.
解三角形常见题型
题型一： 正弦定理、余弦定理的使用
变式 1．(2011 年上海)在相距 2 千米的 A，B 两点处测量目标 C，若∠CAB＝75°，∠CBA＝60°，求 A，C 两点之间的距离．
例2：在△ABC 中，若 2cosBsinA＝sin ，试判断CABC 的形
状．
(2)边角转化的工具主要是正弦定理和余弦定理．
(1)三角形的形状按边分类主要有：等腰三角形，等边三角形等；按角分类主要有：直角三角形，锐角三角形，钝角三角形等．
>
题型二 判断三角形的形状
变式
1．在△ABC 中，sinA＝
sinB＋sinCcosB＋cosC
，试判断这个三角形的形状．
如图，在△ABC中，已知，B＝45°，D是BC边上的一点，AD＝5，AC＝7，DC＝3，求AB的长．
【例2】
题型二　计算线段的长度
如图，在△ABC中，已知，B＝45°，D是BC边上的一点，AD＝5，AC＝7，DC＝3，求AB的长．
【例3】
题型三　计算线段的长度
已知AB⊥BD，AC⊥CD，AC＝1，AB＝2，∠BAC＝120°，求BD的长．
变式
已知AB⊥BD，AC⊥CD，AC＝1，AB＝2，∠BAC＝120°，求BD的长．
例4.在△ABC中,角A、B、C的对边分别为a、b、c， 已知a+b=5，c= ，且 (1)求角C的大小； (2)求△ABC的面积. 解 （1）∵A+B+C=180°,
题型四　计算三角形面积
即7=a2+b2-ab,∴7=(a+b)2-3ab，由条件a+b=5,得7=25-3ab,ab=6,
正余弦定理的实际应用
(2)基本思路：
实际问题
数学模型
数学模型的解
实际问题的解
2.实际问题中的有关术语、名称 (1)仰角和俯角 在视线和水平线所成的较重，视线在水平线上方的角角仰角，在水平线下方的角俯角（如下图）.
仰角
俯角
④检验：检验上述所求的结果是否具有实际意义从而得出实际问题的解.
(2)方位角从正北方向顺时针转到目标方向线的夹角，如B点的方位角为α（如下图①）
(3)方向角①正南方向：从原点O出发的经过目标射线与正南的方向线重合，即目标在正南的方向线上.依次可类推正北方向、正东方向和正西方向.
②东南方向：指经过目标的涉嫌是正东和正南的夹角平分线（如图②）.③北偏东α：从正北向正东方向旋转α角度（图③）④南偏西β：从正南向正西方向旋转β角度（图④）
例1 自动卸货汽车采用液压机构.设计时需要计算油泵顶杆BC的长度（如图所示）.已知车箱最大仰角为60(指车厢AC与水平线夹角),油泵顶点B与车箱支点A之间的距离为1.95m,AB与水平线之间的夹角为620，AC长为1.40m,计算BC的长度(结果精确到0.01m).
分析
解：由余弦定理，得
BC2=
=3.571
∴BC≈1.89(m)．
答：顶杆BC约长1.89m．
AB2+AC2-2AB·ACcosA
例2.如图，两点C，D与烟囱底部在同一水平直线上,在点C1，D1利用高1.5m的测角仪器, 测得烟囱的仰角分别是 ＝450和 ＝600, ＣＤ间的距离是12m.求烟囱的高AB (结果精确到0.01m).


B
A
A1
C1
D1
解 在△BC1D1中, ∠BD1C1=180O -60O=120O, ∠C1BD1=60O -45O=15O,由正弦定理,得
从而
因此
1.我军有A、B两个小岛相距10海里，敌军在C岛，从A岛望C岛和B岛成60°的视角，从B岛望C岛和A岛成75°的视角，为提高炮弹命中率，须计算B岛和C岛间的距离，请你算算看。
A
C
B

如图，明明在底面上观测气球C，在A点处测得角 ，然后他向气球方向前进了50m到达B点处，此时仰角为 。若明明眼睛离地面1.6m,求气球的高度（精确到0.1m)
解
B D
C
A
由正弦定理，得
所以，气球的高度约是64.9+1.6=66.5（m)
（加上身高1.6m）
[针对训练]
[针对训练]
实际问题
抽象概括
演算
解三角形
实际问题的解
还原说明
示意图
构造三角形
小 结
成功的花，人们只惊慕她现时的明艳！然而当初它的芽儿，浸透了奋斗的泪泉，洒遍了牺牲的血雨。
谢谢观看