初中数学沪教版 (五四制)七年级下册第十五章 平面直角坐标系综合与测试单元测试一课一练

这是一份初中数学沪教版 (五四制)七年级下册第十五章 平面直角坐标系综合与测试单元测试一课一练，共30页。试卷主要包含了已知点A，点P关于y轴对称点的坐标是．，根据下列表述，能确定位置的是等内容，欢迎下载使用。
七年级数学第二学期第十五章平面直角坐标系单元测试
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、点P的坐标为（﹣3，2），则点P位于（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2、在平面直角坐标系中，点关于原点对称的点的坐标是（ ）
A． B． C． D．
3、若点P（m，1）在第二象限内，则点Q（1﹣m，﹣1）在（　　）
A．第四象限 B．第三象限 C．第二象限 D．第一象限
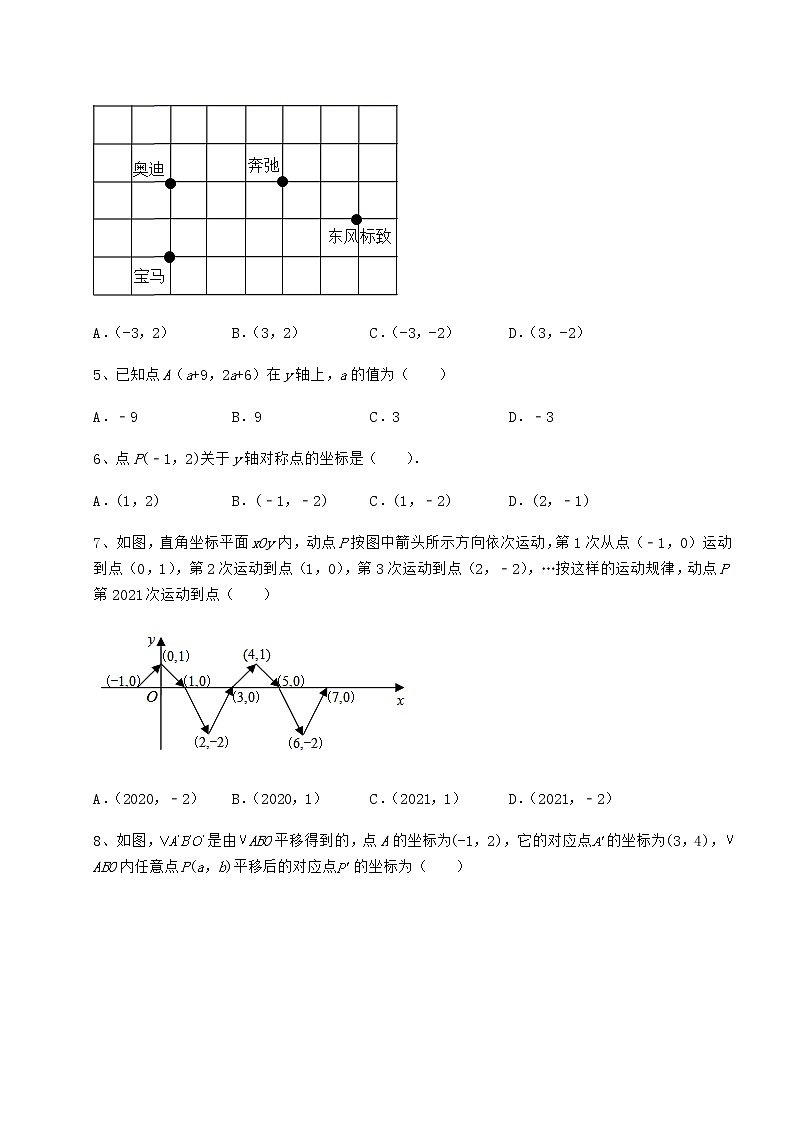
4、如图为某停车场的平面示意图，若“奥迪”的坐标是（-2，-1），“奔驰”的坐标是（1，-1），则“东风标致”的坐标是（ ）

A．（-3，2） B．（3，2） C．（-3，-2） D．（3，-2）
5、已知点A（a+9，2a+6）在y轴上，a的值为（　　）
A．﹣9 B．9 C．3 D．﹣3
6、点P(﹣1，2)关于y轴对称点的坐标是（　　）．
A．(1，2) B．(﹣1，﹣2) C．(1，﹣2) D．(2，﹣1)
7、如图，直角坐标平面xOy内，动点P按图中箭头所示方向依次运动，第1次从点（﹣1，0）运动到点（0，1），第2次运动到点（1，0），第3次运动到点（2，﹣2），…按这样的运动规律，动点P第2021次运动到点（ ）

A．（2020，﹣2） B．（2020，1） C．（2021，1） D．（2021，﹣2）
8、如图，是由ABO平移得到的，点A的坐标为(-1，2)，它的对应点的坐标为(3，4)，ABO内任意点P(a，b)平移后的对应点的坐标为（ ）

A．(a，b) B．(-a，-b) C．(a+2，b+4) D．(a+4，b+2)
9、根据下列表述，能确定位置的是（ ）
A．光明剧院8排 B．毕节市麻园路
C．北偏东40° D．东经116.16°，北纬36.39°
10、已知点A（n，3）在y轴上，则点B（n-1，n+1）在第（）象限
A．四 B．三 C．二 D．一
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
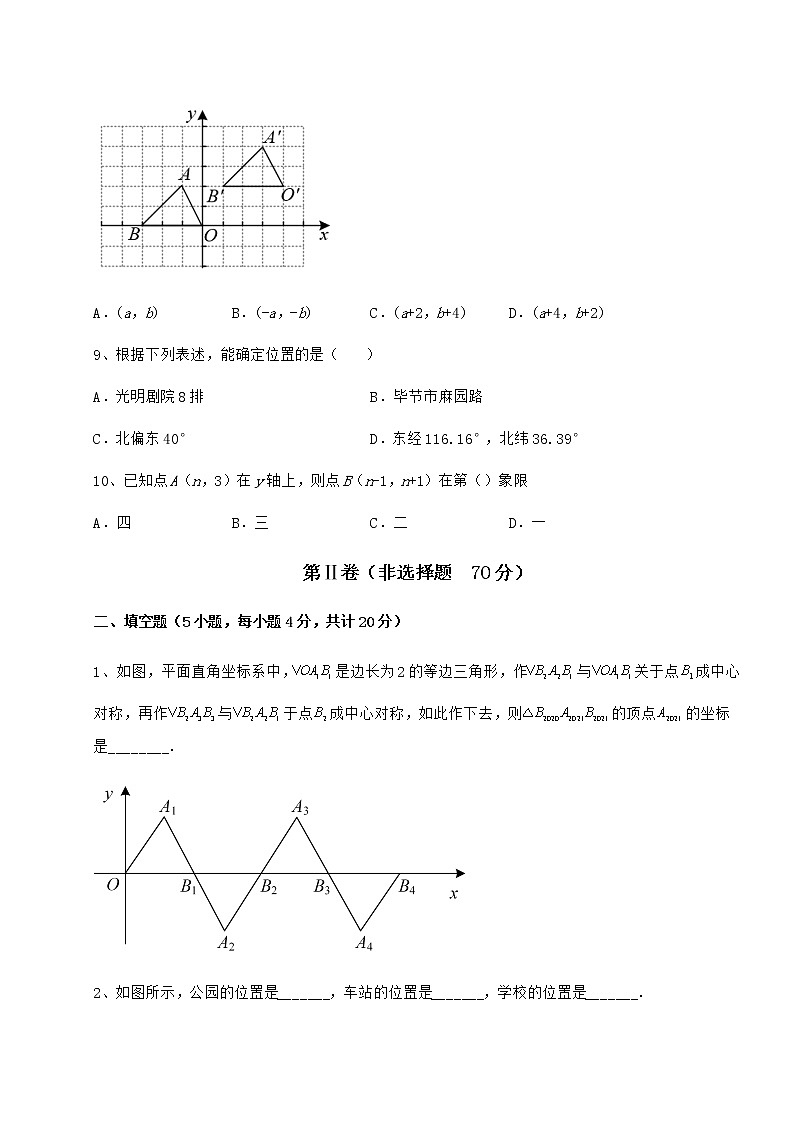
1、如图，平面直角坐标系中，是边长为2的等边三角形，作与关于点成中心对称，再作与于点成中心对称，如此作下去，则的顶点的坐标是________．

2、如图所示，公园的位置是_______，车站的位置是_______，学校的位置是_______．

3、在平面直角坐标系中，与点(2，-7)关于y轴对称的点的坐标为____．
4、已知点A（1，3）和B（1，－3），则点A，B关于________对称．
5、在平面直角坐标系中，点（－2，5）关于原点对称的点的坐标是___________．
三、解答题（10小题，每小题5分，共计50分）
1、在如图所示的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在正方形网格的格点（网格线的交点）上．
（1）请在如图所示的网格平面内作出平面直角坐标系，使点A坐标为（1 ，3），点B坐标为（2 ，1）；
（2）请画出△ABC关于y轴对称的图形△A1B1C1，并写出点B1的坐标为 　 　；
（3）P为y轴上一点，当PB+PC的值最小时，P点的坐标为 ．

2、如图，在直角坐标系中按要求作图，所画图形的顶点必须与每个小正方形的顶点重合．

（1）画出一个面积等于9的等腰直角三角形ABC，使△ABC的三个顶点在坐标轴上，且△ABC关于y轴对称，其中点A的坐标为(0，3)；（点B在点C的左侧）
（2）将△ABC向下平移3个单位，再向右平移1个单位得到△A1B1C1（点A、B、C的对应点分别为点A1、B1、C1），画出△A1B1C1，并直接写出A1C的长．
3、如图，在平面直角坐标系中，直角的三个顶点分别是，，．
（1）将以点为旋转中心顺时针旋转，画出旋转后对应的并写出各个顶点坐标；
（2）分别连结，后，求四边形的面积．

4、如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（3，2）．
（1）将△ABC向下平移四个单位长度，画出平移后的△A1B1C1；（点A、B、C的对应点分别是点A1、B1、C1）；
（2）画出△A1B1C1关于y轴对称的△A2B2C2（点A1、B1、C1的对称点分别是点A2、B2、C2）．

5、如图，在平面直角坐标系中，三个顶点的坐标为、、．

（1）在图中作出关于轴的对称图形；
（2）请直接写出点的坐标___________；
（3）在轴上画出一点使的值最小．
6、在如图所示的正方形网格中建立平面直角坐标系，的顶点坐标分别为，，，请按要求解答下列问题：
（1）画出关于x轴对称的，并写出点A的对应点的坐标为（ ， ）；
（2）平行于y轴的直线l经过，画出关于直线l对称的图形，并直接写出（ ， ），（ ， ），（ ， ）；
（3）仅用无刻度直尺作出的角平分线BD，保留画图痕迹（不写画法）．

7、在平面直角坐标系xOy中，点M(2，t-2)与点N关于过点(0，t)且垂直于y轴的直线对称．
（1）当t =-3时，点N的坐标为 ；
（2）以MN为底边作等腰三角形MNP．
①当t =1且直线MP经过原点O时，点P坐标为 ；
②若MNP上所有点到x轴的距离都不小于a(a是正实数)，则t的取值范围是 (用含a的代数式表示)
8、如图，三角形的项点坐标分别为，，．

（1）画出三角形关于点的中心对称的，并写出点的坐标；
（2）画出三角形绕点顺时针旋转90°后的，并写出点的坐标．
9、如图，已知△ABC三个顶点的坐标分A（﹣3，2），B（﹣1，3），C（﹣2，1）．将△ABC先向右平移4个单位，再向下平移3个单位后，得到△A′B′C′，点A，B，C的对应点分别为A′、B′、C′．
（1）根据要求在网格中画出相应图形；
（2）写出△A′B′C′三个顶点的坐标．

10、如图，在平面直角坐标系中，已知点A（﹣1，5），B（﹣3，1）和C（4，0）．
（1）平移线段AB，使点A平移到点C，画出平移后所得的线段CD，并写出点D的坐标；
（2）将线段AB绕点A逆时针旋转90°，画出旋转后所得的线段AE，并写出点E的坐标；
（3）线段MN与线段AB关于原点成中心对称，点A的对应点为点M，
①画出线段MN并写出点M的坐标；
②直接写出线段MN与线段CD的位置关系．


-参考答案-
一、单选题
1、B
【分析】
根据平面直角坐标系中四个象限中点的坐标特点求解即可．
【详解】
解：∵点P的坐标为（﹣3，2），
∴则点P位于第二象限．
故选：B．
【点睛】
此题考查了平面直角坐标系中四个象限中点的坐标特点，解题的关键是熟练掌握平面直角坐标系中四个象限中点的坐标特点：第一象限横坐标为正，纵坐标为正；第二象限横坐标为负，纵坐标为正；第三象限横坐标为负，纵坐标为负；第四象限横坐标为正，纵坐标为负．
2、A
【分析】
关于原点成中心对称的两个点的坐标规律：横坐标与纵坐标都互为相反数，根据原理直接作答即可.
【详解】
解：点关于原点对称的点的坐标是：
故选A
【点睛】
本题考查的是关于原点成中心对称的两个点的坐标规律，掌握“关于原点成中心对称的两个点的坐标规律：横坐标与纵坐标都互为相反数”是解题的关键.
3、A
【分析】
直接利用第二象限内点的坐标特点得出m的取值范围进而得出答案．
【详解】
∵点P（m，1）在第二象限内，
∴m＜0，
∴1﹣m＞0，
则点Q（1﹣m，﹣1）在第四象限．
故选：A．
【点睛】
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
4、D
【分析】
由题意，先建立平面直角坐标系，确定原点的位置，即可得到“东风标致”的坐标．
【详解】
解：∵“奥迪”的坐标是（2，1），“奔驰”的坐标是（1，1），
∴建立平面直角坐标系，如图所示：

∴“东风标致”的坐标是（3，2）；
故选：D．
【点睛】
本题考查了坐标确定位置：平面坐标系中的点与有序实数对一一对应；记住平面内特殊位置的点的坐标特征．
5、A
【分析】
根据y轴上点的横坐标为0列式计算即可得解．
【详解】
解：∵点A（a+9，2a+6）在y轴上，
∴a+9=0，
解得：a=-9，
故选：A．
【点睛】
本题考查了点的坐标，熟记y轴上点的横坐标为0是解题的关键．
6、A
【分析】
平面直角坐标系中任意一点P（x，y），关于y轴的对称点的坐标是（-x，y），即关于纵轴的对称点，纵坐标不变，横坐标变成相反数；这样就可以求出A的对称点的坐标，从而可以确定所在象限．
【详解】
解：∵点P（-1，2）关于y轴对称，
∴点P（-1，2）关于y轴对称的点的坐标是（1，2）．
故选：A．
【点睛】
本题主要考查了平面直角坐标系中关于坐标轴成轴对称的两点的坐标之间的关系．是需要识记的内容．
7、B
【分析】
观察图形可知，每4次运动为一个循环组循环，并且每一个循环组向右运动4个单位，用2021除以4，然后根据商和余数的情况确定运动后点的坐标即可．
【详解】
解：点的运动规律是每运动四次向右平移四个单位，
，
动点第2021次运动时向右个单位，
点此时坐标为，
故选：B．
【点睛】
本题主要考查平面直角坐标系下的规律探究题，解答时注意探究动点的运动规律，又要注意动点的坐标的象限符号．
8、D
【分析】
根据点A的坐标和点的坐标确定平移规律，即可求出点P(a，b)平移后的对应点的坐标．
【详解】
解：∵△A′B′O′是由△ABO平移得到的，点A的坐标为(-1，2)，它的对应点A′的坐标为(3，4)，
∴△ABO平移的规律是：先向右移4个单位长度，再向上平移2个单位长度，
∴△ABO内任意点P(a，b)平移后的对应点P′的坐标为(a+4，b+2)．
故选：D．
【点睛】
此题考查了平面直角坐标系中点的平移规律，解题的关键是熟练掌握平面直角坐标系中点的平移规律．点向左平移，点的横坐标减小，纵坐标不变；向右平移，点的横坐标增大，纵坐标不变；点向上平移，点的横坐标不变，纵坐标增大；向下平移，点的横坐标不变，纵坐标减小．
9、D
【分析】
根据位置的确定需要两个条件对各选项分析判断即可得解．
【详解】
解：．光明剧院8排，没有明确具体位置，故此选项不合题意；
．毕节市麻园路，不能确定位置，故此选项不合题意；
．北偏东，没有明确具体位置，故此选项不合题意；
．东经，北纬，能确具体位置，故此选项符合题意；
故选：D．
【点睛】
本题考查了坐标确定位置，解题的关键是理解位置的确定需要两个条件．
10、C
【分析】
直接利用y轴上点的坐标特点得出n的值，进而得出答案．
【详解】
解：∵点A（n，3）在y轴上，
∴n=0，
则点B（n-1，n+1）为：（-1，1），在第二象限．
故选：C．
【点睛】
本题主要考查了点的坐标，正确得出n的值是解题关键．
二、填空题
1、
【分析】
首先根据△是边长为2的等边三角形，可得的坐标为，的坐标为；然后根据中心对称的性质，分别求出点、、的坐标各是多少；最后总结出的坐标的规律，求出的坐标是多少即可．
【详解】
解：△是边长为2的等边三角形，
的坐标为：，的坐标为：，
△与△关于点成中心对称，
点与点关于点成中心对称，
，，
点的坐标是：，
△与△关于点成中心对称，
点与点关于点成中心对称，
，，
点的坐标是：，
△与△关于点成中心对称，
点与点关于点成中心对称，
，，
点的坐标是：，
，
，，，，，
的横坐标是：，的横坐标是：，
当为奇数时，的纵坐标是：，当为偶数时，的纵坐标是：，
顶点的纵坐标是：，
△是正整数）的顶点的坐标是：，
△的顶点的横坐标是：，纵坐标是：，
故答案为：．
【点睛】
此题主要考查了中心对称的性质、坐标与图形性质、等边三角形的性质等知识；熟练掌握等边三角形的性质和中心对称的性质，分别判断出的横坐标和纵坐标是解题的关键．
2、 (4，4)； (-2，-3)； (4，-2)
【分析】
用点坐标表示位置．
【详解】
①在直角坐标系中查横坐标为，纵坐标为；得到公园的位置为
故答案为：．
②在直角坐标系中查横坐标为，纵坐标为；得到车站的位置为
故答案为：．
③在直角坐标系中查横坐标为，纵坐标为；得到学校的位置为
故答案为：．
【点睛】
本题考察了坐标系中点的坐标．解题的关键在于正确的找出横、纵坐标的值．
3、（-2，-7）
【分析】
根据“关于y轴对称的点，纵坐标相同，横坐标互为相反数”解答即可．
【详解】
解：点（2，-7）关于y轴对称的点的坐标是（-2，-7）．
故答案为：（-2，-7）．
【点睛】
解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．
4、x轴
【分析】
根据点坐标关于轴对称的变换规律即可得．
【详解】
解：点坐标关于轴对称的变换规律：横坐标相同，纵坐标互为相反数．
点A（1，3）和B（1，－3），的横坐标相同，纵坐标互为相反数，
点关于轴对称，
故答案为：轴．
【点睛】
本题考查了点坐标与轴对称变化，熟练掌握点坐标关于轴对称的变换规律是解题关键．
5、（2，-5）
【分析】
根据平面直角坐标系中任意一点P（x，y），关于原点的对称点是（-x，-y）．
【详解】
解：根据中心对称的性质，得点P（-2，5）关于原点对称点的点的坐标是（2，-5）．
故答案为：（2，-5）．
【点睛】
本题主要考查了关于原点对称的点坐标的关系，是需要识记的基本问题．记忆方法是结合平面直角坐标系的图形记忆，比较简单．
三、解答题
1、（1）见详解；（2）△A1B1C1即为所求，见详解，（-2，1）；（3）（0，3）．
【分析】
（1）根据点A及点B的坐标，易得y轴在A的左边一个单位，x轴在A的下方3个单位，建立直角坐标系即可；
（2）根据平面直角坐标系求出点C坐标，根据ABC关于y轴对称的图形为△A1B1C1，求出A1(-1，3)，B1(-2，1)，C1（-4，7），描点A1(-1，3)，B1(-2，1)，C1（-4，7），再顺次连接即可画出ABC关于y轴对称的图形为△A1B1C1；
（3）过C1作y轴平行线与过B作x轴平行线交于G，BG交y轴于H，直接利用轴对称求最短路线的方法，根据点C的对称点为C1，连接BC1与y轴相交，此交点即为点P即可得出PB+PC的值最小，先证△GBC1为等腰直角三角形，再证△PHB为等腰直角三角形，最后求出y轴交点坐标即可．
【详解】
解：（1）点A坐标为（1 ，3），点B坐标为（2 ，1）
点A向左平移1个单位为y轴，再向下平移3个单位为x轴，建立如图平面直角坐标系，
如图所示：即为作出的平面直角坐标系；

（2）根据图形得出出点C（4，7）
∵△ABC关于y轴对称的图形△A1B1C1，关于y轴对称的点的特征是横坐标互为相反数，纵坐标不变，
∵A(1，3)，B (2，1)，C（4，7），
∴A1(-1，3)，B1(-2，1)，C1（-4，7），
在平面直角坐标系中描点A1(-1，3)，B1(-2，1)，C1（-4，7），
顺次连接A1B1， B1C1， C1 A1，
如图所示：△A1B1C1即为所求，
故答案为：（-2，1）；
（3）如图所示：点P即为所求作的点．过C1作y轴平行线与过B作x轴平行线交于G，BG交y轴于H，
∵点C的对称点为C1，
∴连接BC1与y轴相交于一点即为点P，此时PB+PC的值最小，
∵B（2，1），C1（-4，7），
∴C1G=7-1=6，BG=2-（-4）=6，
∴C1G=BG，
∴△GBC1为等腰直角三角形，
∴∠GBC1=45°，
∵∠OHB=90°，
∴△PHB为等腰直角三角形，
∴yP-1=2-0，
解得yP=3，
∴点P（0，3）．
故答案为（0，3）．

【点睛】
本题考查了建立平面直角坐标系，画轴对称图形，等腰直角三角形判定与性质，最短路径，掌握轴对称的性质及轴对称与坐标的变化规律并利用其准确作图，待定系数法求解析式是解答本题的关键．
2、（1）见解析；（2）画图见解析，A1C的长为4．
【详解】
解：（1）如图，△ABC即为所求．

∵AO=BO=CO=3，且AO⊥BC，
∴∠BAO=∠CAO=45°，△ABC的面积=BCAO=9，
∴∠BAC=90°，且△ABC关于y轴对称；
（2）如图，△A1B1C1即为所求．
如图，A1C的长为4．
【点睛】
本题考查了根据平移变换作图以及等腰直角三角形的判定和性质，解答本题的关键是根据网格结构作出对应点的位置，然后顺次连接．
3、（1）图见解析，，，；（2）9
【分析】
利用网格特点和旋转的性质画出、、的对应点、、，从而得到；
利用两个梯形的面积和减去一个三角形的面积计算四边形的面积．
【详解】
解：如图，为所作，各个顶点坐标为，，；

如图，四边形的面积．
【点睛】
本题考查了作图旋转变换，根据旋转的性质画出转后对应的是解决问题的关键．
4、（1）图见解析；（2）图见解析．
【分析】
（1）先根据平移分别画出点，再顺次连接即可得；
（2）先根据轴对称的性质画出点，再顺次连接即可得．
【详解】
解：（1）如图，即为所求；
（2）如图，即为所求．

【点睛】
本题考查了平移作图、画轴对称图形，熟练掌握平移和轴对称的作图方法是解题关键．
5、（1）见解析；（2）；（3）见解析
【分析】
（1）根据题意得：点、、关于轴的对称的的对应点分别为、、，再顺次连接，即可求解；
（2）根据和关于轴的对称图形，即可求解；
（3）作点 关于 轴的对称点 ，连接 交 轴于点 ，根据点 与 关于轴对称，可得，即可求解．
【详解】
解：根据题意得：点、、关于轴的对称的的对应点分别为、、，画出图形，如图所示：

（2）点的坐标为；
（3）如图，作点关于 轴的对称点 ，连接 交 轴于点 ，则点即为所求，

∵点 与 关于轴对称，
∴ ，
∴，
即当点 三点共线时，的值最小．
【点睛】
本题主要考查了坐标与图形，图形变换——轴对称，线段最短问题，熟练掌握若两点关于y轴对称，则横坐标互为相反数，纵坐标不变；若两点关于x轴对称，则横坐标不变，纵坐标互为相反数；两点间线段最短是解题的关键．
6、（1）图见解析，；（2）图见解析，，，；（3）见解析
【分析】
（1）利用关于x轴对称的点的坐标特征得到、、的坐标，然后描点即可；
（2）根据网格特点和对称的性质，分别作出A、B、C关于直线l的对称点、、，然后写出它们的坐标；
（3）把AB绕A点逆时针旋转90°得到AE，连接BE交AC于D．
【详解】
解：（1）如图，为所作，；
（2）如图，为所作，，，；
（3）如图，BD为所作．

【点睛】
本题考查了平面直角坐标系中点的坐标，画轴对称图形，解题的关键是正确写出点的坐标．
7、（1）(2，-1)；（2）①(-2，1)；②t≥a+2或t≤-a-2
【分析】
（1）先求出对称轴，再表示N点坐标即可；
（2）①以MN为底边作等腰三角形MNP，则点P在直线y=t=1上，直线OM与y=1的交点即为所求；
②表示出M、N、P的坐标，比较纵坐标的绝对值即可．
【详解】
（1）过点(0，t)且垂直于y轴的直线解析式为y=t
∵点M(2，t-2)与点N关于过点(0，t)且垂直于y轴的直线对称
∴可以设N点坐标为（2，n），且MN中点在y=t上
∴，记得
∴点N坐标为
∴当t =-3时，点N的坐标为
（2）①∵以MN为底边作等腰三角形MNP，且点M(2，t-2)与点N直线y=t对称．
∴点P在直线y=t上，且P是直线OM与y=1的交点
当t =1时M(2，-1)，N(2，3)
∴OM直线解析式为
∴当y=1时，
∴P点坐标为(-2，1)
②由题意得，点M坐标为(2，t-2)，点N坐标为，点P坐标为
∵，MNP上所有点到x轴的距离都不小于a
∴只需要或者
当M、N、P都在x轴上方时，，此时，解得t≥a+2
当MNP上与x轴有交点时，此时MNP上所有点到x轴的距离可以为0，不符合要求；
当M、N、P都在x轴下方时，，此时，解得t≤-a-2
综上t≥a+2或t≤-a-2
【点睛】
本题考查坐标与轴对称、等腰三角形的性质等知识，解题的关键是利用轴对称表示坐标，属于中考常考题型．
8、（1）图见解析，；（2）图见解析，
【分析】
（1）写出，，关于原点对称的点，，，连接即可；
（2）连接OC，OB，根据旋转的90°可得，，，，，即可；
【详解】
（1），，关于原点对称的点，，，作图如下；
（2）连接OC，OB，根据旋转的90°可得，，，，，，其中点C2的坐标是（3，-1），作图如下：

【点睛】
本题主要考查了平面直角坐标系中图形的旋转，作关于原点对称的图形，准确分析作图是解题的关键．
9、（1）见解析；（2），，
【分析】
（1）利用平移变换的性质分别作出，，的对应点，，即可．
（2）根据平面直角坐标系写出，，的坐标．
【详解】
解：（1）如图，△即为所求，

（2）根据平面直角坐标系可得：，，．
【点睛】
本题考查作图平移变换等知识，解题的关键是掌握平移变换的性质，属于中考常考题型．
10、（1）作图见解析，点D的坐标为（2，-4）；（2）作图见解析，点E的坐标为（3，3）；（3）①作图见解析，点M的坐标为（1，-5）；②MN∥CD．
【分析】
（1）根据点A平移到点C，即可得到平移的方向和距离，进而画出平移后所得的线段CD；
（2）根据线段AB绕点A逆时针旋转90°，即可画出旋转后所得的线段AE；
（3）①分别作出A，B的对应点M，N，连接即可；
②由平行线的传递性可得答案．
【详解】
解：（1）如图所示，线段CD即为所求，点D的坐标为（2，-4）；
（2）如图所示，线段AE即为所求，点E的坐标为（3，3）；

（3）①如图所示，线段MN即为所求，点M的坐标为（1，-5）；
②∵线段MN与线段AB关于原点成中心对称，
∴MN∥AB，
∵线段CD是由线段AB平移得到的，
∴CD∥AB，
∴MN∥CD．
【点睛】
本题主要考查了利用平移变换和旋转变换作图，解题的关键是理解题意，灵活运用所学知识解决问题．