初中北京课改版第十五章 四边形综合与测试课后作业题

这是一份初中北京课改版第十五章 四边形综合与测试课后作业题，共24页。试卷主要包含了下列图形中，是中心对称图形的是等内容，欢迎下载使用。
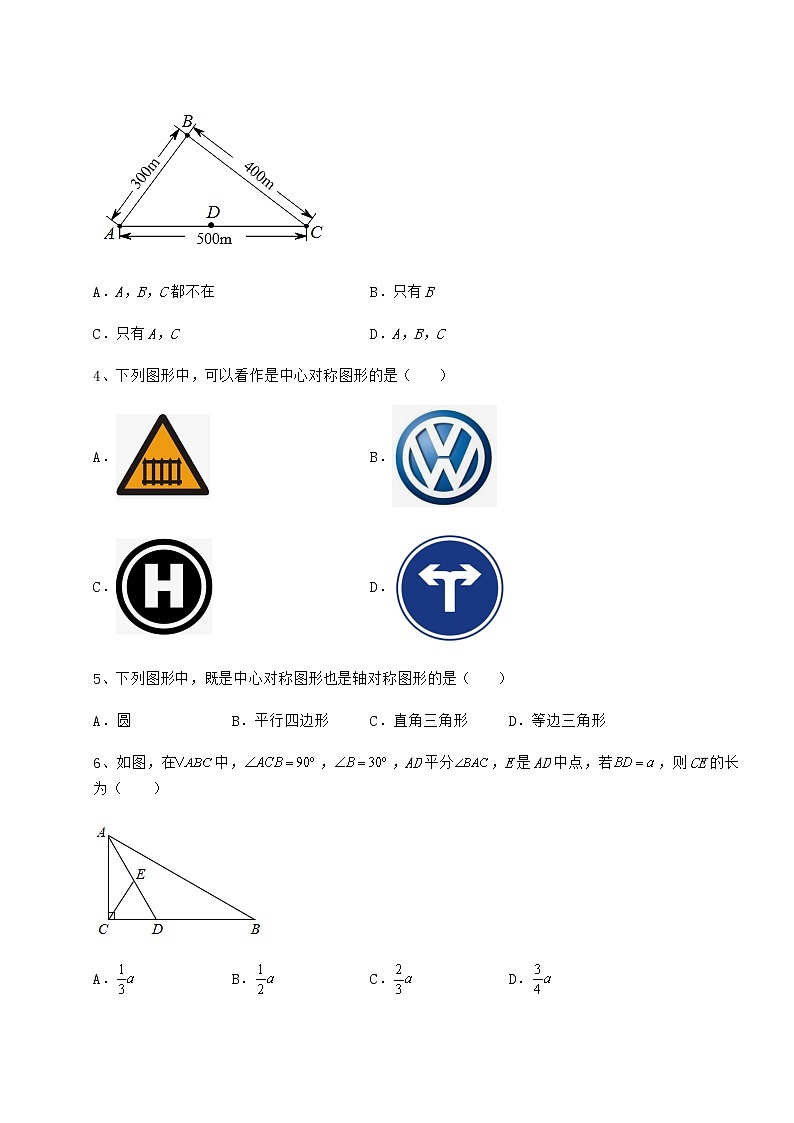
京改版八年级数学下册第十五章四边形定向攻克 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在六边形中，若，则（    ）A．180° B．240° C．270° D．360°2、平行四边形中，，则的度数是（    ）A． B． C． D．3、如图，A，B，C是某社区的三栋楼，若在AC中点D处建一个5G基站，其覆盖半径为300 m，则这三栋楼中在该5G基站覆盖范围内的是（    ）A．A，B，C都不在 B．只有BC．只有A，C D．A，B，C4、下列图形中，可以看作是中心对称图形的是（    ）A． B．C． D．5、下列图形中，既是中心对称图形也是轴对称图形的是（    ）A．圆 B．平行四边形 C．直角三角形 D．等边三角形6、如图，在中，，，AD平分，E是AD中点，若，则CE的长为（    ）A． B． C． D．7、下列图形中，是中心对称图形的是（    ）A． B． C． D．8、将一张长方形纸片ABCD按如图所示的方式折叠，AE、AF为折痕，点B、D折叠后的对应点分别为、，若＝10°，则∠EAF的度数为（　　）A．40° B．45° C．50° D．55°9、如图，在△ABC中，AC=BC=8，∠BCA=60°，直线AD⊥BC于点D，E是AD上的一个动点，连接EC，将线段EC绕点C按逆时针方向旋转60°得到FC，连接DF，则在点E的运动过程中，DF的最小值是（    ）A．1 B．1.5 C．2 D．410、如图，在正方形有中，E是AB上的动点，（不与A、B重合），连结DE，点A关于DE的对称点为F，连结EF并延长交BC于点G，连接DG，过点E作⊥DE交DG的延长线于点H，连接，那么的值为（ ）A．1 B． C． D．2第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，已知在矩形中，，，将沿对角线AC翻折，点B落在点E处，连接，则的长为_________．
 2、如图，正方形ABCD的边长为做正方形，使A，B，C，D是正方形各边的中点；做正方形，使是正方形各边的中点……以此类推，则正方形的边长为__________．             
 3、菱形的对角线之比为3：4，且面积为24，则它的对角线分别为________．4、如图，每个小正方形的边长都为1，△ABC是格点三角形，点D为AC的中点，则线段BD的长为 _____．5、在平面直角坐标系中，与点关于原点对称的点的坐标是________．三、解答题（5小题，每小题10分，共计50分）1、在中，，斜边，过点作，以AB为边作菱形ABEF，若，求的面积．2、如图，在等腰三角形ABC中，AB＝BC，将等腰三角形ABC绕顶点B按逆时针方向旋转角a到的位置，AB与相交于点D，AC与分别交于点E，F．（1）求证：BCF；（2）当C＝a时，判定四边形的形状并说明理由．3、如图，四边形ABCD是平行四边形，E，F是对角线AC的三等分点，连接BE，DF．证明BE=DF．4、如图是由3个同样的正方形所组成，请再补上一个同样的正方形，使得由4个正方形组成的图形成为一个中心对称图形．画出所有情况（给出的图形不一定全用，不够可添加）．5、如图，已知△ACB中，∠ACB＝90°，E是AB的中点，连接EC，过点A作AD∥EC，过点C作CD∥EA，AD与CD交于点D．（1）求证：四边形ADCE是菱形；（2）若AB＝8，∠DAE＝60°，则△ACB的面积为        （直接填空）． -参考答案-一、单选题1、C【分析】根据多边形外角和求解即可．【详解】解： ，  ，故选：C【点睛】本题考查了多边形的外角和定理，掌握多边形外角和是解题的关键．2、B【分析】根据平行四边形对角相等，即可求出的度数．【详解】解：如图所示，∵四边形是平行四边形，∴，∴，∴．故：B．【点睛】本题考查了平行四边形的性质，解题的关键是掌握平行四边形的性质．3、D【分析】根据三角形边长然后利用勾股定理逆定理可得为直角三角形，由直角三角形斜边上的中线性质即可得．【详解】解：如图所示：连接BD，∵，，，∴，∴为直角三角形，∵D为AC中点，∴，∵覆盖半径为300 ，∴A、B、C三个点都被覆盖，故选：D．【点睛】题目主要考查勾股定理逆定理，直角三角形斜边中线的性质等，理解题意，综合运用两个定理是解题关键．4、C【分析】根据中心对称图形的定义进行逐一判断即可．【详解】解：A、不是中心对称图形，故此选项不符合题意；B、不是中心对称图形，故此选项不符合题意；C、是中心对称图形，故此选项符合题意；D、不是中心对称图形，故此选项不符合题意；故选C．【点睛】本题主要考查了中心对称图形的识别，解题的关键在于能够熟练掌握中心对称图形的定义：把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．5、A【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A．圆既是中心对称图形也是轴对称图形，故此选项符合题意；B．平行四边形是中心对称图形，不是轴对称图形，故此选项不合题意；
C．直角三角形既不是中心对称图形，也不一定是轴对称图形，不符合题意；
D．等边三角形不是中心对称图形，是轴对称图形，故此选项不合题意．
故选：A．【点睛】本题考查中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180°后与原图重合．6、B【分析】根据三角形内角和定理求出∠BAC，根据角平分线的定义∠DAB=∠B，求出AD，根据直角三角形的性质解答即可．【详解】解：∵∠ACB=90°，∠B=30°，∴∠BAC=90°-30°=60°，∵AD平分∠BAC，∴∠DAB=∠BAC=30°，∴∠DAB=∠B，∴AD=BD=a，在Rt△ACB中，E是AD中点，∴CE=AD=，故选： B．【点睛】本题考查的是直角三角形的性质、角平分线的定义，掌握直角三角形斜边上的中线是斜边的一半是解题的关键．7、B【分析】根据中心对称图形的定义求解即可．【详解】解：A、不是中心对称图形，不符合题意；B、是中心对称图形，符合题意；C、不是中心对称图形，不符合题意；D、不是中心对称图形，不符合题意．故选：B．【点睛】此题考查了中心对称图形，解题的关键是熟练掌握中心对称图形的定义．中心对称图形：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．8、A【分析】可以设∠EAD′＝α，∠FAB′＝β，根据折叠可得∠DAF＝∠D′AF，∠BAE＝∠B′AE，用α，β表示∠DAF＝10°+β，∠BAE＝10°+α，根据四边形ABCD是矩形，利用∠DAB＝90°，列方程10°+β+β+10°+10°+α+α＝90°，求出α+β＝30°即可求解．【详解】解：设∠EAD′＝α，∠FAB′＝β，根据折叠性质可知：∠DAF＝∠D′AF，∠BAE＝∠B′AE，∵∠B′AD′＝10°，∴∠DAF＝10°+β，∠BAE＝10°+α，∵四边形ABCD是矩形∴∠DAB＝90°，∴10°+β+β+10°+10°+α+α＝90°，∴α+β＝30°，∴∠EAF＝∠B′AD′+∠D′AE+∠FAB′，＝10°+α+β，＝10°+30°，＝40°．则∠EAF的度数为40°．故选：A．【点睛】本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．9、C【分析】取线段AC的中点G，连接EG，根据等边三角形的性质以及角的计算即可得出CD=CG以及∠FCD=∠ECG，由旋转的性质可得出EC=FC，由此即可利用全等三角形的判定定理SAS证出△FCD≌△ECG，进而即可得出DF=GE，再根据点G为AC的中点，即可得出EG的最小值，此题得解．【详解】解：取线段AC的中点G，连接EG，如图所示．
∵AC=BC=8，∠BCA=60°，
∴△ABC为等边三角形，且AD为△ABC的对称轴，
∴CD=CG=AB=4，∠ACD=60°，
∵∠ECF=60°，
∴∠FCD=∠ECG，
在△FCD和△ECG中，，
∴△FCD≌△ECG（SAS），
∴DF=GE．
当EG∥BC时，EG最小，
∵点G为AC的中点，
∴此时EG=DF=CD=BC=2．
故选：C．【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质，三角形中位线的性质，解题的关键是通过全等三角形的性质找出DF=GE，本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边是关键．10、B【分析】作辅助线，构建全等三角形，证明△DAE≌△ENH，得AE=HN，AD=EN，再说明△BNH是等腰直角三角形，可得结论．【详解】解：如图，在线段AD上截取AM，使AM=AE，，  ∵AD=AB，∴DM=BE，∵点A关于直线DE的对称点为F，∴△ADE≌△FDE，∴DA=DF=DC，∠DFE=∠A=90°，∠1=∠2，∴∠DFG=90°，在Rt△DFG和Rt△DCG中，∵，∴Rt△DFG≌Rt△DCG（HL），∴∠3=∠4，∵∠ADC=90°，∴∠1+∠2+∠3+∠4=90°，∴2∠2+2∠3=90°，∴∠2+∠3=45°，即∠EDG=45°，∵EH⊥DE，∴∠DEH=90°，△DEH是等腰直角三角形，∴∠AED+∠BEH=∠AED+∠1=90°，DE=EH，∴∠1=∠BEH，在△DME和△EBH中，∵，∴△DME≌△EBH（SAS），∴EM=BH，Rt△AEM中，∠A=90°，AM=AE，∴，∴ ，即=．故选：B．【点睛】本题考查了正方形的性质，全等三角形的判定定理和性质定理，等知识，解决本题的关键是作出辅助线，利用正方形的性质得到相等的边和相等的角，证明三角形全等．二、填空题1、【分析】过点E作EF⊥AD于点F，先证明CG=AG，再利用勾股定理列方程，求出AG的值，结合三角形的面积法和勾股定理，即可求解．【详解】解：如图所示：过点E作EF⊥AD于点F，
 有折叠的性质可知：∠ACB=∠ACE，∵AD∥BC，∴∠ACB=∠CAD，∴∠CAD=∠ACE，∴CG=AG，设CG=x，则DG=8-x，∵在中，，∴x=5，∴AG=5，在中，EG=，EF⊥AD，∠AEG=90°，∴，∵在中，，、∴DF=8-=，∴在中，，故答案是：．【点睛】本题主要考查矩形的性质，折叠的性质，勾股定理，等腰三角形的判定定理，添加辅助线构造直角三角形，是解题的关键．2、【分析】利用正方形ABCD的及勾股定理，求出的长，再根据勾股定理求出和的长，找出规律，即可得出正方形的边长．【详解】解：∵A，B，C，D是正方形各边的中点∴，∵正方形ABCD的边长为，即AB=，∴，解得：，∴==2，同理==2，
==4  …，
∴，
∴=，∴的边长为
故答案为：．【点睛】本题考查了正方形性质、勾股定理的应用，解此题的关键是能根据计算结果得出规律，本题具有一定的代表性，是一道比较好的题目．3、6和8【分析】根据比例设两条对角线分别为3x、4x，再根据菱形的面积等于两对角线乘积的一半列式求出x的值即可．【详解】解：设两条对角线分别为3x、4x，根据题意得，×3x•4x=24，解得x=2（负值舍去），∴菱形的两对角线的长分别为，．故答案为：6和8．【点睛】本题考查了菱形的面积，主要利用了菱形的对角线互相垂直平分的性质，菱形的面积的求法，需熟记．4、##【分析】根据勾股定理列式求出AB、BC、AC，再利用勾股定理逆定理判断出△ABC是直角三角形，然后根据直角三角形斜边上的中线等于斜边的一半解答即可．【详解】解：，，，，∴∠ABC＝90°，∵点D为AC的中点，∴BD为AC边上的中线，∴BD＝AC，故答案为：【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理，勾股定理逆定理的应用，判断出△ABC是直角三角形是解题的关键．5、（-3，-1）【分析】由题意直接根据两个点关于原点对称时，它们的坐标符号相反进行分析即可得出答案.【详解】解：在平面直角坐标系中，与点关于原点对称的点的坐标是（-3，-1）.故答案为：（-3，-1）.【点睛】本题考查的是关于原点的对称的点的坐标，注意掌握平面直角坐标系中任意一点P（x，y），关于原点的对称点是（-x，-y），即关于原点的对称点，横纵坐标都变成相反数．三、解答题1、4【分析】分别过点E、C作EH、CG垂直AB,垂足为点H、G,则CG是斜边AB上的高；在菱形ABEF中， 利用平行线的性质不难得到CG=EH;菱形的对角相等，四条边相等，联系含30°角的直角三角形的性质求出EH,问题即可解答。【详解】解：如图，分别过作垂足为点 四边形ABEF为菱形，，，，在中， ，根据题意，，根据平行线间的距离处处相等， .答：的面积为４.【点睛】本题考查了菱形的性质，直角三角形的性质，平行线间的距离及三角形面积的计算，正确利用菱形的四边相等及直角三角形中，30角所对直角边是斜边的一半是解题的关键．2、（1）见解析；（2）菱形，见解析【分析】（1）根据等腰三角形的性质得到AB=BC，∠A=∠C，由旋转的性质得到A1B=AB=BC，∠A=∠A1=∠C，∠A1BD=∠CBC1，根据全等三角形的判定定理得到△BCF≌△BA1D；
（2）由（1）可知∠=∠=∠A=∠C=a,B=B=AB=BC通过证明∠FBC=∠可得 BC，利用∠EC=∠C=180°推出∠EC+∠=180°  得到BCE从而证明四边形为平行四边形再利用B=BC可证明四边形为菱形．【详解】（1）证明：∵等腰三角形ABC旋转角a得到∴∠BD=∠FBC=a∠=∠=∠A=∠C   B=B=AB=BC∴BCF（ASA）    （2）解：四边形为菱形理由：∵C=a由（1）可知∠=∠=∠A=∠C=a    B=B=AB=BC又∵ ∠BD=∠FBC=a ∴∠FBC=∠∴BC  ∴∠EC=∠C=180°∴∠EC+∠=180°  ∴BCE∴四边形为平行四边形又∵B=BC∴ 四边形为菱形【点睛】本题考查了旋转的性质，全等三角形的判定和性质，等腰三角形的性质，正确的理解题意是解题的关键．3、见详解【分析】由题意易得AB=CD，AB∥CD，AE=CF，则有∠BAE=∠DCF，进而问题可求证．【详解】证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠BAE=∠DCF，∵E，F是对角线AC的三等分点，∴AE=CF，在△ABE和△CDF中，，∴△ABE≌△CDF（SAS），∴BE=DF．【点睛】本题主要考查平行四边形的性质及全等三角形的性质与判定，熟练掌握平行四边形的性质及全等三角形的性质与判定是解题的关键．4、见解析【分析】根据中心对称图形的概念求解即可．中心对称图形：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．【详解】解：如图所示，一共有三种情况：【点睛】此题考查了画中心对称图形，解题的关键是熟练掌握中心对称图形的概念．中心对称图形：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形．5、（1）见解析；（2）【分析】（1）由AD//CE，CD//AE ，得四边形AECD为平行四边形，根据直角三角形斜边上中线性质，得CE=AE，可知四边形ADCE是菱形；（2）由菱形的性质可得当∠DAE=60°时，∠CAE=30°，可求BC，再根据勾股定理求出AC，最后求面积即可．【详解】解：（1）∵∥，∥，∴四边形是平行四边形．∵，是的中点，∴，∴四边形是菱形；（2）∵四边形是菱形，，∴．∵在Rt△中，，，，∴， ∴．∴．【点睛】此题主要考查了菱形的性质和判定，含30度角的直角三角形的性质，直角三角形斜边上的中线，勾股定理，三角形面积，能够灵活运用菱形知识解决有关问题是解题的关键．