2021年北京通州区觅子店中学九年级上期末数学试卷

这是一份2021年北京通州区觅子店中学九年级上期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 抛物线 y=−x2 开口方向是
A. 向上B. 向下C. 向左D. 向右

2. 二次函数 y=x+22−1 的图象的顶点坐标是
A. 2,−1B. −2,−1C. 2,1D. −2,1

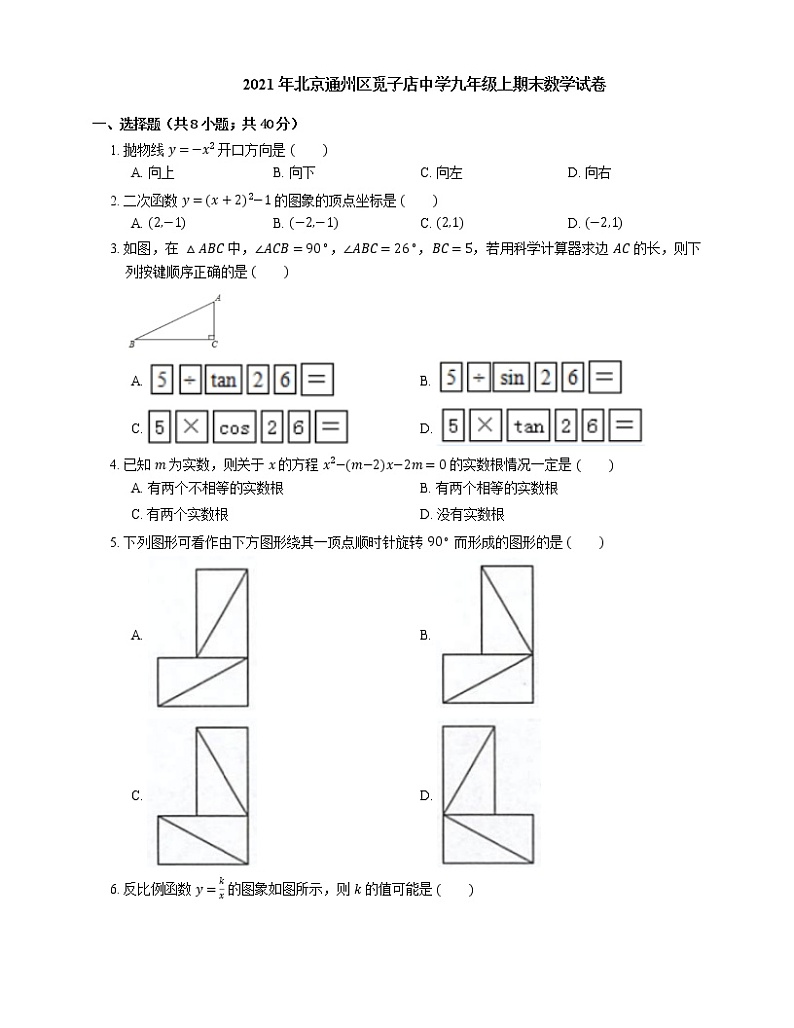
3. 如图，在 △ABC 中，∠ACB=90∘，∠ABC=26∘，BC=5，若用科学计算器求边 AC 的长，则下列按键顺序正确的是
A. B.
C. D.

4. 已知 m 为实数，则关于 x 的方程 x2−m−2x−2m=0 的实数根情况一定是
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 有两个实数根D. 没有实数根

5. 下列图形可看作由下方图形绕其一顶点顺时针旋转 90∘ 而形成的图形的是
A. B.
C. D.

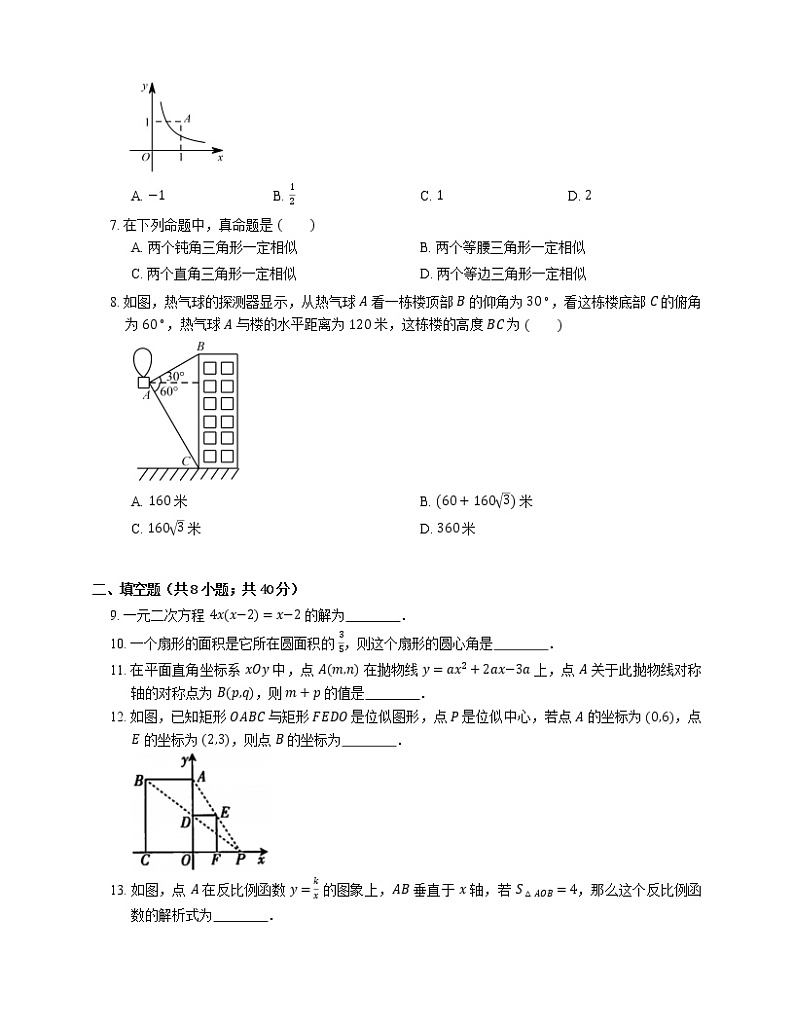
6. 反比例函数 y=kx 的图象如图所示，则 k 的值可能是
A. −1B. 12C. 1D. 2

7. 在下列命题中，真命题是
A. 两个钝角三角形一定相似B. 两个等腰三角形一定相似
C. 两个直角三角形一定相似D. 两个等边三角形一定相似

8. 如图，热气球的探测器显示，从热气球 A 看一栋楼顶部 B 的仰角为 30∘，看这栋楼底部 C 的俯角为 60∘，热气球 A 与楼的水平距离为 120 米，这栋楼的高度 BC 为
A. 160 米B. 60+1603 米
C. 1603 米D. 360 米

二、填空题（共8小题；共40分）
9. 一元二次方程 4xx−2=x−2 的解为 ．

10. 一个扇形的面积是它所在圆面积的 35，则这个扇形的圆心角是 ．

11. 在平面直角坐标系 xOy 中，点 Am,n 在抛物线 y=ax2+2ax−3a 上，点 A 关于此抛物线对称轴的对称点为 Bp,q，则 m+p 的值是 ．

12. 如图，已知矩形 OABC 与矩形 FEDO 是位似图形，点 P 是位似中心，若点 A 的坐标为 0,6，点 E 的坐标为 2,3，则点 B 的坐标为 ．

13. 如图，点 A 在反比例函数 y=kx 的图象上，AB 垂直于 x 轴，若 S△AOB=4，那么这个反比例函数的解析式为 ．

14. 若点 P2−m,3m+1 在坐标轴上，则点 P 的坐标为 ．

15. 如图，在 x 轴的正半轴上依次截取 OA1=A1A2=A2A3=A3A4=A4A5=⋯，分别过点 A1，A2，A3，A4，A5，⋯ 作 x 轴的垂线与反比例函数 y=2xx>0 的图象交于点 P1，P2，P3，P4，P5，⋯，得到 Rt△OP1A1，Rt△A1P2A2，Rt△A2P3A3，Rt△A3P4A4，Rt△A4P5A5，⋯，设其面积分别为 S1，S2，S3，S4，S5，⋯，则 S10= ．

16. 要把木条固定在墙上至少要钉 个钉子，这是因为 ．

三、解答题（共12小题；共156分）
17. 计算：0.25⋅cs60∘−2−3−10+tan60∘

18. 如图，在 Rt△ABC 中，∠ACB=90∘，CD⊥AB 于 D．
（1）图中有几对相似三角形?请写出并选择一对进行证明；
（2）若 AD=3，CD=6，求 BC 的长．

19. 已知 2 是方程 x2−c=0 的一个根，求常数 c 的值及该方程的另一根．

20. 甲、乙两地相距 400 km，如果把汽车从甲地到乙地所用的时间 yh 表示为汽车的平均速度 xkm/h 的函数．
（1）写出时间 yh 与平均速度 xkm/h 之间的函数表达式；
（2）若汽车的平均速度不超过 80km/h，则汽车从甲地到乙地所用的时间至少需要多少小时?

21. 下面是小飞设计的“过圆外一点作圆的切线”的尺规作图过程．
已知：如图，P 为 ⊙O 外一点．
求作：经过点 P 的 ⊙O 的切线．
作法：如下图，
①连接 OP，作线段 OP 的垂直平分线，交 OP 于点 A；
②以点 A 为圆心，OA 长为半径作圆，交 ⊙O 于 B，C 两点；
③作直线 PB，PC．
所以直线 PB，PC 就是所求作的切线．
根据小飞设计的尺规作图过程：
（1）使用直尺和圆规补全图形（保留作图痕迹）；
（2）完成下面的证明（说明：括号里填写推理的依据）
证明：如图，连接 OB，OC，
∵PO 为 ⊙A 的直径，
∴∠PBO=∠PCO= （ ）．
∴PB⊥OB，PC⊥OC．
∴PB，PC 为 ⊙O 的切线（ ）．

22. 已知二次函数 y=−x2+x+c 的图象与 x 轴只一个交点．
（1）求这个二次函数的表达式及顶点坐标；
（2）当 x 取何值时，y 随 x 的增大而减小．

23. 如图所示（左图为实景侧视图，右图为安装示意图），在屋顶的斜坡面上安装太阳能热水器：先安装支架 AB 和 CD（均与水平面垂直），再将集热板安装在 AD 上．为使集热板吸热率更高，公司规定：AD 与水平线夹角为 θ1，且在水平线上的射影 AF 为 1.4 m．现已测量出屋顶斜面与水平面夹角为 θ2，并已知 tanθ1=1.082，tanθ2=0.412．如果安装工人已确定支架 AB 高为 25 cm，求支架 CD 的高（结果精确到 1 cm）?

24. 如图①，某商场在一楼到二楼之间设有上，下行自动扶梯和步行楼梯．甲，乙两人从二楼同时下行，甲乘自动扶梯，乙走步行楼梯，甲离一楼地面的高度 h（单位：m）与下行时间 x（单位：s）之间具有函数关系 h=−310x+6，乙离一楼地面的高度 y（单位：m）与下行时间 x（单位：s）的函数关系如图②所示．
（1）求 y 关于 x 的函数解析式；
（2）请通过计算说明甲，乙两人谁先到达一楼地面．

25. 数学活动课上，老师提出问题：如图 1，在 Rt△ABC 中，∠C=90∘，BC=4 cm，AC=3 cm，点 D 是 AB 的中点，点 E 是 BC 上一个动点，连接 AE，DE．问 CE 的长是多少时，△AED 的周长等于 CE 长的 3 倍．
设 CE=x cm，△AED 的周长为 y cm（当点 E 与点 B 重合时，y 的值为 10）．小牧根据学习函数的经验，对函数 y 随自变量 x 的变化而变化的规律进行了探究．
下面是小牧的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了 x 与 y 的几组值，如下表：
（说明：补全表格时相关数值保留一位小数）
（2）建立平面直角坐标系，描出以上表中对应值为坐标的点，画出该函数的图象，如图 2；
（3）结合画出的函数图象，解决问题：
①当 CE 的长约为 cm 时，△AED 的周长最小；
②当 CE 的长约为 cm 时，△AED 的周长等于 CE 的长的 3 倍．

26. 如图，点 A，B 在 ⊙O 上，直线 AC 是 ⊙O 的切线，OC⊥OB，连接 AB 交 OC 于点 D．
（1）求证：AC=CD；
（2）若 AC=2，AO=5，求 OD 的长度．

27. P 为等边 △ABC 的边 AB 上一点，Q 为 BC 延长线上一点，且 PA=CQ，连 PQ 交 AC 边于 D．
（1）证明：PD=DQ．
（2）如图 2，过 P 作 PE⊥AC 于 E，若 AB=6，求 DE 的长．

28. 如图，在直角坐标系中，四边形 ABCO 是正方形，已知点 C 的坐标为 3,1．求点 A 和点 B 的坐标．
答案
第一部分
1. B【解析】∵a=−1<0，
∴ 抛物线的开口向下．
2. B【解析】∵y=x+22−1，
∴ 二次函数图象的顶点坐标为 −2,−1．
3. D【解析】由 tan∠B=ACBC，得 AC=BC⋅tanB=5×tan26．
4. C【解析】Δ=m−22−4×−2m=m+22．
对于任意实数 m，都有 m+22≥0，即 Δ≥0，
所以原方程一定有两个实数根．
5. B
6. B
7. D
8. C【解析】如图，过点 A 作 AD⊥BC 于点 D，
则 ∠BAD=30∘，∠CAD=60∘，AD=120（米），
在 Rt△ABD 中，BD=AD⋅tan30∘=120×33=403（米），
在 Rt△ACD 中，CD=AD⋅tan60∘=120×3=1203（米），
∴BC=BD+CD=1603（米）．
第二部分
9. x1=2，x2=14
【解析】4xx−2=x−2，
4xx−2−x−2=0，
x−24x−1=0，
x−2=0 或 4x−1=0．
解得 x1=2，x2=14．
10. 216∘
11. −2
12. −4,6
13. y=−8x
14. 0,7 或 73,0．
【解析】由题意，得
2−m=0，
解得 m=2，
3m+1=7，
点 P 的坐标是 0,7，
故答案是：0,7．
15. 110
16. 两，两点确定一条直线
第三部分
17. 原式 =0.25×4−1+3=3
18. （1） 3 对，△ACD∽△CBD，△ACD∽△ABC，△CBD∽△ABC．
∵∠ACB=90∘，CD⊥AB 于 D，
∴∠ACB=∠ADC=90∘，
又 ∵∠A 为公共角，
∴△ACD∽△ABC．
（2） 由（1）可知，△ACD∽△CBD，
∴AD:CD=CA:BC，
∴BC=CD×CA÷AD，
又 AD=3，CD=6，
在 Rt△ACD 中 AC2=AD2+CD2，AC=35，
∴BC=35×6÷3=65．
19. ∵x=2 是方程 x2−c=0 的一个根，
∴22−c=0，
∴c=4，
∴x2−4=0，
∴x2=4，
∴x=2 或 x=−2，
∴c 的值为 4，方程的另一根为 −2．
20. （1） y=400x．
（2） 方法一：
x≤400y≤80，
∴y≥5．
【解析】方法二：x=80，y=50，
∵x≤80，
∴y≥5．
21. （1） 补全的图形如图所示．
（2） 90∘；直径所对的圆周角是直角；过半径外端且垂直于这条半径的直线是圆的切线
22. （1） 由题意得 Δ=1+4c=0，
∴c=−14，
∴y=−x2+x−14，
∵ 当 x=−b2a=12 时，y=0，
∴ 顶点坐标为 12,0．
（2） ∵a=−1<0，开口向下，
∴ 当 x≥12 时，y 随 x 的增大而减小．
23. 如图所示，过 A 作 AE∥BC，则 ∠EAF=∠CBG=θ2，且 EC=AB=25 cm．
Rt△DAF 中，∠DAF=θ1，DF=AFtanθ1，Rt△EAF 中，∠EAF=θ2，EF=AFtanθ2，
∴DE=DF−EF=AFtanθ1−tanθ2．
∵AF=140 cm，tanθ1=1.082，tanθ2=0.412，
∴DE=140×1.082−0.412=93.8，
∴DC=DE+EC=93.8+25=118.8≈119 cm．
答：支架 DC 的高应为 119 cm．
24. （1） 设 y 关于 x 的函数解析式是 y=kx+bk≠0，由题图可得 b=6,15k+b=3, 解得 k=−15,b=6, 即 y 关于 x 的函数解析式是 y=−15x+6．
（2） 当 h=0 时，0=−310x+6，解得 x=20，
当 y=0 时，0=−15x+6，解得 x=30，
∵20<30，
∴ 甲先到达地面．
25. （1） 7.6．
（2） 描点，画图象．
（3） 1.5；2.6∼2.9（在范围内即可）
【解析】函数图象与直线 y=3x 交点的横坐标即为所求．
26. （1） ∵OA=OB，
∴∠OAB=∠B．
∵AC 为 ⊙O 切线，
∴OA⊥AC．
∴∠OAB+∠DAC=90∘．
∵OB⊥OC，
∴∠BOC=90∘．
∴∠ODB+∠B=90∘．
∴∠DAC=∠ODB．
∵∠ODB=∠CDA，
∴∠DAC=∠CDA．
∴AC=CD．
（2） ∵∠OAC=90∘，
∴OC=OA2+AC2=3．
∵CD=AC=2，
∴OD=OC−DC=3−2=1．
27. （1） 如图 1 所示，点 P 作 PF∥BC 交 AC 于点 F；
∵△ABC 是等边三角形，
∴△APF 也是等边三角形，
∴∠APF=∠BCA=60∘，AP=PF=AF=CQ，
∴∠FDP=∠DCQ，∠FDP=∠CDQ，
在 △PDF 和 △QDC 中，
∠PDF=∠QDC,∠DFP=∠QCD,PF=QC,
∴△PDF≌△QDCAAS，
∴PD=DQ；
（2） 如图 2 所示，过 P 作 PF∥BC 交 AC 于 F．
∵PF∥BC，△ABC 是等边三角形，
∴∠PFD=∠QCD，△APF 是等边三角形，
∴AP=PF=AF，
∵PE⊥AC，
∴AE=EF，
∵AP=PF，AP=CQ，
∴PF=CQ．
在 △PFD 和 △QCD 中，
∠PDF=∠QDC,∠DFP=∠QCD,PF=QC,
∴△PFD≌△QCDAAS，
∴FD=CD，
∵AE=EF，
∴EF+FD=AE+CD，
∴AE+CD=DE=12AC，
∵AC=6，
∴DE=3．
28. 过点 A 作 AD 垂直 x 轴于点 D．过点 B 作 BE⊥x 轴于点 E．
过点 C 作 CF⊥BE 于 F．过点 C 作 CQ⊥x 轴于点 G．
因为四边形 ABCO 为正方形，
所以 AO=OC，∠AOC=90∘．
所以 ∠AOD+∠COG=90∘．
因为 AD⊥x 轴，CG⊥x 轴，
所以 ∠ADO=∠CGO=90∘，
所以 ∠OAD+∠AOD=∠GCO+∠COB=90∘，
所以 ∠AOD=∠OCG，∠DAO=∠COG．
又因为 AO=CO，
所以 △AOD≌△OCG，
所以 AD=OG=3，OD=OG=1．
则 A 点坐标 −1,3．
因为 ∠BCF+∠FCO=90∘，∠FCO+∠OCG=90∘，
所以 ∠BCF=∠OCG，BC=OC，
所以 △BCF≌△OCG，
所以 CF=1，BF=3，
所以 BE=3+1，OE=OG−EG=OG−CF=3−1，
所以 B3−1,3+1．