2022届高考大一轮复习知识点精练：余弦函数的性质

这是一份2022届高考大一轮复习知识点精练：余弦函数的性质，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共20小题；共100分）
1. 要得到余弦曲线 y=csx，只需将正弦曲线 y=sinx 向左平移
A. π2 个单位B. π3 个单位C. π4 个单位D. π6 个单位

2. 设 α∈−π,π，且 csα=−12，则 α=
A. −2π3 或 2π3B. −π3 或 π3C. −π3 或 2π3D. −2π3 或 π3

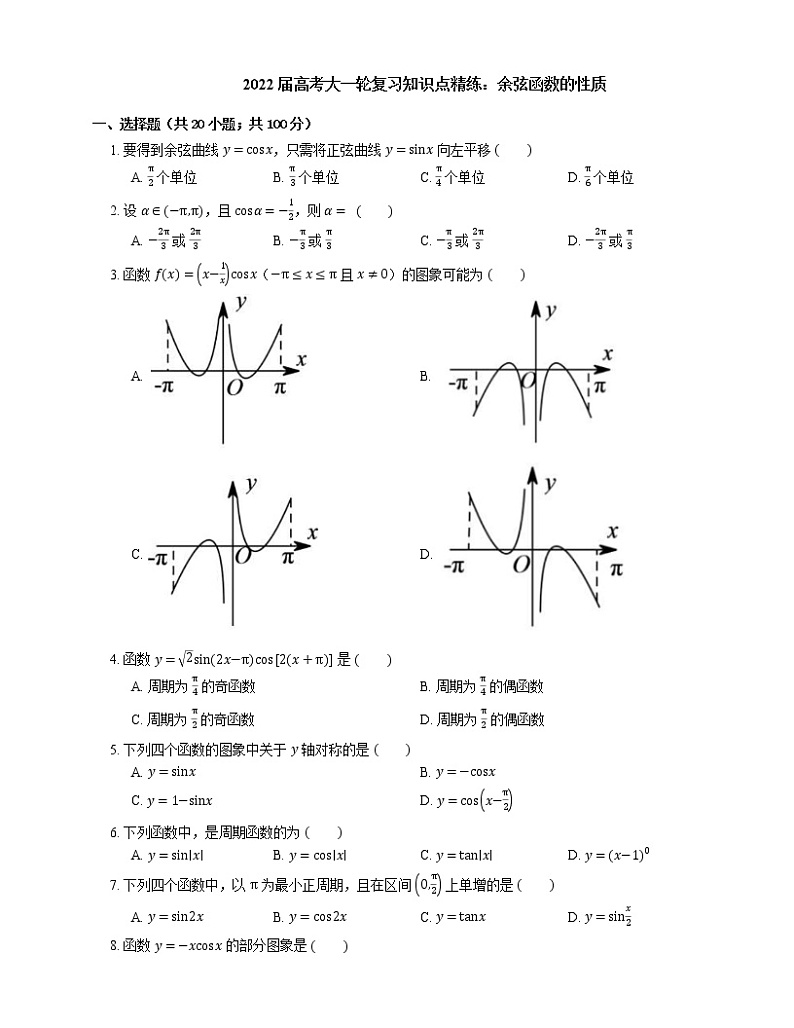
3. 函数 fx=x−1xcsx（−π≤x≤π 且 x≠0）的图象可能为
A. B.
C. D.

4. 函数 y=2sin2x−πcs2x+π 是
A. 周期为 π4 的奇函数B. 周期为 π4 的偶函数
C. 周期为 π2 的奇函数D. 周期为 π2 的偶函数

5. 下列四个函数的图象中关于 y 轴对称的是
A. y=sinxB. y=−csx
C. y=1−sinxD. y=csx−π2

6. 下列函数中，是周期函数的为
A. y=sin∣x∣B. y=cs∣x∣C. y=tan∣x∣D. y=x−10

7. 下列四个函数中，以 π 为最小正周期，且在区间 0,π2 上单增的是
A. y=sin2xB. y=cs2xC. y=tanxD. y=sinx2

8. 函数 y=−xcsx 的部分图象是
A. B.
C. D.

9. 函数 fx=sin2x+csx x∈0,π2 的最大值为
A. 1B. 54C. 32D. 2

10. y=∣csx∣ 的一个单调递增区间是
A. −π2,π2B. 0,πC. π,3π2D. 3π2,2π

11. 若 32sinx+12csx=4−m，则实数 m 的取值范围是
A. 3≤m≤5B. −5≤m≤5C. 3
12. 定义运算 a⊗b=a,a≤bb,a>b，例如，1⊗2=1，则函数 fx=sinx⊗csx 的值域为
A. 22,1B. −22,1C. −1,22D. −1,−22

13. 函数 y=cs2x 在下列哪个区间上是减函数
A. −π4,π4B. π4,3π4C. 0,π2D. π2,π

14. 函数 y=csx 的一个单调递增区间是
A. −π4,π4B. π4,34πC. π,32πD. 32π,2π

15. 在 △ABC 中，“A>B”是“cs2AA. 充分必要条件B. 充分非必要条件
C. 必要非充分条件D. 非充分非必要条件

16. 函数 fx=1−2sin22x 是
A. 偶函数且最小正周期为 π2B. 奇函数且最小正周期为 π2
C. 偶函数且最小正周期为 πD. 奇函数且最小正周期为 π

17. 我国著名数学家华罗庚先生曾说：数缺形时少直观，形缺数时难入微，数形结合百般好，隔离分家万事休．在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来琢磨函数图象的特征．函数 fx=2x+12x−1csx 的大致图象是
A. B.
C. D.

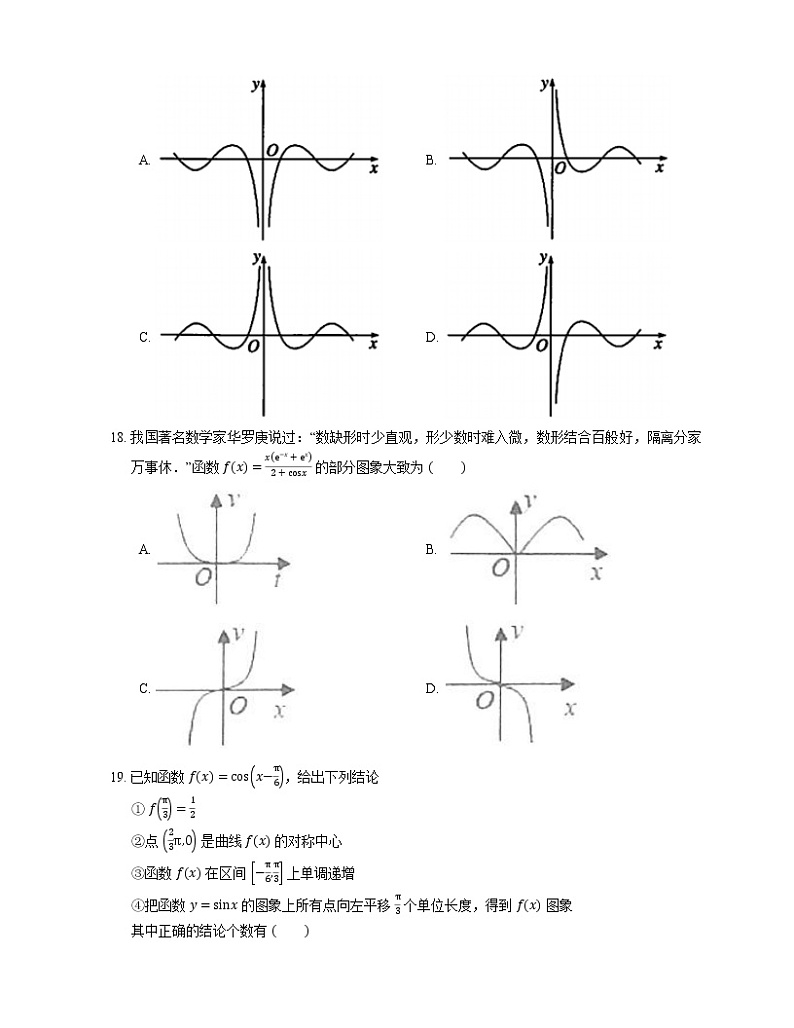
18. 我国著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休．”函数 fx=xe−x+ex2+csx 的部分图象大致为
A. B.
C. D.

19. 已知函数 fx=csx−π6，给出下列结论
① fπ3=12
②点 23π,0 是曲线 fx 的对称中心
③函数 fx 在区间 −π6,π3 上单调递增
④把函数 y=sinx 的图象上所有点向左平移 π3 个单位长度，得到 fx 图象
其中正确的结论个数有
A. 1 个B. 2 个C. 3 个D. 4 个

20. 函数 y=1−2csπ2x 的最小值，最大值分别是
A. −1，3B. −1，1C. 0，3D. 0，1

二、填空题（共5小题；共25分）
21. 当 x∈−2π,3π2 时，函数 y=csx 的单调递减区间为 ，最大值与最小值的和为 ．

22. 函数 fx=cs2x−sin2x 的最小正周期为 ．

23. 设常数 a∈R，若存在实数 m>−2π3，使得关于 x 的方程 csx=a 在区间 −2π3,m 内恰有一个解，则 a 的取值范围为 ．

24. 函数 fx=sin2x+3π2−3csx 的最小值为 ．

25. 设 α，β 都是锐角，csα=17，csα+β=5314．请问 csβ 是否可以求解，若能求解，求出答案；若不能求解，简述理由： ．

三、解答题（共6小题；共78分）
26. 求使 y=csx 取得最大值和最小值的 x 的集合．

27. 利用余弦线，研究余弦函数 y=csx 的单调性、最大值和最小值，并分别求出函数取得最大值和最小值时 x 的值．

28. 求函数 fx=−2sin2x+2csx 的最大值和最小值．

29. 已知对任意 x∈R，acsx+bcs2x≥−1 恒成立，求 a+bmax．

30. 已知函数 fx=sin2x+acsx−12 在 0≤x≤π2 上的最大值为 1，求实数 a 的值．

31. 已知函数 fx=csx−π≤x<0,sinx0≤x≤π.
（1）作出该函数的图象；
（2）若 fx=12，求 x 的值．
答案
第一部分
1. A
2. A【解析】因为 α∈−π,π，且 csα=−12，则 α=−2π3或2π3．
3. D【解析】函数 fx=x−1xcsx 可以看作是 gx=x−1x 与 hx=csx 两个函数的乘积，
其中 −π≤x≤π 且 x≠0．
分别研究函数 gx 与 hx 在各个区间的正负性，
可知函数 fx 的正负性符合D项．
4. C【解析】y=−2sin2xcs2x=−22sin4x，
因为 ω=4，
所以 T=2π4=π2，
又正弦函数为奇函数，
则函数为周期是 π2 的奇函数．
故选C．
5. B
【解析】设 fx=y=−csx，则 f−x=−cs−x=−csx=fx，
因为 y=−csx 是偶函数，其图象关于 y 轴对称，
故选B．
6. B【解析】因为 cs∣x∣=csx，
所以 y=cs∣x∣ 是周期函数．其余函数均不是周期函数．
7. C
8. D【解析】令 fx=−xcsx，
因为 f−x=xcs−x=x⋅csx=−fx，
所以函数 y=−xcsx 是奇函数，它的图象关于原点对称，
所以排除A，C，
当 x∈0,π2 时，y=−xcsx<0，排除B，于是选D．
9. B【解析】fx=sin2x+csx=−cs2x+csx+1=−csx−122+54，
因为 x∈0,π2，所以 csx∈0,1，所以 fxmax=54．
10. D
【解析】将 y=csx 的图象中位于 x 轴下方的部分关于 x 轴对称向上翻折，x 轴上方（或 x 轴上）的部分不变，即得 y=∣csx∣ 的图象（如图）．
11. A【解析】因为 32sinx+12csx=csxcsπ3+sinxsinπ3=csx−π3，
所以 csx−π3=4−m，于是 ∣4−m∣≤1，
解得 3≤m≤5．
12. C【解析】根据题设中的新定义，得 fx=sinx,sinx≤csxcsx,sinx>csx，
作出函数 fx 在一个周期内的图象（实线部分），
观察图象，可知函数 fx 的值域为 −1,22．
13. C【解析】函数 y=csx，x∈R 在 0,π 上是减函数，所以函数 y=cs2x 在 0,π2 上是减函数．
14. D
15. A
16. A【解析】fx=1−2sin22x=cs4x，f−x=cs−4x=cs4x=fx，
即 fx 是偶函数，T=2π4=π2．
17. B
18. C【解析】f−x=−xex+e−x2+cs−x=−fx，图象关于原点对称，B，
当 x>0 时，fx>7．
19. B
20. A
【解析】因为 x∈R，所以 π2x∈R，
所以 y=csπ2x 的值域为 −1,1．
所以 y=1−2csπ2x 的最大值为 3，最小值为 −1．
第二部分
21. −2π,−π，0,π，0
【解析】作出函数 y=csx，x∈−2π,3π2 的图象，如图所示．
观察图象可知函数 y=csx 的单调递减区间有两个：−2π,−π，0,π．
函数 y=csx 的最大值为 1，最小值为 −1．
所以最大值与最小值的和为 0．
22. π
【解析】因为 fx=cs2x，所以 fx 的最小正周期为 T=2π2=π．
23. −1,1
【解析】当 a<−1 或 a>1 时，方程总是无解．
当 −12≤a≤1 时，存在 m=0，方程 csx=a 在 −2π3,m 内恰有一个解，
当 −1≤a<−12 时，存在 m=π，方程 csx=a 在 −2π3,π 内恰有一个解．
所以 a 的取值范围为 −1,1．
24. −4
【解析】fx=sin2x+3π2−3csx=−cs2x−3csx=−2cs2x−3csx+1=−2csx+342+178.
因为 −1≤csx≤1，所以当 csx=1 时，
fxmin=−4，故函数 fx 的最小值是 −4．
25. α,α+β∈0,π，α<α+β，因为 y=csx 在 0,π 上单调递减，而 csα+β>csα．所以条件有误，不可解
第三部分
26. y=csx 取得最大值的 x 的集合为 xx=2kπ,k∈Z，
y=csx 取得最小值的 x 的集合为 xx=2k+1π,k∈Z．
27. 余弦函数 y=csx 的单调递增区间是 −π+2kπ,2kπ（k∈Z），单调递减区间是 2kπ,π+2kπ（k∈Z）．当 x=2kπ（k∈Z）时，函数 y=csx 取得最大值 1；当 x=π+2kπ（k∈Z）时，函数 y=csx 取得最小值 −1．
28. fx=−2sin2x+2csx=2cs2x+2csx−2=2csx+122−52.
因为 −1≤csx≤1，
所以当 csx=1 时，fxmax=2；
当 csx=−12 时，fxmin=−52．
29. 解法一：原不等式即 b2cs2x−1+acsx+1≥0，即 2bcs2x+acsx−b+1≥0．
令 ft=2bt2+at−b+1，其中 t=csx∈−1,1．
（1）b≤0,f−1=2b−a−b+1≥0,f1=2b+a−b+1≥0⇒a+b≤2b+1≤1<2，
（2）b>0,−a4b∉−1,1,b−a+1≥0,b+a+1≥0⇒a<−4b 或 a>4b．
若 a<−4b，则 a+b<−3b<0<2；或 a>4b，则由 b−a+1≥0，得 4b（3）b>0,−a4b∈−1,1,a2≤8b1−b⇒a2+8b2−8b≤0，即 a2+8b−122≤2．
由柯西不等式有 2×98≥a2+8b−1221+18≥a+b−122，
故 a+b−12≤32，即 a+b≤2．当且仅当 a=43，b=23 时等号成立，此时满足 −a4b=−12∈−1,1．
综上所述，a+bmax=2．
解法二：在 acsx+bcs2x≥−1 中取 x=23π，得 a⋅−12+b⋅−12≥−1，
所以 a+b≤2，且当 a=43，b=23 时，
acsx+bcs2x=43csx+23cs2x=43csx+232cs2x−1=43csx+122−1≥−1,
所以 a+bmax=2．
30. 设 csx=t，则 fx=−t−a22+a24+12，
分别对 0≤a≤2，a<0，a>2 进行讨论，可得 a=2．
31. （1） 作出函数 fx=csx−π≤x<0,sinx0≤x≤π. 的图象，如图①所示．
（2） 因为 fx=12，所以在图①基础上再作直线 y=12，如图②所示，
则当 −π≤x<0 时，由图象知 x=−π3，
当 0≤x≤π 时，x=π6 或 x=5π6．
综上，可知 x 的值为 −π3 或 π6 或 5π6．