2021年北京昌平区昌平二一学校八年级下期末数学试卷

这是一份2021年北京昌平区昌平二一学校八年级下期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 在平面直角坐标系中，点 A−2,3 在
A. 第一象限B. 第二象限C. 第三象限D. 第四象限

2. 某校进行参加区级数学学科竞赛选手选拔，经过多次测试后，有四位同学成为晋级的候选人，具体情况如下表，如果从这四位同学中选出一名晋级，你会推荐
甲乙丙丁平均分92949492方差35352323
A. 甲B. 乙C. 丙D. 丁

3. 用配方法解方程 x2+4x+1=0 时，原方程应变形为
A. x+22=3B. x−22=3C. x+22=5D. x−22=5

4. 一个寻宝游戏的寻宝通道由正方形 ABCD 的边组成，如图 1 所示．为记录寻宝者的行进路线，在 AB 的中点 M 处放置了一台定位仪器，设寻宝者行进的时间为 x，寻宝者与定位仪器之间的距离为 y，若寻宝者匀速行进，且表示 y 与 x 的函数关系的图象大致如图 2 所示，则寻宝者的行进路线可能为
A. A→BB. B→CC. C→DD. D→A

5. 如图，点 A 与点 B 关于点 O 中心对称，则下列说法错误的是
A. O 为 AB 中点
B. 点 A，B，O 共线
C. 点 A 绕 O 旋转 90∘ 与点 B 重合
D. 点 A 绕 O 旋转 180∘ 与点 B 重合

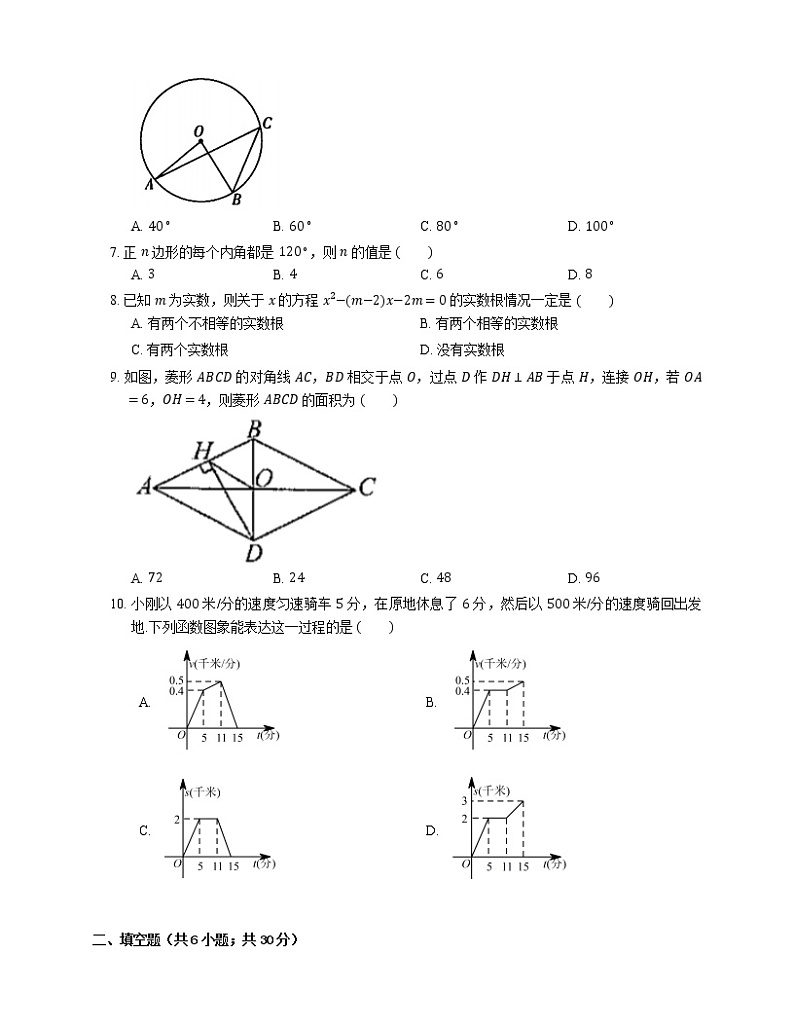
6. 如图，A，B，C 三点在 ⊙O 上，∠AOB=80∘，则 ∠ACB 的度数为
A. 40∘B. 60∘C. 80∘D. 100∘

7. 正 n 边形的每个内角都是 120∘，则 n 的值是
A. 3B. 4C. 6D. 8

8. 已知 m 为实数，则关于 x 的方程 x2−m−2x−2m=0 的实数根情况一定是
A. 有两个不相等的实数根B. 有两个相等的实数根
C. 有两个实数根D. 没有实数根

9. 如图，菱形 ABCD 的对角线 AC，BD 相交于点 O，过点 D 作 DH⊥AB 于点 H，连接 OH，若 OA=6，OH=4，则菱形 ABCD 的面积为
A. 72B. 24C. 48D. 96

10. 小刚以 400 米/分的速度匀速骑车 5 分，在原地休息了 6 分，然后以 500 米/分的速度骑回出发地.下列函数图象能表达这一过程的是
A. B.
C. D.

二、填空题（共6小题；共30分）
11. 如图，在 △ABC 中，AB=AD=DC，∠BAD=20∘，则 ∠C= ．

12. 已知 P1−3,y1，P22,y2 是一次函数 y=2x+1 的图象上的两个点，则 y1，y2 的大小关系是 ．

13. 已知菱形的两条对角线长为 8 cm 和 6 cm，这个菱形的面积是 cm2．

14. 课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边用周长为 30 米的篱笆围成．已知墙长为 18 米，围成苗圃园的面积为 72 平方米，设这个苗圃园垂直于墙的一边长为 x 米．可列方程为 ．

15. 阅读下面材料：
在数学课上，老师提出如下问题：
已知：如图，四边形 ABCD 是平行四边形．
求作：菱形 AECF，使点 E，F 分别在 BC，AD 上．
小凯的作法如下：
（1）连接 AC；
（2）作 AC 的垂直平分线 EF 分别交 BC，AD 于 E，F；
（3）连接 AE，CF．
所以四边形 AECF 是菱形．
老师说：“小凯的作法正确．”
请回答：在小凯的作法中，判定四边形 AECF 是菱形的依据是 ．

16. 函数 y=x−2 中，自变量 x 的取值范围是 ．

三、解答题（共12小题；共156分）
17. 解方程：x−52−9=0．

18. 如图，在平行四边形 ABCD 中，E，F 是对角线 BD 上的两点且 BE=DF，连接 AE，CF．求证：AE=CF．

19. 已知直线 y=−x+4．
（1）直接写出直线与 x 轴、 y 轴的交点 A，B 的坐标；
（2）画出图象；
（3）求直线与坐标轴围成的三角形的面积．

20. 一次函数 y1=kx+3 与正比例函数 y2=−2x 交于点 A−1,2．
（1）确定一次函数表达式；
（2）当 x 取何值时，y1<0?
（3）当 x 取何值时，y1>y2?

21. 某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系．每盆植入 3 株时，平均单株盈利 3 元；以同样的栽培条件，若每盆每增加 1 株，平均单株盈利就减少 0.5 元．要使每盆盈利 10 元，每盆应该植多少株?

22. 如图，在四边形 ABCD 中，∠ABC=90∘，AC=AD，M，N 分别为 AC，CD 的中点，连接 BM，MN，BN．
（1）求证：BM=MN；
（2）若 ∠BAD=60∘，AC 平分 ∠BAD，AC=2，写出求 BN 长的思路．

23. 阅读材料，解决问题：
明明家准备装修房子，房子的部分平面图如图 1 所示．为了增大房子的使用空间，爸爸想把现在两间卧室之间的非承重墙打掉，之后在打掉的位置做一排衣柜．
爸爸说：“我想测量一下非承重墙的厚度，从而知道打掉这堵墙后可以腾出多少空间．我手里有的工具是教学用量角器、大刻度尺，明明，你帮助爸爸看看应该怎样测量．”
“这堵墙的厚度处处相等吗?”明明说．
爸爸说：“这个没问题，当年收房的时候我就考察过．”
“那我就可以在地面上直接进行测量了．我再问您，每个房间中地面和墙的交线都是垂直或平行的吗?”明明说．
爸爸回答：“是的”．
“那就简单了．我们俩先测出客厅的东西向宽度，再测出每个卧室的东西向宽度，用客厅的宽度减去两个卧室的宽度就是中间这堵非承重墙的厚度．”明明说．
爸爸说：“那不行，客厅和卧室的家具摆得满满的，东西向宽度勉强测到也不准确．你能不能在不借助测量房间宽度或房间内其它家具的前提下，设计一个通过测量和计算得到非承重墙厚度的方案．”
请你利用学到的三角形或四边形的知识帮助明明解决此问题．
要求：（1）在图 2 中画出测量时用到的示意图，图形要规范；
（2）简要叙述测量过程；
（3）写出测量的依据．

24. 在平面直角坐标系中，直线 y=−x+2 与 y 轴交于点 A，点 A 关于 x 轴的对称点为 B，过点 B 作 y 轴的垂线 l，直线 l 与直线 y=−x+2 交于点 C．
（1）求点 B，C 的坐标；
（2）若直线 y=2x+b 与 △ABC 有两个公共点，直接写出 b 的取值范围．

25. 解方程：x2−4x+1=0．

26. 已知关于 x 的方程 x2+3x+3m4=0 有两个不相等的实数根．
（1）求 m 的取值范围；
（2）若 m 为符合条件的最大整数，求此时方程的根．

27. 为了解某地区中学生一周课外阅读时长的情况，随机抽取部分中学生进行调查，根据调查结果，将阅读时长分为四类：2 小时以内，2∼4 小时（含 2 小时），4∼6 小时（含 4 小时），6 小时及以上，并绘制了如图所示尚不完整的统计图．
（1）本次调查共随机抽取了 名中学生，其中课外阅读时长“2∼4 小时”的有 人．
（2）扇形统计图中，课外阅读时长“4∼6 小时”对应的圆心角度数为 ∘．
（3）若该地区共有 20000 名中学生，估计该地区中学生一周课外阅读时长不少于 4 小时的人数．

28. 数学活动课上，张老师引导同学进行如下探究：
如图 1，将长为 12 cm 的铅笔 AB 斜靠在垂直于水平桌面 AE 的直尺 FO 的边沿上，一端 A 固定在桌面上，图 2 是示意图．
活动一
如图 3，将铅笔 AB 绕端点 A 顺时针旋转，AB 与 OF 交于点 D，当旋转至水平位置时，铅笔 AB 的中点 C 与点 O 重合．
数学思考
（1）设 CD=x cm，点 B 到 OF 的距离 GB=y cm．
①用含 x 的代数式表示：AD 的长是 cm，BD 的长是 cm；
② y 与 x 的函数关系式是 ，自变量 x 的取值范围是 ．
（2）活动二
①列表：根据（1）中所求函数关系式计算并补全表格．

②描点：根据表中数值，继续描出①中剩余的两个点 x,y．
③连线：在平面直角坐标系中，请用平滑的曲线画出该函数的图象．
（3）数学思考
请你结合函数的图象，写出该函数的两条性质或结论．
答案
第一部分
1. B
2. C
3. A
4. A【解析】观察图 2 得寻宝者与定位仪之间的距离先越来越近，到达 M 后再越来越远，结合图 1，寻宝者的行进路线为 A 到 B．
5. C
6. A【解析】∵∠ABO=80∘，
∴∠ACB=12∠AOB=12×80∘=40∘．
7. C
8. C【解析】Δ=m−22−4×−2m=m+22．
对于任意实数 m，都有 m+22≥0，即 Δ≥0，
所以原方程一定有两个实数根．
9. C
10. C
第二部分
11. 40∘
【解析】∵AB=AD，∠BAD=20∘，
∴∠B=12180∘−∠BAD=12180∘−20∘=80∘．
∵∠ADC 是 △ABD 的外角，
∴∠ADC=∠B+∠BAD=80∘+20∘=100∘．
∵AD=DC．
∴∠C=12180∘−∠ADC=12180∘−100∘=40∘．
12. y113. 24
14. x30−2x=72 或 x2−15x+36=0
15. 对角线互相平分且垂直的四边形是菱形
16. x≥2
【解析】依题意，得 x−2≥0，解得：x≥2．
第三部分
17.
x−52=9.
得
x−5=±3.
即
x−5=3或x−5=−3.
解得
x1=8,x2=2.
18. 连接 AF，CE，连接 AC 交 BD 于点 O．如图，
因为四边形 ABCD 是平行四边形，
所以 OA=OC，OB=OD，
又因为 BE=DF，
所以 OE=OF，
所以四边形 AECF 是平行四边形，
所以 AE=CF．
19. （1） A4,0，B0,4．
（2） 如图．
（3） ∵A4,0，B0,4，
∴OA=4，OB=4，
∴S△AOB=12⋅OA⋅OB=12×4×4=8．
∴ 直线与坐标轴围成的三角形的面积为 8．
20. （1） 由已知，将点 A−1,2 代入 y1=kx+3 得 2=−k+3，
解得：k=1．
所以一次函数表达式为：y1=x+3．
（2） 由（1）得一次函数表达式为 y1=x+3，
令 y1<0，得 x+3<0，
解得 x<−3．
所以，当 x<−3 时，y1<0．
方法不唯一．
（3） 因为 y1>y2，
所以 x+3>−2x，
计算得出：x>−1，
当 x>−1 时，y1>y2．
方法不唯一．
21. 设每盆花苗增加 x 株，则每盆花苗有 x+3 株，平均单株盈利为 3−0.5x 元，
由题意，得
x+33−0.5x=10.
化简，整理，得
x2−3x+2=0.
解这个方程，得
x1=1,x2=2.
则 3+1=4，3+2=5，
答：要使得每盆盈利 10 元，每盆应该植入 4 株或 5 株．
22. （1） ∵∠ABC=90∘，M 为 AC 中点，
∴ BM=12AC，
∵ M 为 AC 中点，N 为 DC 中点，
∴ MN=12AD，
∵ AD=AC，
∴ BM=MN．
（2） 由已知可证 ∠DAC=∠CAB=30∘，BM=AM=12AC=1，
根据三角形外角性质可证 ∠CMB=60∘，
根据三角形中位线定理可证 MN∥AD，MN=12AD=1，∠DAC=∠NMC=30∘，
可得三角形 NMB 是直角三角形，
根据三角形勾股定理可得出 BN 的长 =BM2+MN2=2．
23. 答案不唯一．
如图，
在椭圆垛的两边测出 AC=BD，过点 C，D 作出 CE⊥AC，DF⊥BD 可知 E，C，D，F 在一条直线上，同时测出 EC，DF 的长，在客厅内找一点 P，连接 PE，PF，通过测量找得 PE，PF 的中点 M，N，测出 MN 的长，
根据三角形的中位线定理即可得 EF 的长，用 EF 的长减去 EC，DF 的长即可得 CD 的长．
24. （1） 在 y=−x+2 中，令 x=0 得 y=2，
所以 A0,2，
由此得出点 A 关于 x 轴对称点为 B0,−2，
把 y=−2 代入 y=−x+2 中得 x=4，
所以 C4,−2．
（2） −1025. 方法一：
移项得：
x2−4x=−1,
配方得：
x2−4x+4=−1+4,
即：
x−22=3,
开方得：
x−2=±3,
所以原方程的解是：
x1=2+3,x2=2−3.
【解析】方法二：
x2−4x+1=0．
因为 a=1，b=−4，c=1，
所以 b2−4ac=−42−4×1×1=12．
所以
x=−b±b2−4ac2a=4±122=4±232=2±3.
所以原方程的解是 x1=2+3，x2=2−3．
26. （1） ∵ 关于 x 的方程 x2+3x+3m4=0 有两个不相等的实数根，
∴Δ=9−3m>0．
∴m<3．
（2） ∵m 为符合条件的最大整数，
∴m=2．
此时整理方程，得
x2+3x+32=0.
配方，得
x2+3x+322=−32+322,
x+322=34.
由此可得
x1=3−32,x2=−3−32.
27. （1） 200；40
【解析】本次调查共随机抽取了：50÷25%=200（名）中学生，
其中课外阅读时长“2∼4 小时”的有：200×20%=40（人），
故答案为：200；40．
（2） 144
【解析】扇形统计图中，课外阅读时长“4∼6 小时”对应的圆心角度数为：360∘×1−30200−20%−25%=144∘，
故答案为：144．
（3） 20000×1−30200−20%=13000（人），
答：该地区中学生一周课外阅读时长不少于 4 小时的有 13000 人．
28. （1） 6+x；6−x；y=36−6x6+x；0≤x≤6
【解析】①如图中，由题意 AC=OA=12AB=6 cm，
∵ CD=x cm，
∴ AD=6+x cm，BD=12−6+x=6−x cm．
②作 BG⊥OF 于 G．
∵ OA⊥OF，BG⊥OF，
∴ BG∥OA，
∴ BGOA=BDAD，
∴ y6=6−x6+x，
∴ y=36−6x6+x 0≤x≤6．
（2） ①当 x=3 时，y=2，当 x=0 时，y=6．
②点 0,6，点 3,2 如图所示．
③函数图象如图所示．
（3） 性质 1：函数值 y 的取值范围为 0≤y≤6．
性质 2：函数图象在第一象限，y 随 x 的增大而减小．