2021年北京朝阳区北京中央美术实验学校八年级下期末数学试卷
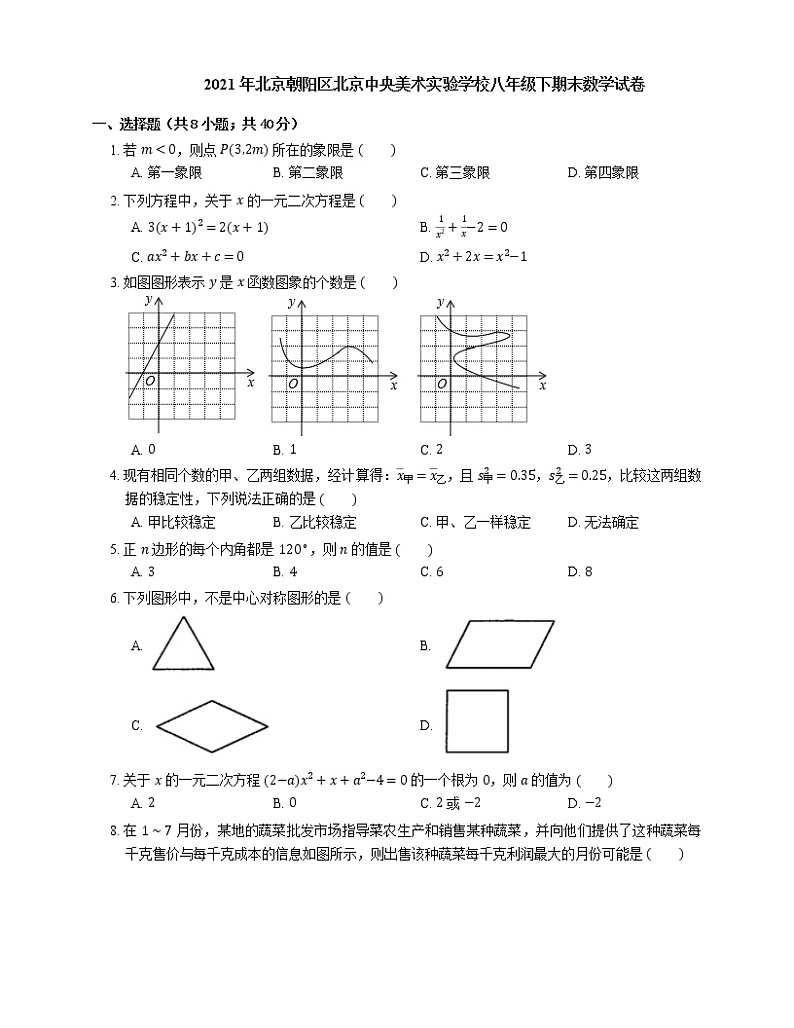
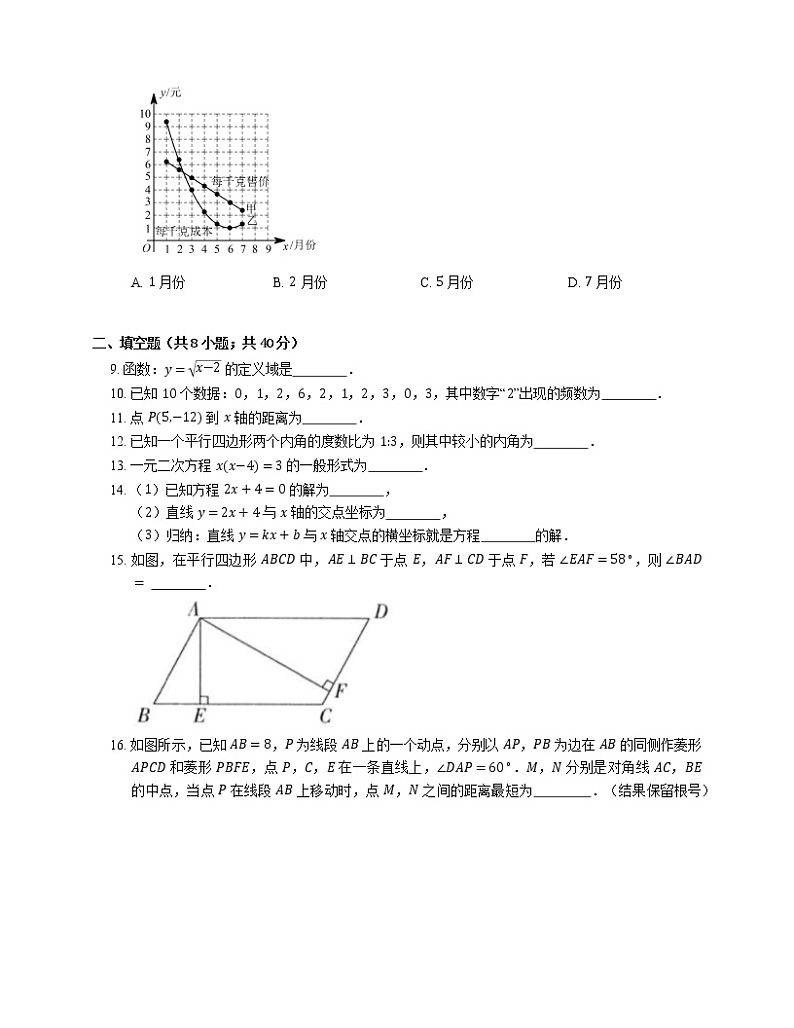
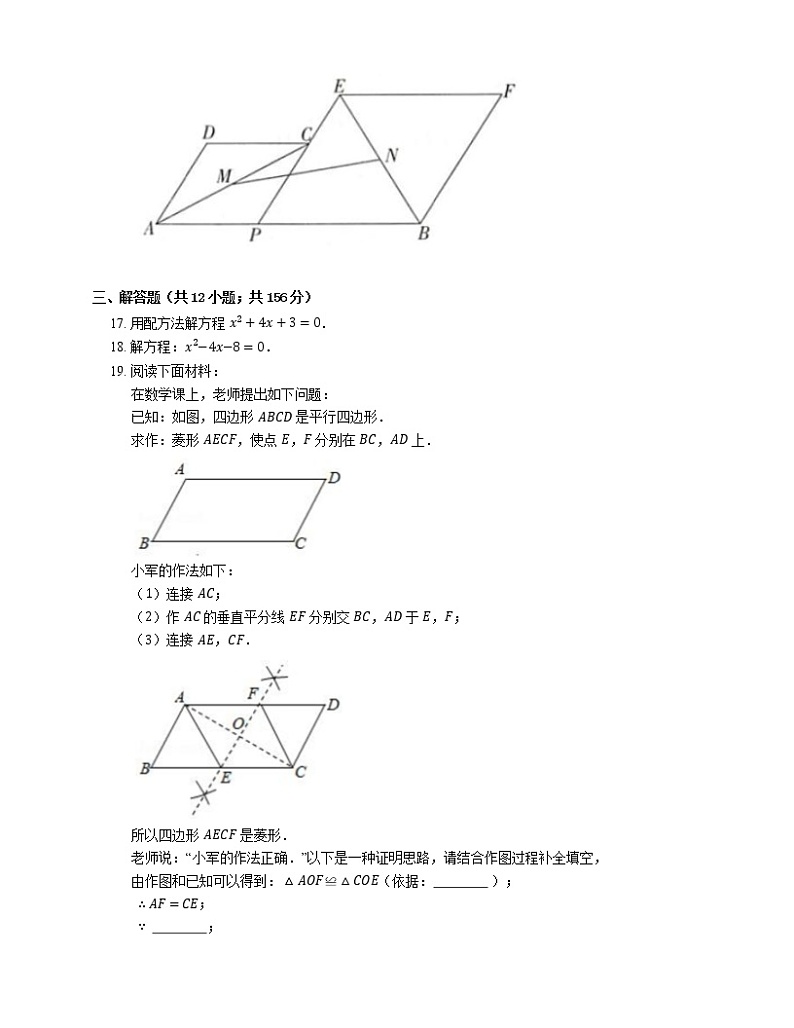
展开2021年北京朝阳区北京中央美术实验学校八年级下期末数学试卷 一、选择题(共8小题;共40分)1. 若 m<0,则点 P3,2m 所在的象限是 A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 2. 下列方程中,关于 x 的一元二次方程是 A. 3x+12=2x+1 B. 1x2+1x−2=0 C. ax2+bx+c=0 D. x2+2x=x2−1 3. 如图图形表示 y 是 x 函数图象的个数是 A. 0 B. 1 C. 2 D. 3 4. 现有相同个数的甲、乙两组数据,经计算得:x甲=x乙,且 s甲2=0.35,s乙2=0.25,比较这两组数据的稳定性,下列说法正确的是 A. 甲比较稳定 B. 乙比较稳定 C. 甲、乙一样稳定 D. 无法确定 5. 正 n 边形的每个内角都是 120∘,则 n 的值是 A. 3 B. 4 C. 6 D. 8 6. 下列图形中,不是中心对称图形的是 A. B. C. D. 7. 关于 x 的一元二次方程 2−ax2+x+a2−4=0 的一个根为 0,则 a 的值为 A. 2 B. 0 C. 2 或 −2 D. −2 8. 在 1∼7 月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是 A. 1 月份 B. 2 月份 C. 5 月份 D. 7 月份 二、填空题(共8小题;共40分)9. 函数:y=x−2 的定义域是 . 10. 已知 10 个数据:0,1,2,6,2,1,2,3,0,3,其中数字“2”出现的频数为 . 11. 点 P5,−12 到 x 轴的距离为 . 12. 已知一个平行四边形两个内角的度数比为 1:3,则其中较小的内角为 . 13. 一元二次方程 xx−4=3 的一般形式为 . 14. (1)已知方程 2x+4=0 的解为 , (2)直线 y=2x+4 与 x 轴的交点坐标为 , (3)归纳:直线 y=kx+b 与 x 轴交点的横坐标就是方程 的解. 15. 如图,在平行四边形 ABCD 中,AE⊥BC 于点 E,AF⊥CD 于点 F,若 ∠EAF=58∘,则 ∠BAD= . 16. 如图所示,已知 AB=8,P 为线段 AB 上的一个动点,分别以 AP,PB 为边在 AB 的同侧作菱形 APCD 和菱形 PBFE,点 P,C,E 在一条直线上,∠DAP=60∘.M,N 分别是对角线 AC,BE 的中点,当点 P 在线段 AB 上移动时,点 M,N 之间的距离最短为 .(结果保留根号) 三、解答题(共12小题;共156分)17. 用配方法解方程 x2+4x+3=0. 18. 解方程:x2−4x−8=0. 19. 阅读下面材料: 在数学课上,老师提出如下问题: 已知:如图,四边形 ABCD 是平行四边形. 求作:菱形 AECF,使点 E,F 分别在 BC,AD 上. 小军的作法如下: (1)连接 AC; (2)作 AC 的垂直平分线 EF 分别交 BC,AD 于 E,F; (3)连接 AE,CF. 所以四边形 AECF 是菱形. 老师说:“小军的作法正确.”以下是一种证明思路,请结合作图过程补全填空, 由作图和已知可以得到:△AOF≌△COE(依据: ); ∴AF=CE; ∵ ; ∴ 四边形 AECF 是平行四边形(依据: ); ∵EF 垂直平分 AC; ∴ (依据: ); ∴ 四边形 AECF 是菱形. 20. 对某一个函数给出如下定义:若存在实数 M>0,对于任意的函数值 y,都满足 −M≤y≤M,则称这个函数是有界函数,在所有满足条件的 M 中,其最小值称为这个函数的边界值,例如,图中的函数,它的最大值是 12,最小值是 −1,它也是有界函数,其边界值是 1. (1)分别判断函数 y=1x1≤x≤5 和 y=x+1x>0 是不是有界函数,若是有界函数,求其边界值;(2)若函数 y=−2x−1a≤x≤b,aBC,BC=9 厘米.P,Q 分别从 A,C 同时出发,P 以 1 厘米/秒的速度由 A 向 D 运动.Q 以 2 厘米/秒的速度由 C 向 B 运动,问几秒时,四边形 ABQP 是平行四边形? 22. 如图,直线 l1:y=2x+1 与直线 l2:y=mx+4 相交于点 P1,b. (1)求 b,m 的值;(2)垂直于 x 轴的直线 x=a 与直线 l1,l2 分别交于点 C,D,若线段 CD 的长为 2,求 a 的值. 23. 如图,将矩形 ABCD 沿对角线 BD 对折,顶点 C 落在点 E 上,若 BC=10,AB=5. (1)求证:△ABO≌△EDO;(2)求 AO 的长. 24. 某百货商场经理对新进某一品牌几种号码的男式跑步鞋的销售情况进行了一周的统计,得到一组数据后,绘制了频数(双)频率统计表与频数分布直方图如下: 一周销售数量统计表 号码频数/双频率39100.140150.1541a0.342bc43150.154450.05 请你根据图表中提供的信息,解答以下问题:(1)写出表中 a,b,c 的值;(2)补全频数分布直方图;(3)根据市场实际情况,该商场计划再进 1000 双这种跑步鞋,请你帮助商场经理估计一下需要进多少双 41 号的跑步鞋? 25. 如图 1,已知正方形 ABCD 的对角线 AC,BD 相交于点 O,E 是 AC 上一点,连接 EB,过点 A 作 AM⊥BE,垂足为 M,AM 交 BD 于点 F. (1)试说明 OE=OF;(2)如图 2,若点 E 在 AC 的延长线上,AM⊥BE 交 EB 的延长线于点 M,交 DB 的延长线于点 F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出说明理由;如果不成立,请说明理由. 26. 如图,抛物线 y=−x2+4x+m−4(m 为常数)与 y 轴交点为 C,M3,0,N0,−2 分别是 x 轴、 y 轴上的点. (1)求点 C 的坐标(用含 m 的代数式表示);(2)若抛物线与 x 轴有两个交点 A,B,是否存在这样的 m,使得线段 AB=MN,若存在,求出 m 的值,若不存在,请说明理由;(3)若抛物线与线段 MN 有公共点,求 m 的取值范围. 27. 在平面直角坐标系 xOy 中,对于点 Px,y,若点 Q 的坐标为 ax+y,x+ay,其中 a 为常数,则称点 Q 是点 P 的“a 级关联点”.例如,点 P1,4 的“3 级关联点”为 Q3×1+4,1+3×4,即 Q7,13. (1)已知点 A−2,6 的“12 级关联点”是点 A1,点 B1,b 的“2 级关联点”是点 B13,3,求点 A1 和点 B 的坐标.(2)已知点 Mm−1,2m 的“−3 级关联点”Mʹ 位于 y 轴上,求 Mʹ 的坐标.(3)已知点 C−1,3,D4,3,点 N1,y 和它的“4 级关联点”Nʹ 到 CD 所在直线的距离相等.求点 N 及 Nʹ 的坐标. 28. 在平面直角坐标系 xOy 中,对于 Pa,b 和 Qa,bʹ 给出如下定义: 如果 bʹ=b,a≥1−b,a<1,那么点 Q 就是点 P 的关联点. 例如,点 2,4 的关联点是 2,4,点 −1,4 的关联点是 −1,−4. (1)点 2,1 的关联点是 ,点 −5,1 的关联点是 .(2)如果点 A−1,−2 和点 B−1,2 中有一个点是直线 y=2x 上某一点的关联点,那么这个点是 .(3)如果点 P 在直线 y=−x+3−2≤x≤k,k>−2 上,其关联点 Q 的纵坐标 bʹ 的取值范围是 −5≤bʹ≤2,求 k 的取值范围.答案第一部分1. D 【解析】∵m<0, ∴2m<0, ∴ 点 P3,2m 在第四象限.2. A 3. C 【解析】第一个图象,对每一个 x 的值,都有唯一确定的 y 值与之对应,是函数图象;第二个图象,对每一个 x 的值,都有唯一确定的 y 值与之对应,是函数图象;第三个图象,对给定的 x 的值,有两个 y 值与之对应,不是函数图象;综上所述,表示 y 是 x 的函数的有第一个、第二个,共 2 个.4. B 5. C 6. A 【解析】选项B,C,D中的图形都是中心对称图形,选项A中的图形是轴对称图形,而不是中心对称图形.7. D 【解析】∵2−ax2+x+a2−4=0 是关于 x 的一元二次方程,一个根是 0, ∴2−a≠0,a2−4=0, ∴a=−2.8. C 第二部分9. x≥2【解析】根据题意得:x−2≥0,解得:x≥2.10. 3【解析】已知 10 个数据:0,1,2,6,2,1,2,3,0,3,其中数字“2”出现了 3 次,故数字“2”出现的频数为:3.11. 12【解析】因为点 P 的坐标为 5,−12,所以点 P 到 x 轴的距离为 −12=12.故答案为:12.12. 45∘13. x2−4x−3=014. x=−2,−2,0,kx+b=015. 122∘【解析】因为 AE⊥BC 于点 E,AF⊥CD 于点 F,所以 ∠AEC=∠AFC=90∘,又因为 ∠EAF=58∘,所以 ∠C=360∘−58∘−90∘−90∘=122∘,因为四边形 ABCD 是平行四边形,所以 ∠BAD=∠C=122∘.16. 23【解析】如图,连接 PM,PN. ∵ 四边形 APCD,四边形 PBFE 都是菱形,∠DAP=60∘, ∴∠APC=120∘,∠EPB=60∘,∠PAC=30∘, ∵M,N 分别是对角线 AC,BE 的中点, ∴∠CPM=12∠APC=60∘,∠EPN=12∠EPB=30∘,PM⊥AC,PN⊥BE, ∴∠MPN=60∘+30∘=90∘,设 PA=2a,则 PB=8−2a, ∴PM=a,PN=34−a, ∴MN=a2+34−a2=4a−32+12. ∴ 当 a=3 时,MN 有最小值,最小值为 23.第三部分17. x2+4x=−3,x2+4x+22=−3+22,x+22=1,x+2=±1,x=−2±1,所以x1=−1,x2=−3.18. a=1,b=−4,c=−8, Δ=16−4×1×−8=48, x=4±482, x1=2+23,x2=2−23.19. ASA;AF∥CE;一组对边平行且相等的四边形是平行四边形;AF=FC;垂直平分线的上的点到线段两个端点的距离相等【解析】根据作图过程可知:△AOF≌△COEASA; ∴AF=CE; ∵AF∥CE; ∴ 四边形 AECF 是平行四边形(一组对边平行且相等的四边形是平行四边形); ∵EF 垂直平分 AC; ∴AF=FC(垂直平分线的上的点到线段两个端点的距离相等); ∴ 四边形 AECF 是菱形.20. (1) 函数 y=1x1≤x≤5 是有界函数,函数 y=x+1x>0 不是有界函数.对于函数 y=1x1≤x≤5 有 15≤y≤1, ∴ 其边界值为 1. (2) ∵ 函数 y=−2x−1a≤x≤b 中 y 随 x 的增大而减小, ∴ 当 x=a 时,y最大值=3,即 −2a−1=3,解得 a=−2.当 x=b 时,y最小值=−2b−1. ∵ 边界值是 3, ∴3≤−2b−1≤3, ∴−2≤b≤1, ∵b>a,且 a=−2, ∴−2
2021年北京朝阳区樱花园实验学校中学部八年级下期末数学试卷: 这是一份2021年北京朝阳区樱花园实验学校中学部八年级下期末数学试卷,共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021年北京朝阳区中国科学院附属实验学校分校八年级下期末数学试卷: 这是一份2021年北京朝阳区中国科学院附属实验学校分校八年级下期末数学试卷,共11页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021年北京朝阳区北京中学八年级下期末数学试卷: 这是一份2021年北京朝阳区北京中学八年级下期末数学试卷,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












