2021年北京大兴区大兴区兴海学校八年级上期末数学试卷

这是一份2021年北京大兴区大兴区兴海学校八年级上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 三角形中，到三边距离相等的点是
A. 三条高线的交点B. 三条中线的交点
C. 三条角平分线的交点D. 三边垂直平分线的交点

2. 下列图形中，不是轴对称图形的是
A. B.
C. D.

3. 斑叶兰被列为国家二级保护植物，它的一粒种子重约 0.0000005 克．将 0.0000005 用科学记数法表示为
A. 5×107B. 5×10−7C. 0.5×10−6D. 5×10−6

4. 使代数式 1x+3+4−3x 有意义的整数 x 有
A. 5 个B. 4 个C. 3 个D. 2 个

5. 若三角形的三边长分别是 a，b，c，且 a−252+a−b−1+∣c−4∣=0，则这个三角形的周长是
A. 25+5B. 45−3C. 45+5D. 45+3

6. 如图，若 △ABC≌△ADE，则选项结论中一定成立的是
A. AC=DEB. ∠BAD=∠CAE
C. AB=AED. ∠ABC=∠AED

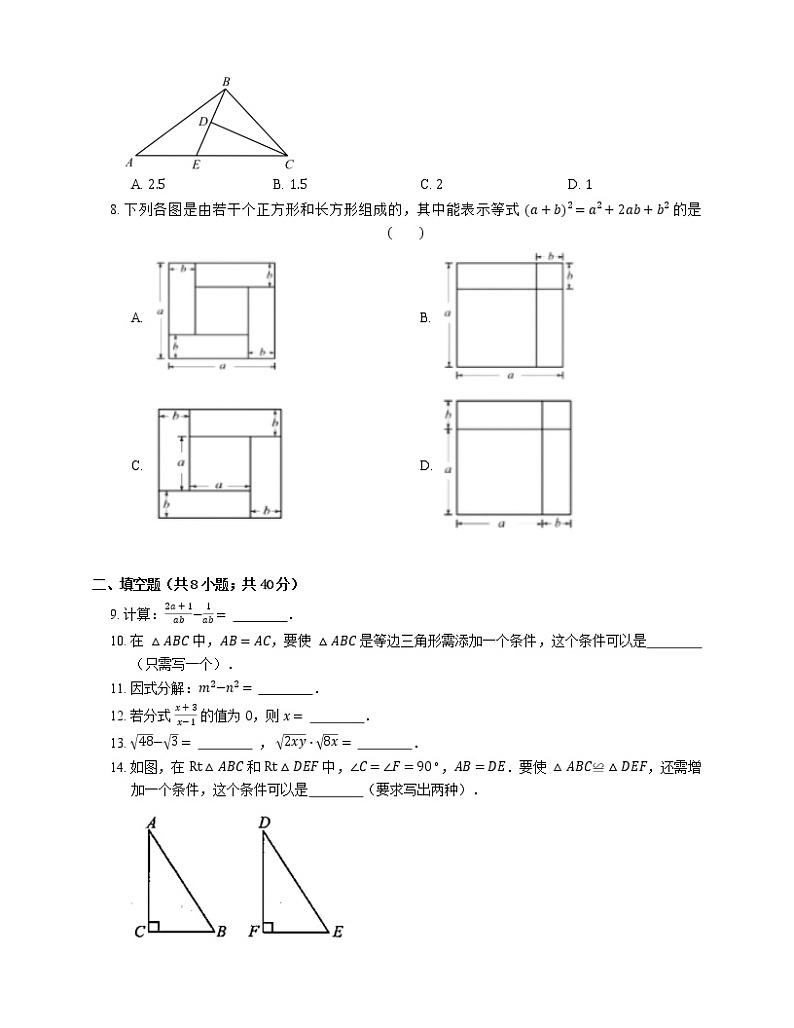
7. 如图，D 为 △ABC 内一点，CD 平分 ∠ACB，BE⊥CD，垂足为 D，交 AC 于点 E，∠A=∠ABE．若 AC=5，BC=3，则 BD 的长为
A. 2.5B. 1.5C. 2D. 1

8. 下列各图是由若干个正方形和长方形组成的，其中能表示等式 a+b2=a2+2ab+b2 的是
A. B.
C. D.

二、填空题（共8小题；共40分）
9. 计算：2a+1ab−1ab= ．

10. 在 △ABC 中，AB=AC，要使 △ABC 是等边三角形需添加一个条件，这个条件可以是 （只需写一个）．

11. 因式分解：m2−n2= ．

12. 若分式 x+3x−1 的值为 0，则 x= ．

13. 48−3= ， 2xy⋅8x= ．

14. 如图，在 Rt△ABC 和 Rt△DEF 中，∠C=∠F=90∘，AB=DE．要使 △ABC≌△DEF，还需增加一个条件，这个条件可以是 （要求写出两种）．

15. 已知 a2+2a=−2，则 2a2a+1+a+42 的值为 ．

16. 如图，学校需要测量旗杆的高度．同学们发现系在旗杆顶端的绳子垂到了地面，并多出了一段．同学们首先测量了多出的这段绳子长度为 1 m，然后将这根绳子拉直，当绳子的另一端和地面接触时，绳子与旗杆的底端距离恰好为 5 m，利用勾股定理求出旗杆的高度约为 m．

三、解答题（共12小题；共156分）
17. 计算：24÷3−12×10+20．

18. 分解因式：a4b4+a2b2−20．

19. 解方程：2−xx−3=1−13−x．

20. 如图，已知 BD=CE，AB=AC，点 A 是 DE 的中点，说明 △ABD 与 △ACE 全等的理由．

21. 已知，如图，点 A 、点 B 在直线 l 异侧，以点 A 为圆心，AB 长为半径作弧交直线 l 于 C，D 两点．分别以 C，D 为圆心，AB 长为半径作弧，两弧在 l 下方交于点 E，连接 AE．
（1）根据题意，利用直尺和圆规补全图形；
（2）证明：l 垂直平分 AE．

22. 依法纳税是每个公民应尽的义务．新税法规定：居民个人的综合所得，以每一纳税月收入减去费用 5000 元以及专项扣除、专项附加扣除和依法确定的其他扣除后的余额，为个人应纳税所得额．已知李先生某月的个人应纳税所得额比张先生的多 1500 元，个人所得税税率相同情况下，李先生的个人所得税税额为 76.5 元，而张先生的个人所得税税额为 31.5 元．求李先生和张先生应纳税所得额分别为多少元?个人所得税税率=个人所得税税额应纳税所得额

23. 如图，在正方形网格中，每个小正方形的边长均为 1，线段 AB 的端点在格点上，按要求画图．
（1）在图①中找出一个格点 M，使 △ABM 是面积最小的直角三角形，画出这个直角三角形，并直接写出它的面积为 ．
（2）在图②中找出一个格点 N，使 △ABN 是面积最大的直角三角形，画出这个直角三角形，并直接写出它的面积为 ．

24. 如图，△ABC 三个顶点的坐标分别为 A1,1，B4,2，C3,4．
（1）请画出 △ABC 关于 x 轴成轴对称的图形 △A1B1C1，并写出 A1，B1，C1 的坐标；
（2）在 y 轴上找一点 P，使 PA+PB 的值最小，请画出点 P 的位置．

25. 先化简，后求值：x2+1x2−x−2x−1÷x+1x，其中 x=2．

26. 请仔细阅读下面某同学对多项式 x2−4x+2x2−4x+6+4 进行因式分解的过程，然后回答问题：
解：令 x2−4x+2=y，则
原式=yy+4+4第一步=y2+4y+4第二步=y+22第三步=x2−4x+42.第四步
（1）该同学第二步到第三步运用了因式分解的
A．提取公因式
B．平方差公式
C．两数和的完全平方公式
D．两数差的完全平方公式
（2）另外一名同学发现第四步因式分解的结果不彻底，请你直接写出因式分解的最后结果： ；
（3）请你模仿以上方法尝试对多项式 x2−2xx2−2x+2+1 进行因式分解．

27. 如图，把一块等腰直角三角形零件（△ABC，其中 ∠ACB=90∘），放置在一凹槽内，三个顶点 A，B，C 分别落在凹槽内壁上，已知 ∠ADE=∠BED=90∘，测得 AD=5 cm，BE=7 cm，求该三角形零件的面积．

28. 在公式 s=v0t+12at2 中，所有字母均为正数．
（1）用 s，a，t 表示 v0；
（2）当 s=24，a=9，t=2 时，求 v0 的值．
答案
第一部分
1. C【解析】三角形中，到三边距离相等的点是三条角平分线的交点．
2. C【解析】选项A，B，D都是轴对称图形，且对称轴都是竖直的，选项C的图形的轮廓也是轴对称图形，但内部图案不是轴对称图形（是中心对称图形）．
故选C．
3. B【解析】将 0.0000005 用科学记数法表示为 5×10−7 ．
4. B【解析】根据题意，代数式要有意义，必须满足 x+3>0 且 4−3x≥0，即 −35. D
6. B【解析】∵△ABC≌△ADE，
∴AC=AE，AB=AD，∠ABC=∠ADE，∠BAC=∠DAE，
∴∠BAC−∠DAC=∠DAE−∠DAC，
∴∠BAD=∠CAE．
故A，C，D选项错误，B选项正确．
7. D
8. D【解析】A选项中整体面积 =a2，分部面积 =a−2b2+4ba−b，即得到的是 a2=a−2b2+4ba−b，故A选项错误；
B选项中整体面积 =a2，分部面积 =a−b2+2ba−b+b2，即得到的是 a2=a−b2+2ba−b+b2，故B选项错误；
C选项中整体面积 =2b+a2，分部面积 =a2+4ba+b，即得到是 2b+a2=a2+4ba+b，故C选项错误；
D选项中整体面积 =a+b2，分部面积 =a2+2ab+b2，即得到的是 a+b2=a2+2ab+b2，故选D．
第二部分
9. 2b
【解析】2a+1ab−1ab=2aab=2b．
10. AB=BC 或 ∠A=60∘ 等
11. m+nm−n
12. −3
13. 33，4xy
14. BC=EF 或 AC=DF 或 ∠A=∠D 或 ∠B=∠E
15. 6
【解析】原式=4a2+2a+a2+8a+16=5a2+10a+16=5a2+2a+16,
∵a2+2a=−2，
∴原式=−10+16=6．
16. 12
第三部分
17. 原式=24÷3−12×10+25=8−5+25=22+5.
18. a2b2+5ab−2ab+2．
19. 方程两边乘 x−3，得
2−x=x−3+1.
解得
x=2.
经检验，x=2 是原分式方程的解．
20. 因为点 A 是线段 DE 中点（已知），
所以 DA=EA（线段中点的意义），
在 △ABD 与 △ACE 中，
BD=CE已知,DA=EA,AB=AC已知,
所以 △ABD≌△ACESSS．
21. （1） 补图如下：
（2） 如图，连接 AC，AB，CE，ED，AD，
∵AC=AD=AB，CE=ED=AB，
∴AC=CE，AD=DE，
∴C，D 在 AE 的垂直平分线上，
∴l 垂直平分 AE．
22. 设张先生应纳税所得额为 x 元，则李先生应纳税所得额为 x+1500 元．
依题意得，
76.5x+1500=31.5x.
解得
x=1050.
经检验：x=1050 是原方程的根且符合题意，
当 x=1050 时，x+1500=2550，
答：李先生和张先生的应纳税所得额分别为 2550 元，1050 元．
23. （1）
1.5
【解析】S△ABM=12×1×3=1.5．
（2）
2.5
【解析】S△ABN=12×5×5=2.5．
24. （1） 如图所示，△A1B1C1 即为所求，
由图知，A1 的坐标为 1,−1，B1 的坐标为 4,−2，C1 的坐标为 3,−4；
（2） 如图所示，点 P 即为所求．
25. x2+1x2−x−2x−1÷x+1x=x2−2x+1xx−1÷x+1x=x−12xx−1⋅xx+1=x−1x+1,
当 x=2 时，
原式=2−12+1=13.
26. （1） C
（2） x−24
（3） 令 x2−2x=y，
则 原式=yy+2+1=y2+2y+1=y+12=x2−2x+12=x−14．
27. ∵ △ABC 是等腰直角三角形，
∴ AC=BC，∠ACB=90∘，
∴ ∠ACD+∠BCE=90∘，
∵ ∠ADC=90∘，
∴ ∠ACD+∠DAC=90∘，
∴ ∠DAC=∠BCE，
在 △ADC 和 △CEB 中，
∠D=∠E,∠DAC=∠ECB,AC=CB,
∴ △ADC≌△CEBAAS，
∴ DC=BE=7 cm，
∴ AC=52+72=25+49=74cm，
∴ BC=74，
∴ 该零件的面积为：12×74×74=37cm2．
28. （1） 2s−at22t
（2） 3