沪科版八年级下册19.1 多边形内角和优秀ppt课件

这是一份沪科版八年级下册19.1 多边形内角和优秀ppt课件，文件包含191多边形内角和ppt、191多边形内角和同步练习doc、191多边形内角和教学设计doc等3份课件配套教学资源，其中PPT共35页， 欢迎下载使用。

三角形是由三条不在同一条直线上的线段首尾顺次连结组成的平面图形 .
问题2：三角形有几条边？几个顶点？几个角？三角形内角和是多少度？
问题1：什么叫三角形？
三角形有3条边，3个顶点,3个角，三角形内角和 180°。
你能根据三角形的定义，说出什么叫四边形吗？
四边形是由四条不在同一直线上的线段首尾顺次连结组成的平面图形，记为四边形ABCD
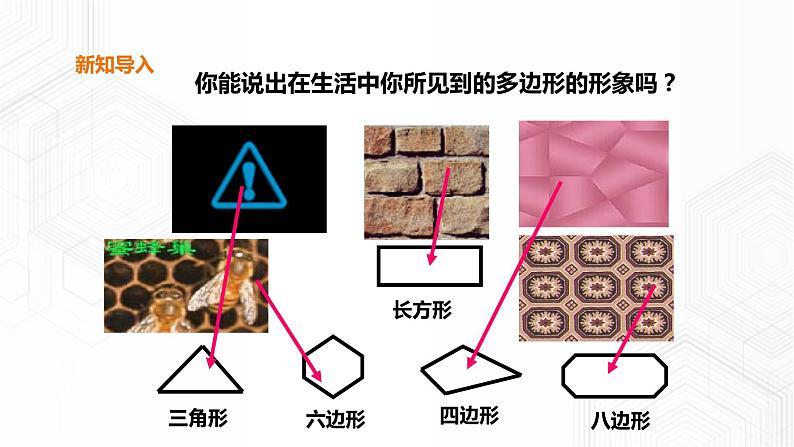
你能说出在生活中你所见到的多边形的形象吗？
在定义中应注意：①若干条； ②首尾顺次相连，二者缺一不可.
在平面内，由若干条不在同一条直线上的线段首尾顺次相接组成的封闭的图形叫做多边形.
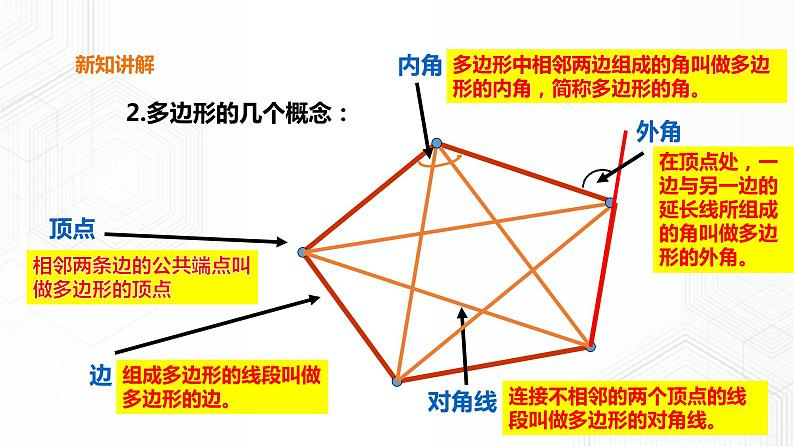
2.多边形的几个概念：
组成多边形的线段叫做多边形的边。
相邻两条边的公共端点叫做多边形的顶点
多边形中相邻两边组成的角叫做多边形的内角，简称多边形的角。
在顶点处，一边与另一边的延长线所组成的角叫做多边形的外角。
连接不相邻的两个顶点的线段叫做多边形的对角线。
如图（1）就叫做四边形ABCD。图（2）就叫做五边形ABCDE。三角形、四边形都属于多边形，其中三角形是边数最少的多边形。三角形有三条边，四边形有四条边，n边形有n条边，n个顶点，n个内角.
3、多边形的命名与表示：
多边形一般按边数来命名，有几条边就叫做几边形，并用它的各个顶点的大写字母顺次排列来表示.
一个多边形，如果把它的任何一边双向延长，其它的各边都在延长线所得直线的同一旁，这样的多边形叫做凸多边形。
我们现在研究的是如图(1)所示的多边形，是凸多边形； 如图(2)所示的多边形，是凹多边形，但不是现在研究的范围中．今后如果不说明，我们讲的多边形都是凸多边形．
任意一个四边形的内角和是多少度？
请同学们任意画一个四边形，用量角器量一下各个内角的度数，计算一下四边形的内角和.
如图所示，利用辅助线将四边形分割成两个三角形
你能利用三角形内角和定理证明四边形的内角和等于360 °吗？
四边形ABCD的内角和＝ ∆ ABC的内角和 + ∆ ACD的内角和 ＝ 180 °+ 180 °＝ 360 °
解题思路：四边形问题转化为三角形问题来解决．
因为四边形被分割成4个三角形，有四个不是四边形内角的角组成了一个周角，所以四边形内角和＝4×180°-360°
在四边形内任取一点，连接它与各个顶点，将四边形分割成4个三角形，
五边形的内角和又是多少呢？
五边形的内角和是___　　____
你还有其他的方法计算五边形的内角和吗？
（n－2）×180°
n边形的内角和＝（n－2）·180°
探索多（n）边形的内角和
方法一：由多边形一个顶点引对角线分割三角形
对角线是解决多边形问题的常用辅助线
从n边形的一个顶点出发，向自身和 相邻的两个顶点无法引对角线，向其他顶点共引(n－3)条对角线，这时n边形被分割成(n－2)个三角形，因为每个三角形的内角和是180°，所以n边形的内角和为(n－2)•180°
该图中n边形共有n个三角形，故所有三角形内角和为n×180 °，但每个图中都有一个以红圈圈住的点，它是一个圆周角360 °，因此n边形的内角和为 n×180 °- 360 °= (n-2)×180 °
方法二：在多边形的内部任取一点分割三角形
这种分割方式，将多边形分成n-1个三角形，故所有三角形的内角和为（n-1）×180 °，边上一点周围所形成的平角不是多边形的内角，因此n边形的内角和为 （n-1）×180 °- 180 °= (n-2)×180 °
方法三：在多边形一条边上任取一点分割三角形
该图中n边形共有n-1个不重叠的三角形，故所有三角形内角和为（n-1）×180 °，但每个图中都多了一个三角形的内角和，因此n边形的内角和为 （n-1）×180 °- 180 °= (n-2)×180 °
方法四：在多边形的外部任取一点分割三角形
上面研究了多边形的内角和，在多边形的每个顶点处取多边形的一个外角，它们的和叫做多边形的外角和，多边形外角和又有怎样的规律呢？
5.多边形内角和定理：n边形的内角和等于（n-2）×180°（n为不小于3的整数）.
6.多边形外角和定理：n边形的外角和等于360°（n为不小于3的整数）.
多边形中如果各条边都相等，各个内角都像你这样的多边形，叫做正多边形，例如正三角形，正方形，正五边形，正六边形等等
例1 一个多边形的内角和为1440°，求这个多边形的边数.
分析：设多边形的边数为n,根据内角和定理列方程即可求出n.
解：设多边形的边数为n,根据题意可得(n-2)180°=1440°解得a=10答:把这个多边形的边数为10.
例2、求正六边形每个内角的度数.
分析：这种多边形的内角和定理，求出正六边形的内角和，再结合其边数，即可求解.
解：因为正六边形的内角和为(6-2) ×180°=720°,所以每个内角的度数为720°÷ 6=120°.
1、12边形的内角和等于_______
解：由多边形内角和定理可得,（n-2) ×180°=（12-2）×180°=1800°
2、如果一个多边形的内角和等于1800°，那么这是_　__边形
解:设这个多边形为n边形，由题意可得，(n-2)×180°=1800°
所以这个多边形为十二边形。
3、下列角度中，不能成为多边形的内角和的是（ ）（A）540° （B）580° （C）1800° （D）900°
解:多边形内角和公式为(n-2)×180°，所以多边形内角和一定为180的倍数，故选择B.
1.(2018南通）若一个凸多边形的内角和为720度，则这个多边形的边数为（ ）Ａ4　　 Ｂ. 5　 　Ｃ.6　　 　Ｄ7
【分析】设这个多边形的边数为n，根据多边形的内角和定理，可得方程，解方程，
解:设这个多边形的边数为n，根据多边形的内角和定理得
解得n=6，所以，这个多边形为六边形，
(n-2)×180°=720°，
2.(2018同仁）如果一个多边形的内角和是外角和的三倍，则这个多边形的边数是（ ）Ａ8　　 Ｂ. 9　　 Ｃ.10　　　 Ｄ11
【分析】根据多边形内角和公式及外角的特征计算即可.
解:因为这个多边形的外角和是360度,根据题意，得
解得n=8，所以，这个多边形为八边形，
(n-2)×180°=3×360°，
3.(2018济南）一个正多边形的每个内角等于108度，则它的边数是　　　　.
【分析】根据相邻的内角与外角互为邻补角求出，每一个外角的度数为72度，再用外角和，360度除以720度，计算即可，得结果.
解:设正多边形的边数为n ，外角的度数是:180 ° -108 °=72 °
则n=360°÷72°=5，
1、我们学会了许多解决数学问题的思想方法，如将多边形问题转化为三角形问题，以及类比方法，化未知为已知的转化思想方法等。2、通过探索多边形的内角和公式，我们尝试了从不同的角度寻求解决问题的方法，并且能有效地解决问题。3、我们还学会了运用多边形内角和公式及多边形对角线条数公式进行相关计算。
在平面内，由若干条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形.
2、n边形的内角和是多少？
n边形的内角和等于(n - 2)•180°.它揭示了多边形的内角和与边数之间的关系.
1.必做作业：课本P74 习题 19.1 第1、5题
2.选做作业：课本P74 习题 19.1　第7题