第19章四边形19.1多边形内角和第1课时多边形的内角和课件（沪科版八下）

这是一份第19章四边形19.1多边形内角和第1课时多边形的内角和课件（沪科版八下），共23页。

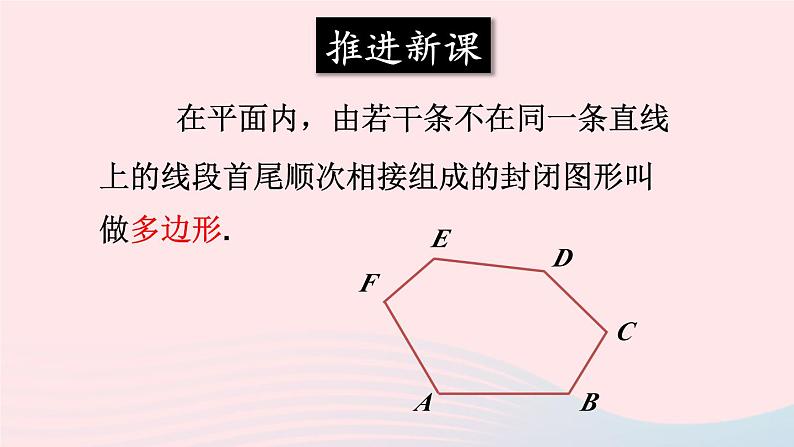
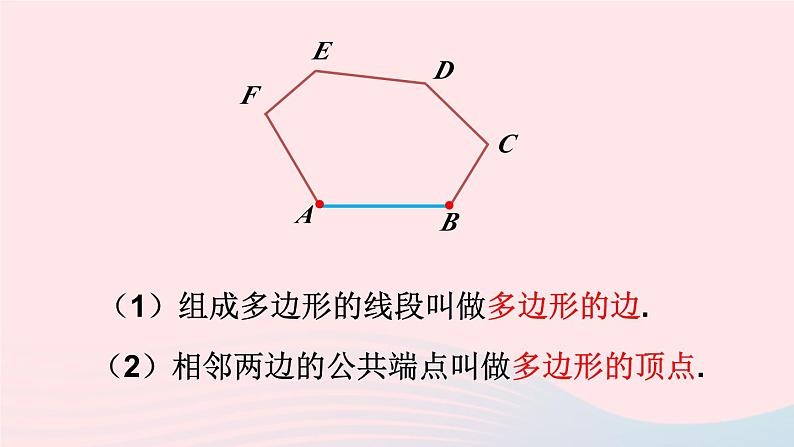
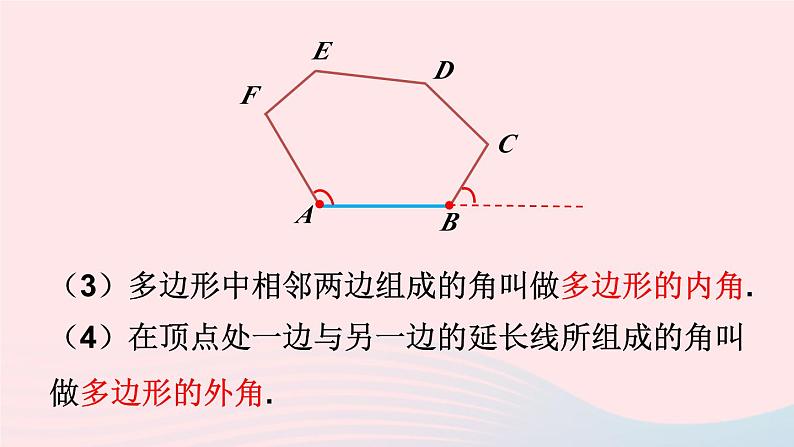
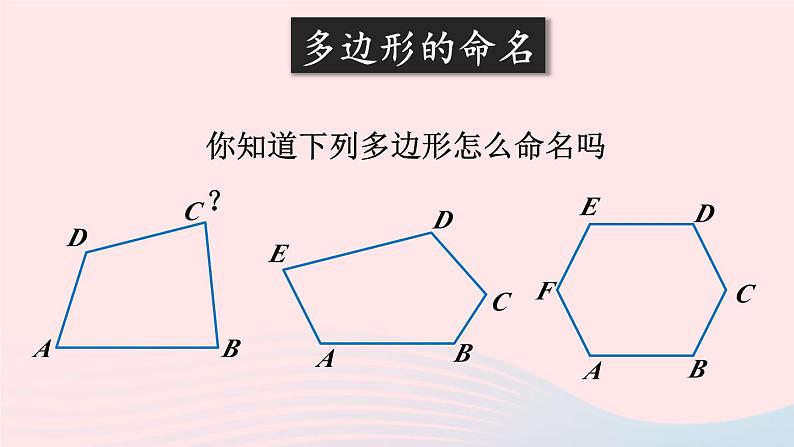
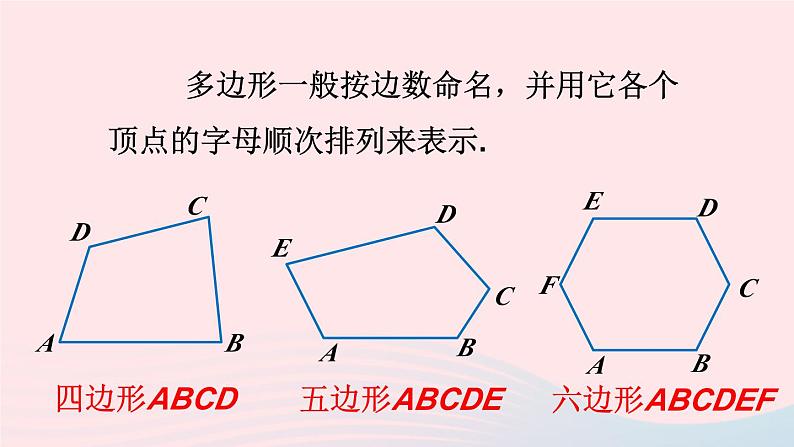
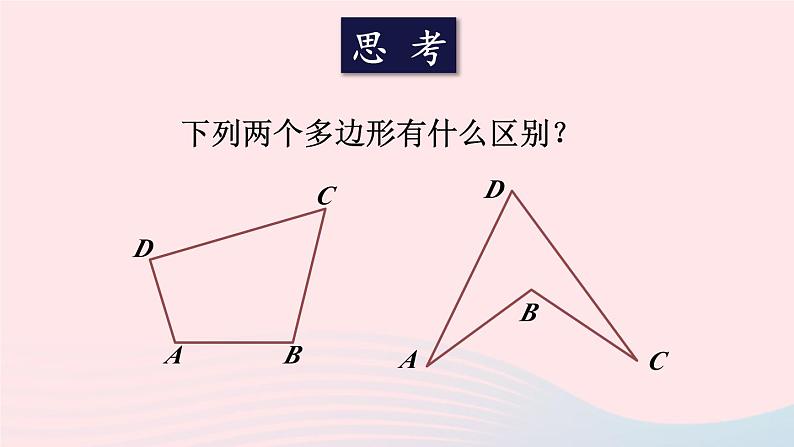
沪科版·八年级数学下册第19章 四边形19.1 多边形内角和第1课时 多边形内角和新课导入观察下列图形，说一说什么是多边形？推进新课 在平面内，由若干条不在同一条直线上的线段首尾顺次相接组成的封闭图形叫做多边形.ABCDEF（1）组成多边形的线段叫做多边形的边.（2）相邻两边的公共端点叫做多边形的顶点.（3）多边形中相邻两边组成的角叫做多边形的内角.（4）在顶点处一边与另一边的延长线所组成的角叫做多边形的外角.多边形的命名你知道下列多边形怎么命名吗？ 多边形一般按边数命名，并用它各个顶点的字母顺次排列来表示.四边形ABCD五边形ABCDE六边形ABCDEF思 考下列两个多边形有什么区别？ 一个多边形，如果把它任何一边双向延长，其他各边都在延长所得直线的同一旁，这样的多边形就是凸多边形.探究多边形的内角和 多边形中连接不相邻两个顶点的线段叫做多边形的对角线. 过 n 边形的一个顶点有_____条对角线，n 边形共有_______条对角线.n-3 我们知道，三角形的内角和为180°，你知道四边形、五边形、六边形的和分别是多少吗？方法一： 从四边形的一个顶点出发作对角线，将四边形分成两个三角形.四边形的内角和等于两个三角形内角和之和：180°×2 = 360°五边形的内角和等于 3 个三角形内角和之和：180°×3 = 540°六边形的内角和等于 4 个三角形内角和之和：180°×4 = 720°你知道 n 边形的内角和怎么求吗？1180°2360°3540°4720°n-2(n-2)×180°方法二： 在四边形内任取一点O，连接OA，OB，OC，OD，得到四个三角形.O四边形的内角和等于 4 个三角形内角和之和，减去一个圆周角：180°×4 - 360° = 360°O五边形的内角和等于 5 个三角形内角和之和，减去一个圆周角：180°×5 - 360° = 540°O六边形的内角和等于 6 个三角形内角和之和，减去一个圆周角：180°×6 - 360° = 720°结 论一般地，n 边形的内角和是多少呢？随堂练习1.____边形内角和是四边形内角和的2倍.2一个多边形的边数增加1，则内角和增加的度数是______.六180°3.已知多边形内角和等于1 080°，求它的边数.解：设多边形的边数为 n.(n-2)·180°= 1080° n = 8答：多边形的边数为8. 4.已知多边形每个内角都等于150°，求它的边数及内角和.解：设多边形的边数为n，则内角和等于n ·150°.(n-2)·180°= n·150° n = 12内角和：150°×12 = 1800°. 5. 过某个多边形一个顶点的所有对角线，将这个多边形分成 5 个三角形。这个多边形是几边形？它的内角和是多少？多边形的边数为7，内角和等于900°.