中考数学新突破复习第三章函数3.4二次函数的图象与性质优质课件PPT

这是一份中考数学新突破复习第三章函数3.4二次函数的图象与性质优质课件PPT，共23页。PPT课件主要包含了知识要点·归纳，►知识点一二次函数，三年中考·讲练，谢谢观看等内容，欢迎下载使用。

1．二次函数的概念一般地，如果y＝ax2＋bx＋c(a　≠　0，a、b、c为____数)，那么y叫做x的二次函数．【注意】(1)二次函数的表达式为整式，且二次项系数________；(2)b，c可分别为0，也可同时为0；(3)自变量的取值范围是__________．
2．二次函数的三种表达式(1)一般式：y＝___________________，这种形式只能看出二次函数图象的开口方向．当知道三点坐标求解析式时，设出一般式．(2)顶点式：y＝__________________，这种形式不但能看出二次函数图象的开口方向，还能看出它的对称轴x＝h，顶点坐标(h，k)，最值k.当知道顶点坐标和另一点坐标求解析式时，设出顶点式．
ax2＋bx＋c(a≠0)
a(x－h)2＋k(a≠0)
a(x－x1)(x－x2)
3．确定二次函数解析式方法(1)若已知抛物线上三点的坐标，则可采用一般式y＝ax2＋bx＋c(a≠0)，利用待定系数法求得a，b，c的值．(2)若已知抛物线的顶点坐标或对称轴方程，则可采用顶点式：y＝a(x－h)2＋k(a≠0)，其中顶点坐标为(h，k)，对称轴为直线x＝h.(3)若已知抛物线与x轴交点的横坐标，则可采用交点式：y＝a(x－x1)(x－x2)(a≠0)，其中与x轴的交点坐标为(x1,0)，(x2,0)．
二次函数的图象是一条________，它与x轴有三种位置关系，分别是________________________________．
►知识点二　二次函数的图象与性质
有两个交点，有一个交点，无交点
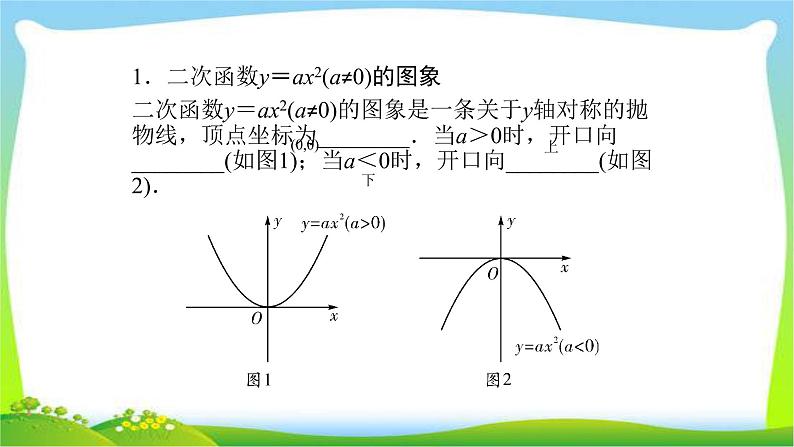
1．二次函数y＝ax2(a≠0)的图象二次函数y＝ax2(a≠0)的图象是一条关于y轴对称的抛物线，顶点坐标为________．当a＞0时，开口向________(如图1)；当a＜0时，开口向________(如图2)．
2．二次函数y＝ax2＋bx＋c(a≠0)的图象与性质
3.二次函数y＝ax2＋bx＋c图象的画法五点绘图法：利用配方法将二次函数y＝ax2＋bx＋c化为顶点式y＝a(x－h)2＋k，确定其开口方向，对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图．一般选取五点：顶点，与y轴的交点(0，c)，(0，c)关于对称轴对称的点(2h，c)，与x轴的交点(x1,0)，(x2,0)(若与x轴没有交点，则取两组关于对称轴对称的点)．画草图时应抓住以下几点：开口方向，对称轴，顶点，与x轴的交点，与y轴的交点．
二次函数解析式的确定
【思路点拨】　本题考查了待定系数法求二次函数解析式，以及二次函数图象上点的坐标特征．(1)根据题意确定出B与C的坐标，代入抛物线解析式求出b与c的值，即可确定出解析式；(2)把抛物线解析式化为顶点形式，找出顶点坐标，四边形ABDC面积＝三角形ABC面积＋三角形BCD面积，求出即可．
【例2】　(2015·陕西)下列关于二次函数y＝ax2－2ax＋1(a＞1)的图象与x轴交点的判断，正确的是(　　)A．没有交点B．只有一个交点，且它位于y轴右侧C．有两个交点，且它们均位于y轴左侧D．有两个交点，且它们均位于y轴右侧【思路点拨】　本题考查二次函数的图象及抛物线与坐标轴的交点问题．根据函数值为零，可得相应的方程，根据根的判别式，公式法求方程的根，可得答案．
二次函数的图象与性质
数形结合思想：数和形是数学中的两种表现形式，是把数量关系和图形结合起来研究，把代数问题结合几何问题求解，或把几何问题用数学语言表示出来进行解答，解答时要注意题中的数与图中的点相互结合.
二次函数图象平移法则
【错解分析】　抛物线y＝－3x2＋9x由y＝－3x2平移而得，容易得出y＝－3x2＋9x是y＝－3x2向右平移3个单位，再向上平移9个单位得到的．