4.6 指数函数与对数函数复习课 教学设计

4.6指数函数与对数函数（复习课）

(人教A版普通高中教科书数学必修第一册第四章)

一、教学目标

1. 了解指数函数、指数函数的图象，理解指数函数、对数函数的单调性，特殊点等性质，并能简单应用．

2.了解指数函数y＝ax与对数函数y＝logax(a>0，且a≠1)互为反函数，掌握反函数的求法.

3. 理解函数与方程的联系，掌握数形结合的思想方法.

二、教学重难点

1.重点：指数函数、对数函数的单调性，图像与性质.

2.难点：与指数、对数函数有关的函数值域和复合函数的单调性问题.

三、教学过程

1.知识梳理

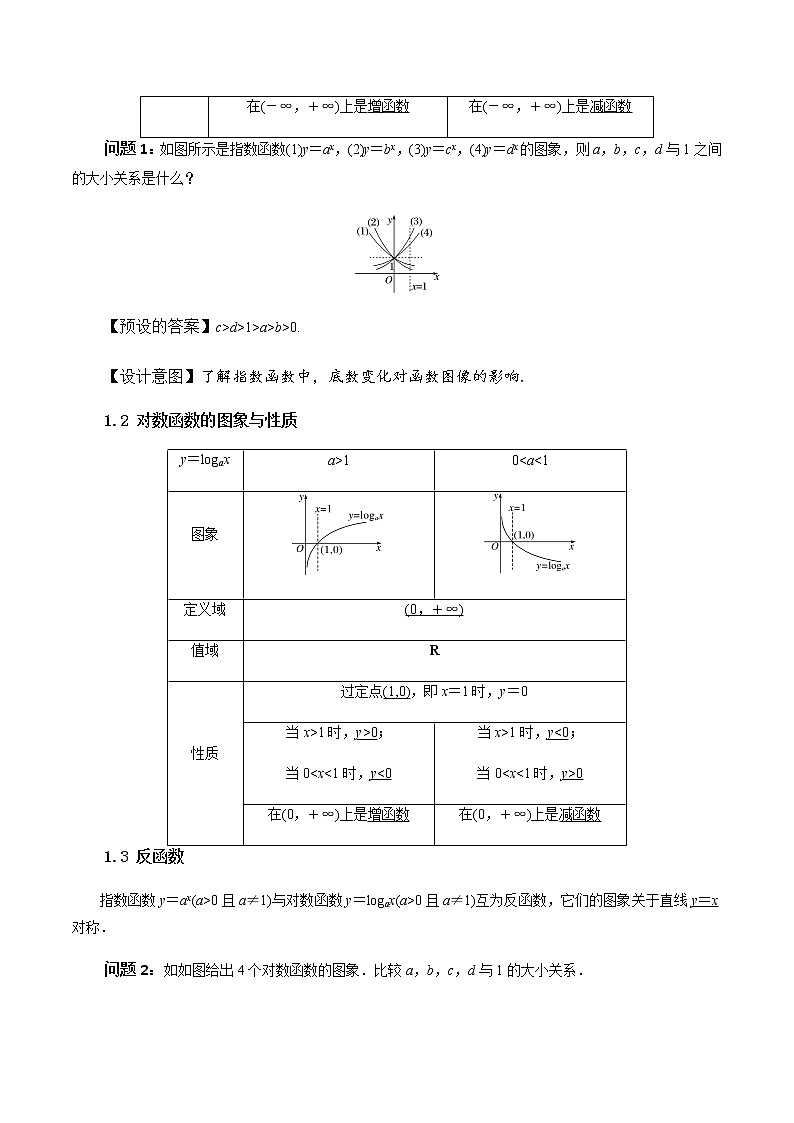
1.1 指数函数及其性质

问题1：如图所示是指数函数(1)y＝ax，(2)y＝bx，(3)y＝cx，(4)y＝dx的图象，则a，b，c，d与1之间的大小关系是什么？

【预设的答案】c>d>1>a>b>0.

【设计意图】了解指数函数中，底数变化对函数图像的影响.

1.2 对数函数的图象与性质

1.3 反函数

指数函数y＝ax(a>0且a≠1)与对数函数y＝logax(a>0且a≠1)互为反函数，它们的图象关于直线y＝x对称．

问题2：如如图给出4个对数函数的图象．比较a，b，c，d与1的大小关系．

【预设的答案】　0<c<d<1<a<b.

【设计意图】了解对数函数中，底数变化对函数图像的影响.

2.题型探究

题型一：指数函数的图象与性质

命题点1　比较指数式的大小

例1. (多选)已知实数a，b满足等式2 021a＝2 022b，下列等式可以成立的是(　　)

A．a＝b＝0   B．a<b<0

C．0<a<b   D．0<b<a

【预设的答案】ABD

解析　如图，观察易知，a<b<0或0<b<a或a＝b＝0，故选ABD.

【设计意图】有关指数方程、不等式问题的求解，往往利用相应的指数型函数图象，数形结合求解．

命题点2　指数型函数的图像

例2. 若函数f(x)＝|2x－2|－b有两个零点，则实数b的取值范围是________．

【预设的答案】(0,2)

解析　在同一平面直角坐标系中画出y＝|2x－2|与y＝b的图象，如图所示．

∴当0<b<2时，两函数图象有两个交点，从而函数f(x)＝|2x－2|－b有两个零点．

∴b的取值范围是(0,2)．

【设计意图】 (1)对于有关指数型函数的图象问题，一般是从最基本的指数函数的图象入手，通过平移、伸缩、对称变换得到．特别地，当底数a与1的大小关系不确定时应注意分类讨论．

(2)有关指数方程、不等式问题的求解，往往利用相应的指数型函数图象，数形结合求解．

命题点3　解简单的指数不等式

例3. 若，则函数y＝2x的值域是(　　)

A.   B.

C.   D．[2，＋∞)

【预设的答案】B

解析　x－2＝(2－2)x－2＝2－2x＋4，

∴

即x2＋1≤－2x＋4，即x2＋2x－3≤0，

∴－3≤x≤1，此时y＝2x的值域为[2－3，21]，

即为.

【设计意图】利用指数函数的性质比较大小或解方程、不等式，最重要的是“同底”原则，比较大小还可以借助中间量．

题型二：对数函数的图象与性质

命题点1　比较指数式、对数式的大小

例4. (1)设a＝log3e，b＝e1.5，，则(　　)

A．b<a<c   B．c<a<b

C．c<b<a   D．a<c<b

【预设的答案】D

解析　＝log34>log3e＝a.

又c＝log34<log39＝2，b＝e1.5>2，

∴a<c<b.

(2)若实数a，b，c满足loga2<logb2<logc2<0，则下列关系中正确的是(　　)

A．a<b<c   B．b<a<c

C．c<b<a   D．a<c<b

【预设的答案】C

解析　根据不等式的性质和对数的换底公式可得

<<<0，

即log2c<log2b<log2a<0，

可得c<b<a<1.故选C.

【设计意图】(1)比较指数式和对数式的大小，可以利用函数的单调性，引入中间量；有时也可用数形结合的方法．

(2)解题时要根据实际情况来构造相应的函数，利用函数单调性进行比较，如果指数相同，而底数不同则构造幂函数，若底数相同而指数不同则构造指数函数，若引入中间量，一般选0或1.

命题点2　指数函数、对数函数的综合应用

例5. 设已知函数f(x)＝loga(2x＋b－1)(a>0，且a≠1)的图象如图所示，则a，b满足的关系是(　　)

A．0<a－1<b<1   B．0<b<a－1<1

C．0<b－1<a<1   D．0<a－1<b－1<1

【预设的答案】A

解析　由函数图象可知，f(x)为增函数，故a>1.函数图象与y轴的交点坐标为(0，logab)，由函数图象可知－1<logab<0，解得<b<1.

综上有0<<b<1.

【设计意图】在识别函数图象时，要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项．

命题点2　指数函数、对数函数的综合应用

例6. 若方程4x＝logax在上有解，则实数a的取值范围为__________．

【预设的答案】

解析　若方程4x＝logax在上有解，则函数y＝4x和函数y＝logax在上有交点，

由图象知解得0<a≤.

【设计意图】一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．

题型三：反函数的应用

例7. 设函数y＝f(x)的图象与y＝x＋a的图象关于直线y＝x对称，且f(3)＋f ＝4，则实数a＝________.

【预设的答案】－2

解析　设(x，y)是y＝f(x)图象上任意一点，则(y，x)在函数y＝x＋a的图象上．

所以x＝y＋a，则.

因此.

由f(3)＋f ＝4，得－1＋1－2a＝4，所以a＝－2.

【设计意图】了解指数函数y＝ax与对数函数y＝logax(a>0，且a≠1)互为反函数，并掌握反函数的求法.

题型四：复合函数的应用

例8. 函数.若f(x)在(－∞，－3)上单调递减，则a的取值范围是________．

【预设的答案】

解析　令t＝ax2－4x＋3，则y＝t，

∵y＝t为减函数，

∴t＝ax2－4x＋3在(－∞，－3)上单调递增，

则

解得a≤－.

例9. 已知函数f(x)＝loga(8－ax)(a>0，且a≠1)，若f(x)>1在区间[1,2]上恒成立，则实数a的取值范围是__________．

【预设的答案】

解析　当a>1时，f(x)＝loga(8－ax)在[1,2]上单调递减，由f(x)>1在区间[1,2]上恒成立，

则f(x)min＝f(2)＝loga(8－2a)>1，且8－2a>0，

解得1<a<.

当0<a<1时，f(x)在[1,2]上单调递增，

由f(x)>1在区间[1,2]上恒成立，

知f(x)min＝f(1)＝loga(8－a)>1，且8－2a>0.

解得a∈∅，

综上可知，实数a的取值范围是.

【设计意图】

求与指数、对数函数有关的函数值域和复合函数的单调性问题，必须弄清三方面的问题：一是定义域，所有问题都必须在定义域内讨论；二是底数与1的大小关系；三是复合函数的构成，即它是由哪些基本初等函数复合而成的，借助“同增异减”这一性质分析判断．另外，解题时要注意数形结合、分类讨论、转化与化归思想的应用．

3.归纳小结，文化渗透

思考：本节课你有哪些收获？

【设计意图】

（1）让学生学会自主梳理本节课的学习内容、解题方法、数学思想；

（2）鼓励学生不怕困难，积极攀登知识高峰.

四、课外作业