2020-2021学年2.4 等比数列教学设计

等比数列

教学内容分析

这节课是在等差数列的基础上，运用同样的研究方法和研究步骤，研究另一种特殊数列———等比数列．重点是等比数列的定义和通项公式的发现过程及应用，难点是应用．

教学目标

1. 熟练掌握等比数列的定义、通项公式等基本知识，并熟练加以运用．

2. 进一步培养学生的类比、推理、抽象、概括、归纳、猜想能力．

3. 感受等比数列丰富的现实背景，进一步培养学生对数学学习的积极情感．

任务分析

这节内容由于是在等差数列的基础上，运用同样的方法和步骤，研究类似的问题，学生接受起来较为容易，所以应多放手让学生思考，并注意运用类比思想，这样不仅有利于学生分清等差和等比数列的区别，而且可以锻炼学生从多角度、多层次分析和解决问题的能力．另外，与等差数列相比等比数列须要注意的细节较多，如没有零项、ｑ≠0等，在教学中应注意加以比较．

教学设计

一、问题情景

在前面我们学习了等差数列，在现实生活中，我们还会遇到下面的特殊数列：

1. 在现实生活中，经常会遇到下面一类特殊数列．下图是某种细胞分裂的模型．

细胞分裂个数可以组成下面的数列：

1，2，4，8，…

2. 一种计算机病毒可以查找计算机中的地址薄，通过电子函件进行传播．如果把病毒制造者发送病毒称为第一轮，函件接收者发送病毒称为第二轮，依此类推．假设每一轮每一台计算机都感染20台计算机，那么，在不重复的情况下，这种病毒每一轮感染的计算机数构成的数列是

1，20，202，203，…

（3）除了单利，银行还有一种支付利息的方式———复利，即把前一期的利息和本金加在一起算作本金，再计算下一期的利息，也就是通常说的“利滚利”．按照复利计算本利和的公式是

本利和＝本金×（1＋利率）存期

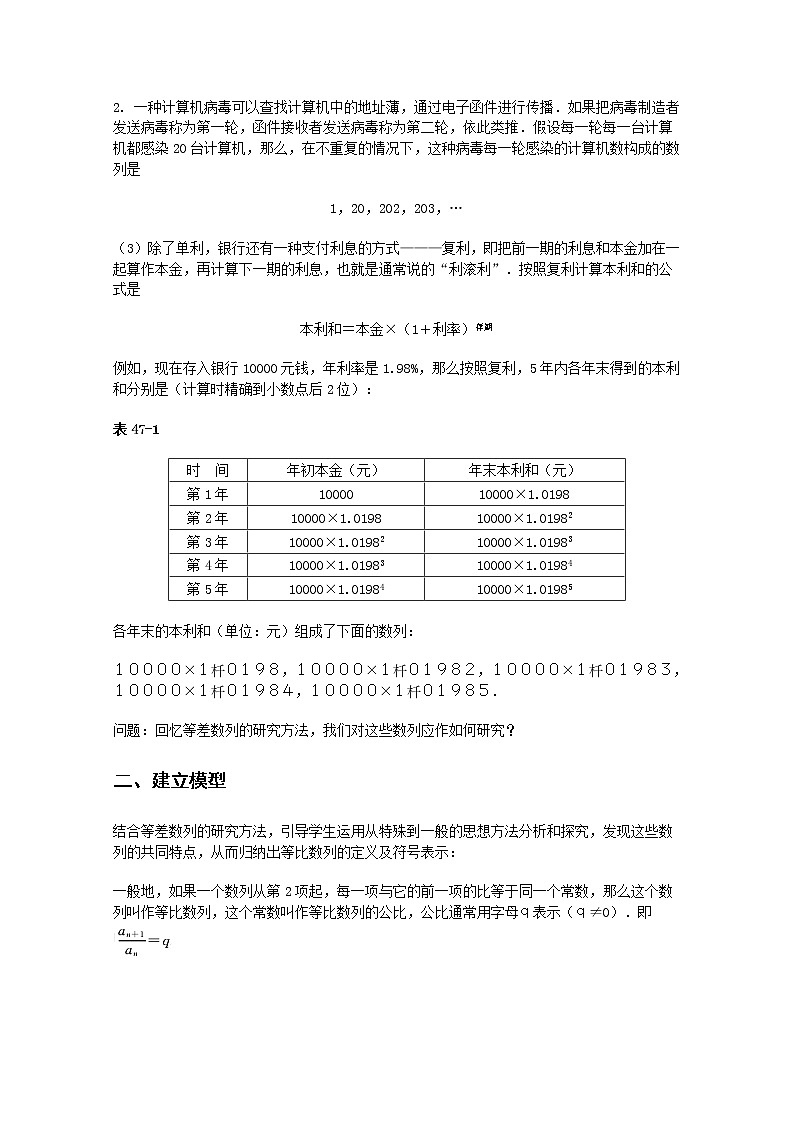
例如，现在存入银行10000元钱，年利率是1.98%，那么按照复利，5年内各年末得到的本利和分别是（计算时精确到小数点后2位）：

表47-1

各年末的本利和（单位：元）组成了下面的数列：

１００００×１０１９８，１００００×１０１９８２，１００００×１０１９８３，１００００×１０１９８４，１００００×１０１９８５．

问题：回忆等差数列的研究方法，我们对这些数列应作如何研究？

二、建立模型

结合等差数列的研究方法，引导学生运用从特殊到一般的思想方法分析和探究，发现这些数列的共同特点，从而归纳出等比数列的定义及符号表示：

一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列叫作等比数列，这个常数叫作等比数列的公比，公比通常用字母ｑ表示（ｑ≠0）．即

［问　题］

1. ｑ可以为0吗？有没有既是等差，又是等比的数列？

2. 运用类比的思想可以发现，等比数列的定义是把等差数列的定义中的“差”换成了“比”，同样，你能类比得出等比数列的通项公式吗？如果能得出，试用以上例子加以检验．

对于2，引导学生运用类比的方法：等差数列通项公式为ａｎ＝ａ１＋（ｎ－１）ｄ，即ａ１与（ｎ－１）个ｄ的和，等比数列的通项公式应为ａｎ等于ａ１与（ｎ－１）个ｑ的乘积，即ａｎ＝ａ１ｑｎ－１．上面的几个例子都满足通项公式．

3. 你如何论证上述公式的正确性．

证法1：同等差数列———归纳法．

证法2：类比等差数列，累乘可得，即

各式相乘，得ａn＝ａ1ｑn－1．

归纳特点：（1）ａn是关于ｎ的指数形式．

（2）和等差数列类似，通项公式中有ａn，ａ1，ｑ，ｎ四个量，知道其中三个量可求另一个量．

三、解释应用

［例　题］

1. 某种放射性物质不断衰变为其他物质，每经过一年剩留的这种物质是原来的84%，问：这种物质的半衰期为多长？

解：设这种物质最初的质量是1，经过ｎ年，剩留量是ａn．由已知条件，得数列｛ａn｝是一个等比数列，其中ａ1＝0.84，ｑ＝0.84．

设ａn＝0.5，则0.84n＝0.5．

两边取对数，得ｎｌｇ0.84＝ｌｇ0.5．

用计算器计算，得ｎ≈4．

答：这种物质的半衰期大约为4年．

2. 一个等比数列的第3项和第4项分别是12和18，求它的第1项与第2项．

解：设这个等比数列的第1项是ａ1，公比是ｑ，那么

注：例1、例2体现了方程思想的应用，这也是有关等差、等比数列运算中常用的思想方法．

3. 已知数列｛ａn｝，｛bn｝是项数相同的等比数列，那么｛ａnbn｝是否为等比数列？如果是，证明你的结论；如果不是，说明理由．

解：可以得到：如果｛ａn｝，｛bn｝是项数相同的等比数列，那么｛ａn·bn｝也是等比数列．

证明如下：

设数列｛ａn｝的公比为ｐ，｛bn｝的公比为ｑ，那么数列｛ａn·bn｝的第n项与第n＋1项分别为ａ1ｐn－1·ｂ1ｑn－1与ａ1ｐn·ｂ1ｑn，即ａ1ｂ1（ｐｑ）n－1与ａ1ｂ1（ｐｑ）n．两项相比，得

显然，它是一个与ｎ无关的常数，所以｛ａn·bn｝是一个以ｐｑ为公比的等比数列．

特别地，如果｛ａn｝是等比数列，ｃ是不等于0的常数，那么数列｛ｃ·ａn｝也是等比数列．

［练　习］

1. 在等比数列｛ａn｝中，

（1）ａ5＝４，ａ7＝６，求ａ9．

（2）ａ5－ａ1＝１５，ａ4－ａ2＝６，求ａ3．

2. 设｛ａn｝是正项等比数列，问：是等比数列吗？为什么？

3. 三个数成等比数列，并且它们的和等于14，它们的积等于64，求这三个数．

4. 设等比数列｛ａn｝，｛bn｝的公比分别是ｐ，ｑ．

（1）如果ｐ＝ｑ，那么｛ａn＋bn｝是等比数列吗？

（2）如果ｐ≠ｑ，那么｛ａn＋bn｝是等比数列吗？

四、拓展延伸

引导学生分析思考如下三个问题：

（1）如果三个数ａ，G，ｂ成等比数列，则G叫作ａ，ｂ的等比中项，那么如何用ａ，ｂ表示G呢？这个式子是三个数ａ，G，ｂ成等比数列的什么条件？

（2）在直角坐标系中，画出通项公式为ａn＝2n的数列的图像和函数y＝2x－1的图像．对比一下，你发现了什么？

（3）已知数列｛ａn｝满足ａn－ａn－1＝2n（ｎ≥2），数列｛bn｝满足，你会求它们的通项公式吗？

五、回顾反思

1. 在这节课上，你有哪些收获？

2. 你能用几个概念、几个公式来概括等比数列的有关内容吗？试试看．

点　评

这是一节典型的类比教学的案例，这节课的内容与等差数列的内容和研究方法非常相似，但设计者从类比入手，让学生亲自去发现，猜想，解决，无论从问题的提出，还是在解决方式、细节的处理上，和上节均有较大不同．相信这节课除了使学生可以更加熟练地掌握等差数列、等比数列的有关知识及常用的解题思想方法外，对类比思想的运用还会有所感悟和体会．

美中不足的是，等比数列的现实模型比较多，而这篇案例在对比方面的运用略显单薄．