2021学年25.4 相似三角形的判定课文课件ppt

这是一份2021学年25.4 相似三角形的判定课文课件ppt，共15页。PPT课件主要包含了全等三角形知多少，只考虑角，只考虑边，考虑部分角与部分边，1“角”等内容，欢迎下载使用。
沪科数学九年级（上册）　　
§24.2 相似三角形的判定　（一）
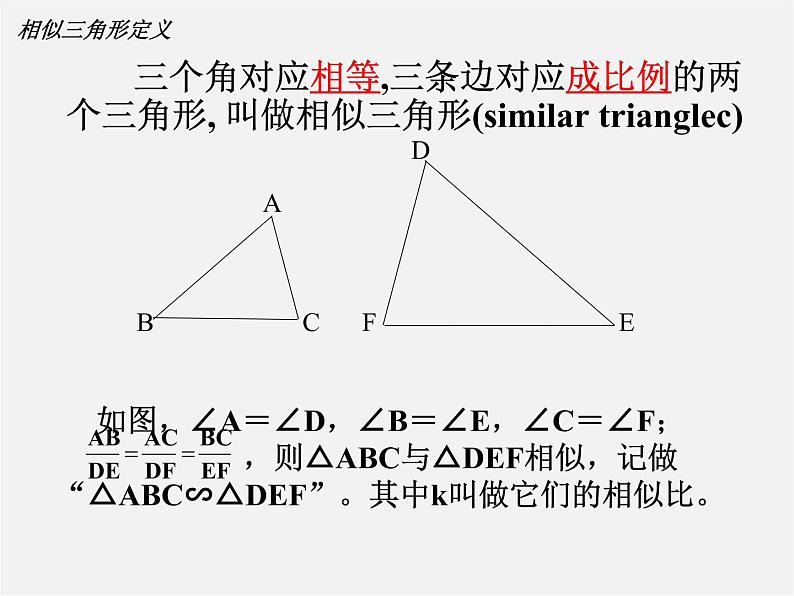
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形(similar trianglec)
如图，∠A＝∠D，∠B＝∠E，∠C＝∠F； ，则△ABC与△DEF相似，记做“△ABC∽△DEF”。其中k叫做它们的相似比。
思考：如果k＝1，这两个三角形有怎样的关系？
注意：要把表示对应角顶点的字母写在对应的位置上. 反之,写在对应位置上的字母就是对应角的顶点！
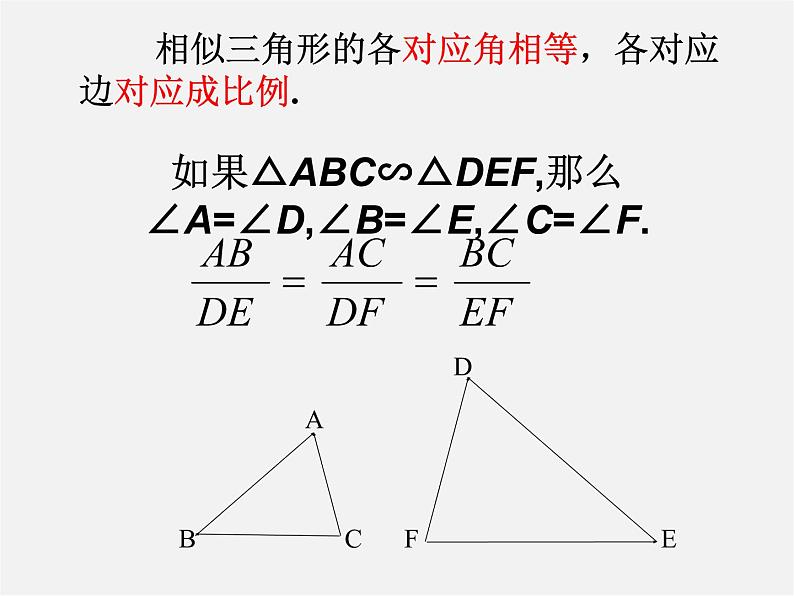
如果△ABC∽△DEF,那么 ∠A=∠D,∠B=∠E,∠C=∠F.
相似三角形的各对应角相等，各对应边对应成比例.
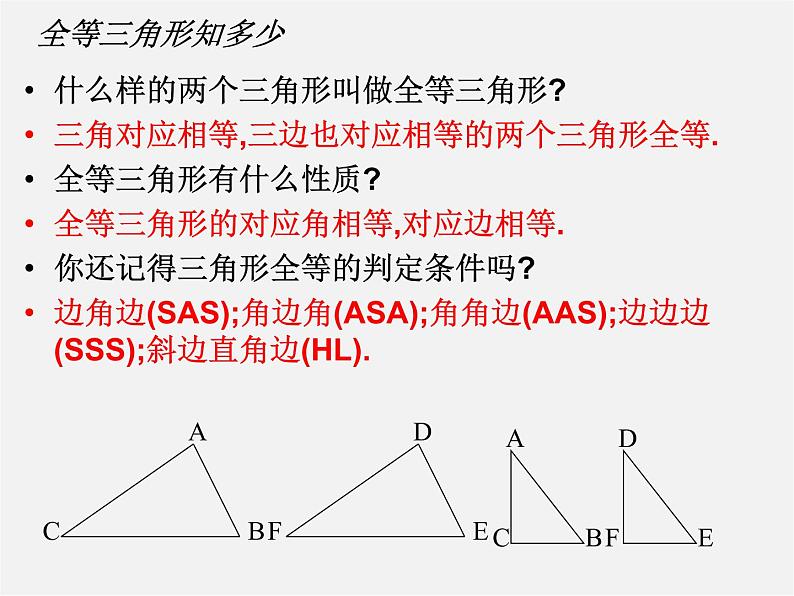
什么样的两个三角形叫做全等三角形?三角对应相等,三边也对应相等的两个三角形全等.全等三角形有什么性质?全等三角形的对应角相等,对应边相等.你还记得三角形全等的判定条件吗?边角边(SAS);角边角(ASA);角角边(AAS);边边边(SSS);斜边直角边(HL).
三角形相似的条件的探索方向
“各角对应相等、各边对应成比例的两个多边形相似”
是两多边形相似的定义与判定方法.
“三角对应相等、三边对应成比例的两个三角形相似”仍沿用了两多边形相似的定义与判定, 根本没有显示出“三角形是多边形的特殊情形”。
也就是边按一定的比例放大或缩小, 而角的大小与边的长短无关, 所以类比三角形全等可知…
［探究］1、在△ABC中，D为AB的中点，如图2，过D点作DB∥BC交AC于点E，那么△ADE与△ABC相似吗？
（2）“边”： 要证明对应边的比相等，有哪些方法？
Ⅰ、 直接运用三角形中位线定理及其逆定理
Ⅱ、利用全等三角形和平行四边形知识 过点D作DF∥AC交BC于点F，如图．
2、当D1、D2为AB的三等分点，如图4．过点D1、D2分别作 BC的平行线，交AC于点E1、E2，那么△AD1E1、△AD2E2与△ABC相似吗？
［猜想］3、 通过上面两个特例，可以猜测：当D为AB上任一点时，如图，过D点作DE∥BC交AC于点E，都有△ADE与△ABC．
［归纳］ 定理 平行于三角形一边的直线与其他两边（或两边的延长线）相交，截得的三角形与原三角形相似．
[操作]：课本第53～54页练习1、3
小结 内容总结 方法归纳
作业： 课本第53～54页 练习2． 《基础训练》第41～42页 练习2、3．
思考题： 如图、过 △ABC的边AB上任意一点D，作DE∥BC交AC于点E，那么